ou un peu d’analyse numérique…
L’apothème et le côté
La question était celle-ci, posée par un élève de deuxième secondaire,
Quel est le périmètre du polygone régulier dont l’angle extérieur en chaque sommet mesure environ 6,1˚ et dont le côté mesure 6,1 cm ?
L’apothème de ce polygone est-il plus grand ou plus petit que le côté ?
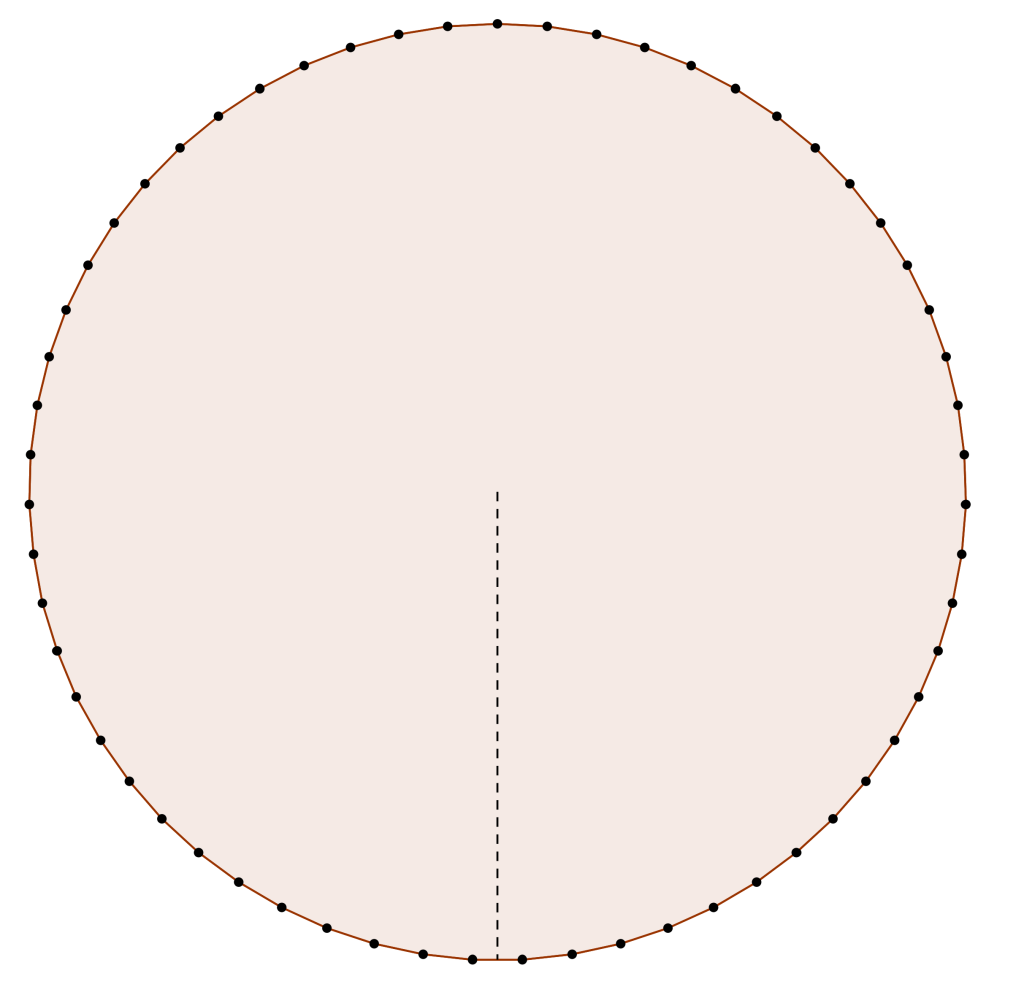
En deuxième secondaire, en utilisant le fait que l’angle extérieur a pour mesure 6,1° et en trouvant que ce polygone régulier comporte 59 côtés, on déduit intuitivement que la mesure de l’apothème est sans doute plus grande que celle du côté (la trigonométrie est enseignée deux ans plus tard). Le polygone régulier à 59 côtés, illustré ci-dessus, est pratiquement déjà indistinguable d’un cercle à l’œil nu.
D’autre part, on sait que l’apothème d’un triangle équilatéral est plus petit que son côté – en fait, même la hauteur est plus petite que son côté. Avec Pythagore, on peut trouver une expression qui représente la hauteur (qui est aussi une médiane) :
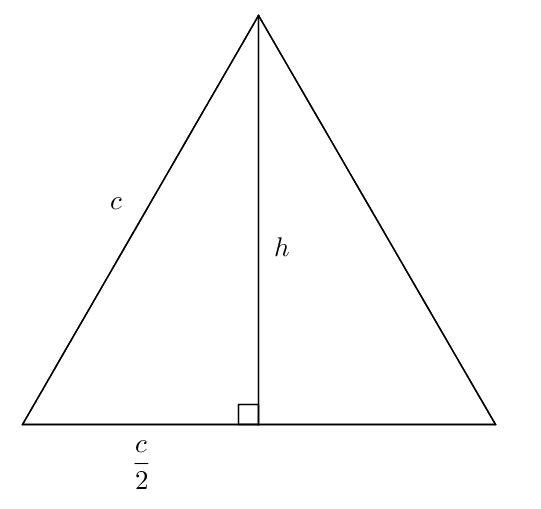
puis, par symétrie, 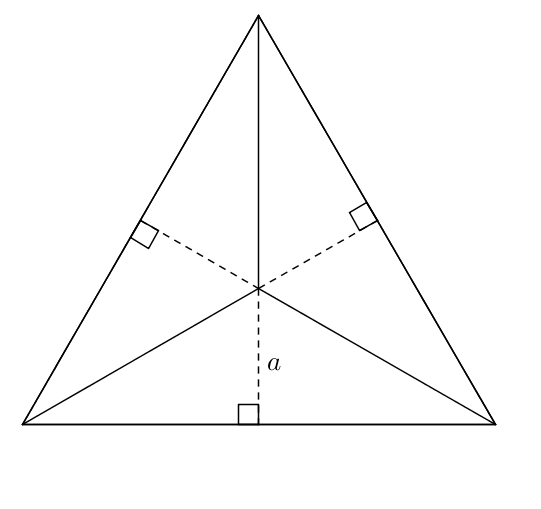
ou en utilisant le fait que les médianes se rencontrent au
On peut donc se demander quand le changement s’opère-t-il ? À partir de combien de côtés est-ce que l’apothème d’un polygone régulier devient-il plus grand que le coté de ce même polygone ?
En divisant le polygone régulier en 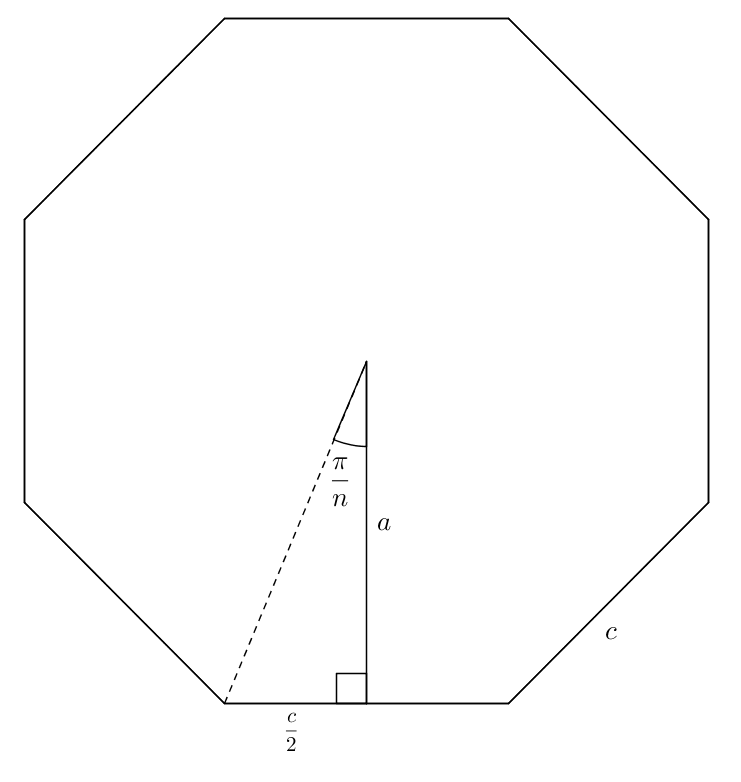
on pose
On cherche à résoudre l’inéquation
et en divisant par
Or
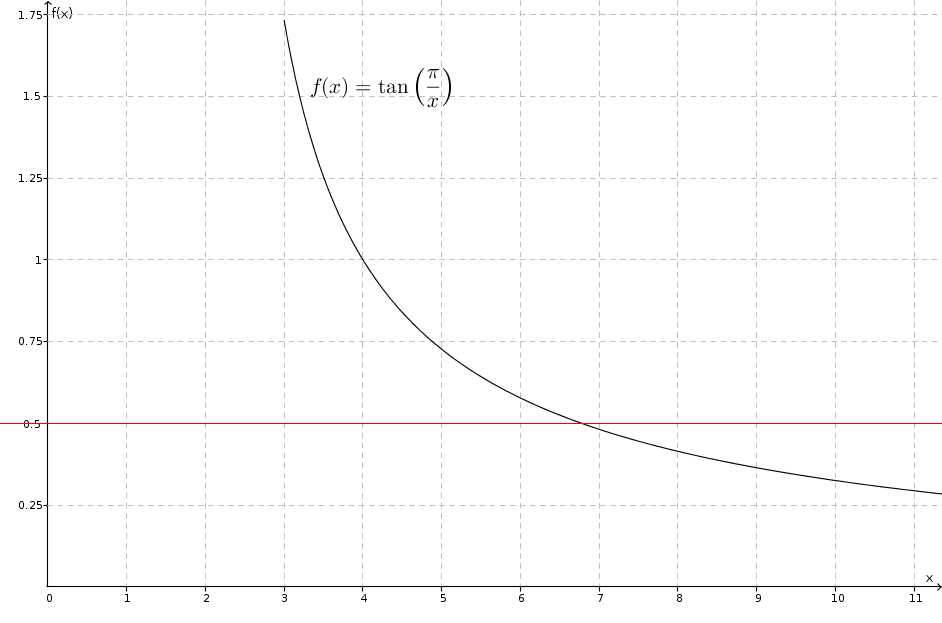
et on se rend compte que la mesure du côté du polygone régulier devient plus petite que l’apothème lorsqu’on passe de 6 à 7 côtés. Ainsi, pour le triangle équilatéral, le carré, le pentagone régulier et l’hexagone régulier, la mesure de l’apothème est plus petite que celle du côté ; pour l’heptagone régulier et les suivants, la mesure de l’apothème est plus grande que celle du côté.
Mieux vaut circonscrire… qu’inscrire
J’ai récemment donné à mes élèves le problème suivant :
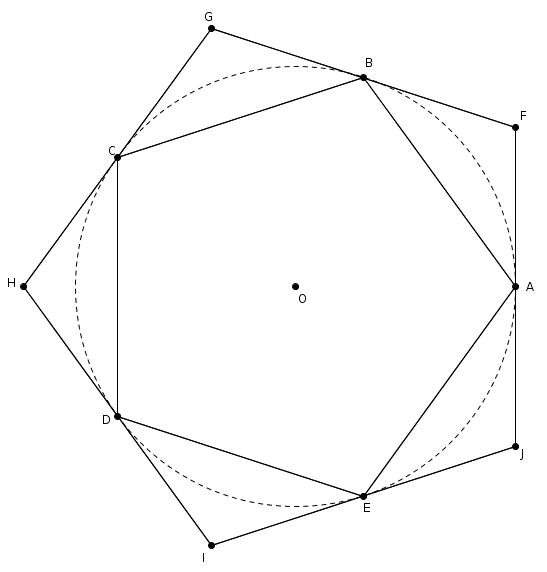
Dans le cercle suivant, on a inscrit le pentagone régulier
. La mesure d’un côté du pentagone est 542 cm. On a aussi tracé un deuxième pentagone régulier circonscrit au cercle. Les points , , , et sont respectivement les points milieux des côtés , , , et du pentagone .
Quel pentagone possède l’aire la plus proche de celle du disque ? Le pentagone
ou le pentagone ? note : J’ai choisi la mesure de 542 cm avec un bon vieux tableur : il s’avère qu’en utilisant la moitié de 542, c’est-à-dire 271, et la tangente, on peut trouver la mesure de l’apothème :
On est très près d’un entier… ça facilite la correction :-)
Bref, après quelques calculs, les élèves arrivaient à la conclusion que le pentagone régulier circonscrit avait une aire plus proche de l’aire du disque que le pentagone régulier inscrit.
Qu’en est-il des autres polygones réguliers ? Est-ce toujours le polygone circonscrit qui donne une meilleure approximation de l’aire du disque ? Voyons voir…
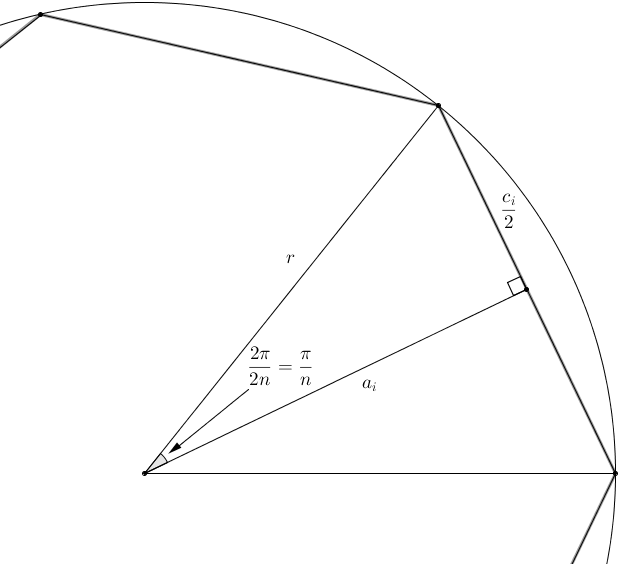 Si on pose
Si on pose 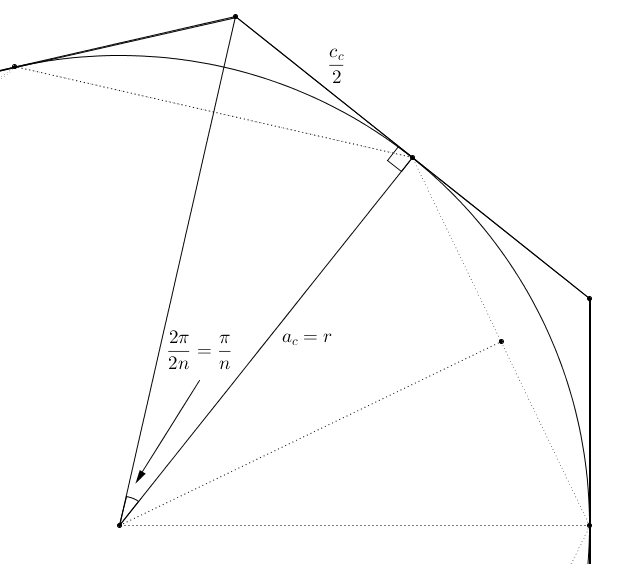
on a
Comme tous les disques et polygones réguliers à
Suspectant que le polygone circonscrit ait toujours une aire plus près de celle du disque que le polygone inscrit, c’est-à-dire que si
je me suis intéressé à la fonction suivante
Comme on ne considère que des valeurs de 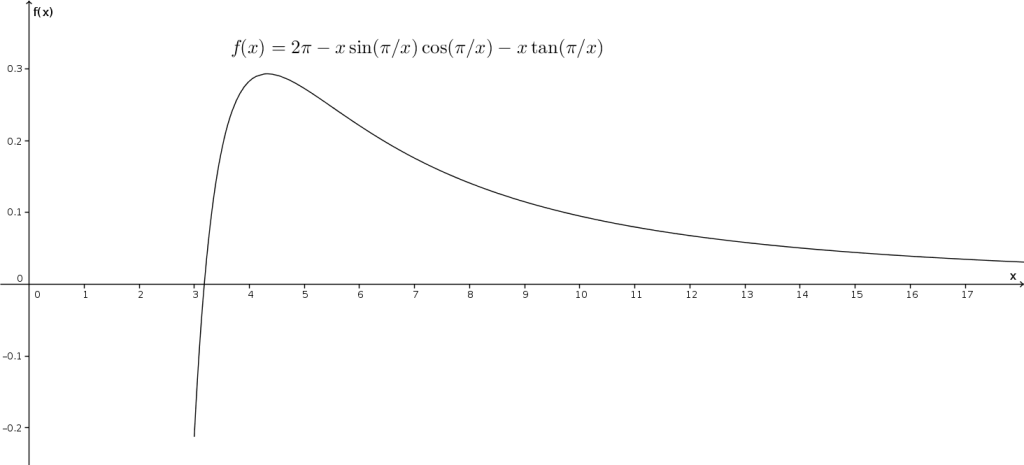
Or ce n’est pas le cas ! On voit que pour la valeur
À droite du zéro, la fonction reste gentiment au dessus de l’axe des abscisses (un petit exercice sur les limites suit).
No solutions exist. C’est WolframAlpha qui le dit !
Le terme
En d’autres mots, le polygone régulier circonscrit a toujours une aire plus proche de celle du disque que le polygone régulier inscrit… sauf dans le cas du triangle équilatéral : le triangle équilatéral inscrit à une aire plus proche de celle du disque que le triangle équilatéral circonscrit.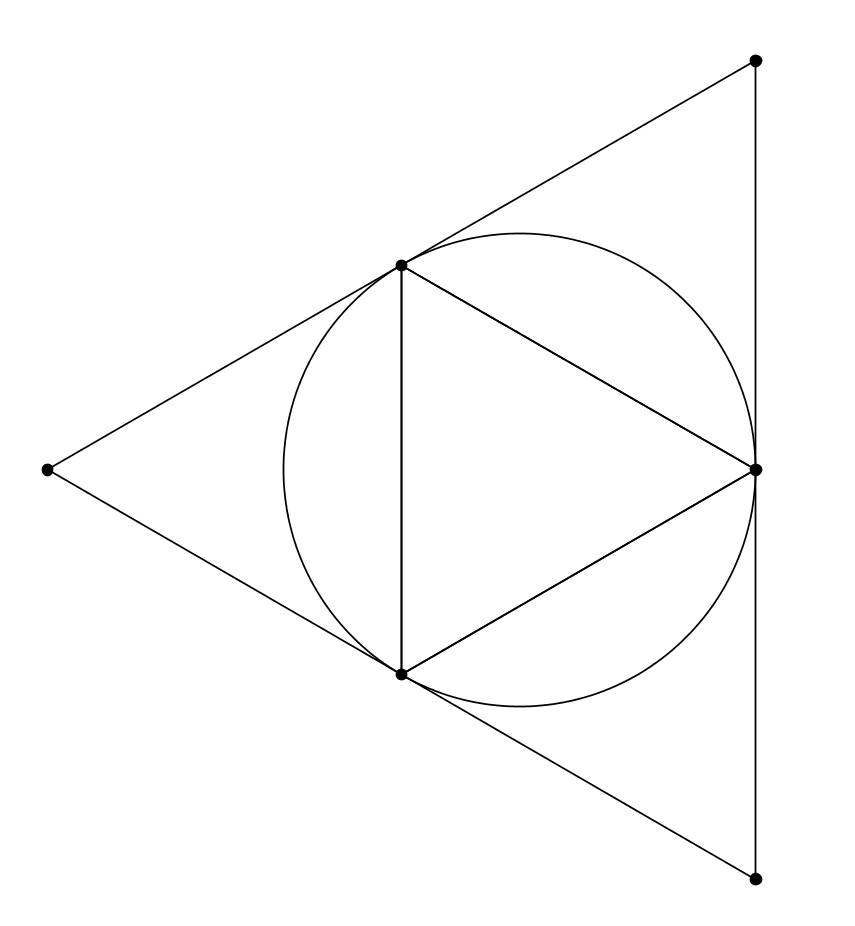
Bonjour, petite question concernant le logiciel utilisé ici… pourriez-vous me contacter par courriel? Merci!
C’est fait !