Grâce notamment aux logiciels de géométrie dynamique, il est tout à fait remarquable de faire découvrir aux élèves que dans n’importe quel triangle, le plus grand côté est toujours opposé au plus grand angle et le plus petit côté au plus petit angle.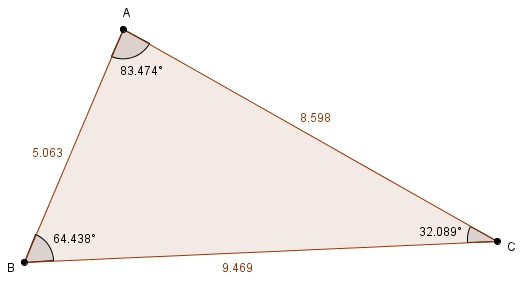
Il est intéressant, à ce moment, de se demander si les côtés opposés et leurs angles respectifs sont dans le même rapport : en d’autres mots, est-ce qu’on \[\frac{a}{\angle A} \overset{?}{=} \frac{b}{\angle B} \overset{?}{=} \frac{c}{\angle C}\]La réponse est bien entendue négative. En réalité, les côtés opposés sont proportionnels non pas aux angles mais aux sinus des angles. C’est la loi des sinus \[\frac{a}{\sin\left(\angle A\right)} = \frac{b}{\sin\left(\angle B\right)} = \frac{c}{\sin\left(\angle C\right)}\]La question est :
Que représente ce rapport entre les côtés opposés et les sinus des angles ?
Avant d’y répondre, et à des fins de complétude pour ce blogue, voici la preuve « cassique » de la loi des sinus telle que vue généralement en quatrième secondaire. Dans un triangle \(ABC\), on trace la hauteur \(CD\) que l’on nomme \(h\).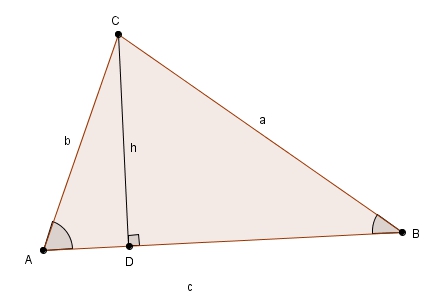
On a d’une part, dans le triangle \(ACD\),\[\sin\left(\angle A\right) = \frac{h}{b} \quad \Rightarrow \quad h = b\sin\left(\angle A\right)\]et, d’autre part, dans le triangle \(BCD\), \[\sin\left(\angle B\right) = \frac{h}{a} \quad \Rightarrow \quad h = a\sin\left(\angle B\right)\]En comparant les expressions obtenues pour la hauteur, on a \[a \sin\left(\angle B\right) = b\sin\left(\angle A\right)\]ou de manière équivalente \[\frac{a}{\sin\left(\angle A\right)} = \frac{b}{\sin\left(\angle B\right)}\]et la preuve est essentiellement complète puisqu’il est possible de répéter la manœuvre avec la hauteur relative au côté \(c\) et par transitivité, on obtient le résultat attendu. La démarche est la même si l’angle est obtus
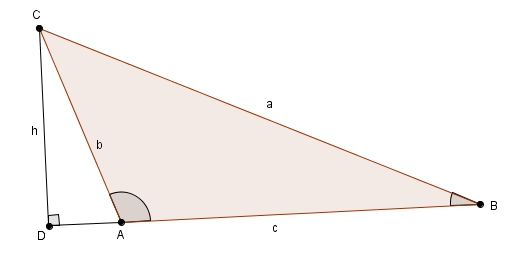puisque dans ce cas, les angles \(CAD\) et \(CAB\) sont supplémentaires et les sinus d’angles supplémentaires sont égaux \[\sin\left(\angle CAD\right) = \sin\left(180^{\circ}-\angle CAD\right)\]Ainsi on a \[\sin\left(\angle CAD\right) = \sin\left(\angle CAB\right)\]
Que représente ce rapport ?
Maintenant, pour répondre à la question, on considère un triangle \(ABC\) et son cercle circonscrit de centre \(O\). On trace le diamètre \(CD\).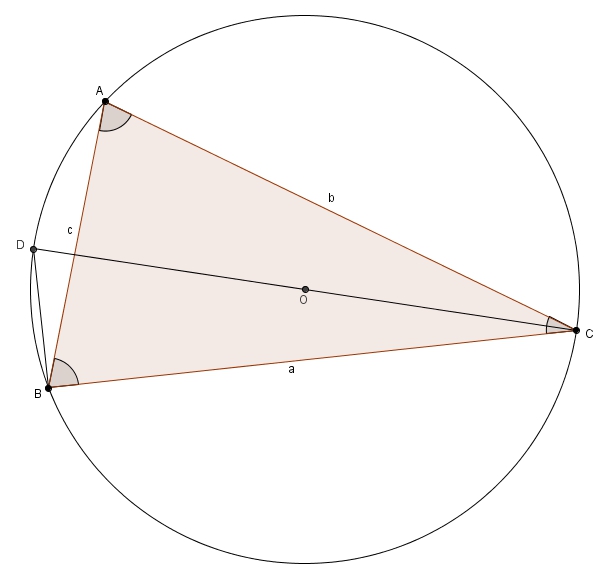
On pose le rayon égal à \(r\). En d’autres mots, m\[m\overline{CD} =2r\]L’angle \(CBD\) est droit puisque le triangle \(CBD\) est inscrit dans un cercle et l’un de ses côtés est un diamètre. On a donc \[\sin\left(\angle D\right) = \frac{a}{m\overline{CD}} = \frac{a}{2r}\]Or, les angles \(D\) et \(A\) sont isométriques puisqu’ils interceptent le même arc. En substituant, on obtient \[\sin\left(\angle A\right) = \frac{a}{2r}\]ou de manière équivalente \[2r = \frac{a}{\sin\left(\angle A\right)}\]En procédant de façon analogue, en considérant les autres angles, on obtient (le cercle circonscrit au triangle étant unique) \[2r = \frac{b}{\sin\left(\angle B\right)}\]et \[2r = \frac{c}{\sin\left(\angle C\right)}\]et donc \[2r = \frac{a}{\sin\left(\angle A\right)} = \frac{b}{\sin\left(\angle B\right)} = \frac{c}{\sin\left(\angle C\right)}\]ce qui complète la preuve. On sait maintenant que le rapport constant entre les côtés opposés et les sinus des angles dans la loi des sinus est égal au diamètre du cercle circonscrit ! Et encore une fois, si le triangle est obtusangle, comme dans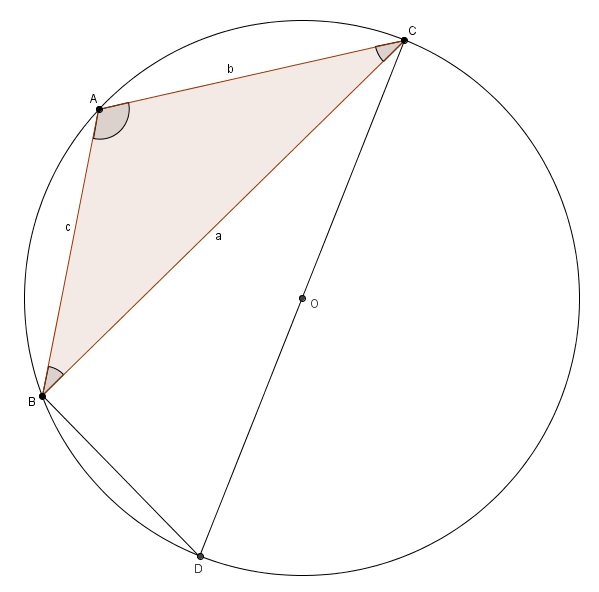
alors pas de problème ! Les angles \(A\) et \(D\) sont supplémentaires puisqu’ils sont des angles opposés dans un quadrilatère inscrit dans un cercle (Proposition III.22 des Éléments d’Euclide). Et comme les sinus d’angles supplémentaires sont égaux, on a bien \[\sin\left(\angle D\right) = \sin\left(\angle A\right)\]
Belle démonstration mais elle s’effondre si on supprime le dessin.
On n’a pas besoin de passer par un angle aigu pour calculer le sinus d’un angle obtu
Vous avez pu démontrer la lois des sinus (à la fin) on se passant de la relation établie au début ( l’égalité des rapports sans donner leur valeur commune)
Derniere remarque , dans un triangle les angles sont moindre que l’angle plat. Leur sinus est donc positif (cercle trigonométrique) et se calcule de la même façon qu’un angle aigu ce qui n’est pas vrai pour le calcul du cosinus
Merci d’avoir soulevé ce problème de démonstration se basant sur la figure géométrique)
Salut wafi,
d’abord merci du commentaire. Je ne comprend pas exactement qu’est-ce qui pourrait s’effondre. Dans la première partie, si on a vu le cercle trigonométrique, alors oui, effectivement, la remarque concernant les sinus d’angles supplémentaires est, à la rigueur, superflue (mais pas fausse), puisqu’on sait que
h = b * sin(A)
que A soit aigu ou obtus. Cette (première) démonstration s’inscrivait davantage dans un contexte de rapport trigonométrique dans le triangle rectangle
sin(A) = cathète opposée / hypoténuse
Les élèves travaillent avec des triangles rectangles pendant un moment et dans lesquels l’angle A est toujours aigu. Qu’arrive-t-il dans les triangles non-rectangles ? C’est dans ces cas-là qu’on voit la loi des sinus (et la loi des cosinus). Or un triangle non-rectangle peut être obtusangle, et il faudra éventuellement considérer un sinus d’angle obtus bien qu’à partir de notre définition (de rapport trigonométrique, pas du sinus dans le cercle) cela semble aberrant : on leur montre alors que pour être cohérent, on a bien la relation suivante
sin(A) = sin(180° – A)
et la loi des sinus tient pour les triangles obtusangles. Lorsque les élèves voient le cercle trigonométrique alors cette propriété prend encore plus de sens…
Pour la deuxième preuve, la remarque sur les sinus d’angles supplémentaires m’apparaît essentielle puisque les angles A et D n’interceptent pas les mêmes arcs comme c’est le cas lorsque l’angle est aigu.
Au plaisir,
Bonsoir
Pour votre premiere question, ne regarder ,ni se representer mentalement la figure géométrique et voir si vous pouvez donner les résultats ou distinguer le cas d’un angle obtu!!??(comme pour un calcul algébrique)
Cordialement
Bonsoir wafi,
je ne vois pas l’intérêt, dans un problème de géométrie, de “ne regarder ,ni se representer mentalement la figure géométrique”. Au contraire, je crois que réfléchir en toute rigueur à l’aide d’un support visuel juste est même parfaitement adéquat (je ne veux pas non plus radoter sur les vieux trucs des schémas erronés, les années ’60 sont finies).
Malgré cela, même sans figure, il faut être capable lorsqu’on pose un problème de considérer les différentes avenues. Parfois ces différentes avenues mènent à la même démarche “algébrique” et parfois non (comme dans la deuxième preuve du billet). Et parfois on peut s’accommoder d’une convention et regrouper sous une même démarche “algébrique” les différentes avenues : je donne comme exemple en géométrie la convention des mesures signées de segments. Parfois non.
Dans le cas spécifique, et je considère que vous avez pris compte du contexte dans lequel je vois cette preuve avec les élèves, dans un triangle ABC, si l’angle A est obtus, alors la hauteur issue de C tombe à l’extérieur du triangle, sur le prolongement de AB. C’est le triangle rectangle ACD que l’on considère qui possède l’angle aigu que l’on utilise pour poser le rapport trigonométrique et cet angle n’est pas l’angle A du triangle ABC initial. L’expression
sin(A) = h/b
n’a donc aucun sens à ce moment. Il faut donc spécifier que les sinus de ces deux angles (supplémentaires) sont égaux afin d’énoncer la loi des sinus.
Bonne soirée,
The Dude
Bonjour
Parfaitement d’accord axvec vous si on s’adresse à des élèves du collège ou lycée et si notre objectif est uniquement la formule recherchée.
Si on veut étendre l’objectif, ( comme vous avez étendu la lois des sinus) au delà de la démonstration de cette lois, aux problèmes et obstacles que rencontrent les élèves en mathématiques et particulierement en géométrie et qui sont liés principalement à la démonstration ( bete noire des élèves), alors la figure géométrique est l’un des piliers de la démonstration et c’est essentiel d’habituer les élèves à y recourir mais avec prudence (je ne pense pas qu’un élève peut envisager les deux cas comme vous l’avez fait s’il ne pense pas à distinguer les cas . Chose qui se base sur un raisonnement independemment de la fig geo.
A ce propos, j’ai un exercice de géométrie au collège, dont la construction de la fig geo qui va aider à démontrer le résultat demandé, démontre ce résultat. Je vous l’enverrai prochainement.
Bonne journée
Bonjour wafi,
“c’est essentiel d’habituer les élèves à y recourir mais avec prudence (je ne pense pas qu’un élève peut envisager les deux cas comme vous l’avez fait s’il ne pense pas à distinguer les cas .”
je n’aurais pas pu mieux le dire. Et je suis tout à fait d’accord avec vous concernant les difficultés inhérantes à l’enseignement (à l’apprentissage) de la preuve.
Bonne journée à vous aussi et bon courage !
Bonsoir
J’ai pensé que ce lien peut vous interesser
http://www.slate.fr/lien/60005/maths-matiere-inutile
Bonjour wafi,
merci pour le lien. La question de l’enseignement des mathématiques est profonde et épineuse. La communauté des enseignants de mathématiques sur le web est fort heureusement très riche en réflexions, en échanges et en partage.
Je peux cependant vous assurez (si cela vous rassure !) que mes cours ne ressemblent pas du tout à mon blog !
Bonne journée !
The Dude
Bonsoir
Vous dites que vos cours ne ressemblent pas à votre blog mais comment un lecteur ( non averti) peut il prendre ses précautions surtout si c’est un enseignant débutant?
Bonne nuit
Bonjour,
j’écris ce blogue d’abord pour moi, pour y confiner et conserver quelques résultats que je trouve intéressants dans un format que je trouve plaisant. Les lecteurs peuvent y trouver ce qu’ils veulent. Sauf à de rares exceptions, et c’est assez clair je crois, je m’autorise rarement des prétentions ou des remarques pédagogiques. Peut-être ces remarques prendront-elles éventuellement davantage de place mais ce n’est pas pour l’instant le but de ce blogue.
Tres bonne idée. Bon courage.
Personnellement j’ai beaucoup de reflexions concernant l’apprentissage et l’enseignement des maths ainsi que sur la formation des enseignants et des inspecteurs de maths mais je remets leur enregistrement à plus tard. Je ne le fais que RAREMENT. Votre idée est fort intéressant.
Bonne fin de journée