Valeurs exactes

Grâce à la relation de Pythagore et à quelques triangles rectangles bien choisis, il est facile de calculer les valeurs exactes de certains rapports trigonométriques.  Les classiques $$\sin ({30}^{\circ })=\cos ({60}^{\circ })=\frac{1}{2}$$ou $$\sin ({45}^{\circ })=\cos ({45}^{\circ })=\frac{\sqrt{2}}{2}$$ou encore $$\sin ({60}^{\circ })=\cos ({30}^{\circ })=\frac{\sqrt{3}}{2}$$peuvent être trouvés de cette façon.  Puis, avec les formules d’addition d’angles et d’angles doubles, on peut trouver d’autres valeurs exactes.   Par exemple, en se rappelant que $$\sin (\alpha +\beta )=\sin (\alpha )\cos (\beta )+\sin (\beta )\cos (\alpha )$$on peut trouver $$\sin ({30}^{\circ }+{45}^{\circ })=\sin ({30}^{\circ })\cos ({45}^{\circ })+\sin ({45}^{\circ })\cos ({30}^{\circ })$$Et en remplaçant par ce qui est connu, on obtient $$\sin ({75}^{\circ })=\frac{1}{2}\cdot \frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{3}}{2}$$ce qui fait $$\sin ({75}^{\circ })=\frac{\sqrt{2}}{4}+\frac{\sqrt{6}}{4}$$ou si on préfère $$\begin{array}{rl}\sin ({75}^{\circ })& =\frac{\sqrt{2}+\sqrt{6}}{4}\\ \\ & =\frac{\sqrt{2}(1+\sqrt{3})}{4}\end{array}$$Ou bien, en se rappelant que $$\cos (2\alpha )=2{\cos }^2(\alpha )-1$$on trouve $$\cos (2\cdot {15}^{\circ })=2{\cos }^2({15}^{\circ })-1$$ce qui fait $$\cos ({30}^{\circ })=2{\cos }^2({15}^{\circ })-1$$En remplaçant la valeur du cosinus connue, on obtient $$\frac{\sqrt{3}}{2}=2{\cos }^2({15}^{\circ })-1$$On additionne $1$ de chaque côté $$\frac{\sqrt{3}}{2}+1=2{\cos }^2({15}^{\circ })$$ce qui fait $$\frac{\sqrt{3}}{2}+\frac{2}{2}=2{\cos }^2({15}^{\circ })$$et donc $$\frac{\sqrt{3}+2}{2}=2{\cos }^2({15}^{\circ })$$Puis en divisant chaque côté de l’équation par $2$ $$\frac{\sqrt{3}+2}{4}={\cos }^2({15}^{\circ })$$Il suffit enfin d’extraire la racine carrée de chaque côté de l’équation (on note que $\cos ({15}^{\circ })$ est positif) $$\sqrt{\frac{\sqrt{3}+2}{4}}=\cos ({15}^{\circ })$$ce qui fait $$\frac{\sqrt{\sqrt{3}+2}}{\sqrt{4}}=\cos ({15}^{\circ })$$et donc plus simplement $$\frac{\sqrt{\sqrt{3}+2}}{2}=\cos ({15}^{\circ })$$Et comme $$\sin ({75}^{\circ })=\cos ({15}^{\circ })$$on obtient ce joli résultat $$\frac{\sqrt{6}+\sqrt{2}}{4}=\frac{\sqrt{\sqrt{3}+2}}{2}$$ $$\frac{\sqrt{6}+\sqrt{2}}{4}=\frac{2\sqrt{\sqrt{3}+2}}{4}$$ $$\sqrt{6}+\sqrt{2}=2\sqrt{\sqrt{3}+2}$$

Bon.  Tout cela reste cependant bien peu spectaculaire.  Voici un résultat différent qui, en général, ne manque pas d’impressionner les étudiants.  Trouvons la valeur exacte de $\cos ({36}^{\circ })$. Exit les triangles rectangles.  Nous allons considérer le triangle isocèle suivant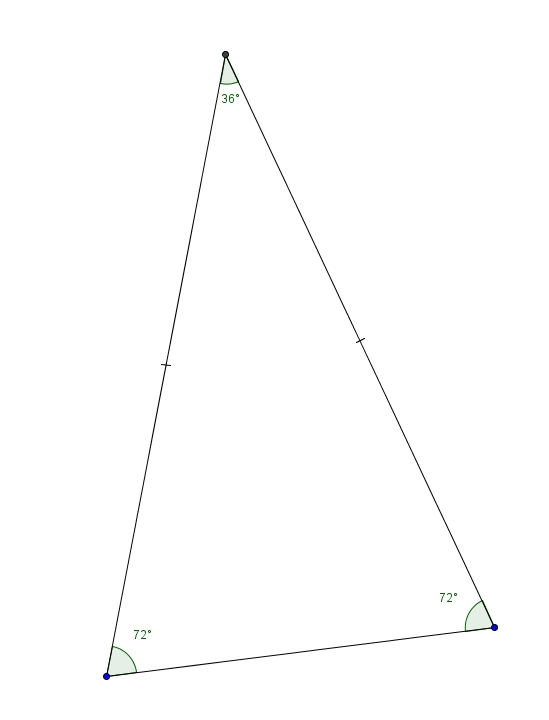On appelle ce triangle le triangle d’or.  Si on trace la bissectrice d’un des angles de ${72}^{\circ }$, on obtient un nouveau triangle isocèle semblable au premier (cas de similitude AA).  On peut répéter le processus indéfiniment.  Ceux qui connaissent le rectangle d’or y voient l’analogie.

Traçons, justement, une de ces bissectrices.  On obtient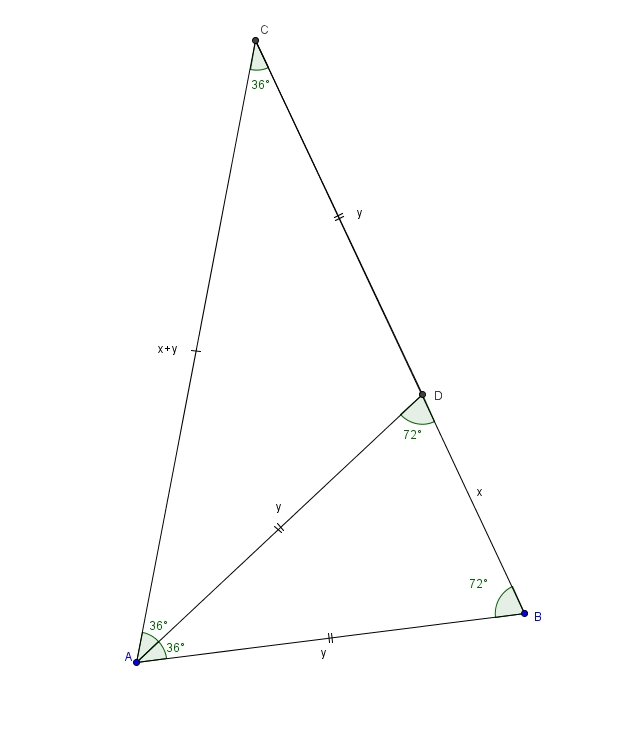

Le triangle $ABD$ est semblable au triangle $ABC$ par AA.  Le triangle $ABD$ est isocèle.  Si $\overline{AB}$ mesure $y$, alors $\overline{AD}$ aussi puisque ce sont les côtés isométriques du triangle isocèle.  Mais il y a en un troisième, triangle isocèle, bien qu’il ne soit pas semblable aux deux autres.  C’est le triangle $ADC$ (observez la paire d’angles de ${36}^{\circ }$).  On trouve ainsi que la mesure de $\overline{DC}$ est aussi égale à $y$.  En posant la mesure de $\overline{BD}$ égale à $x$, on trouve que la mesure de $\overline{BC}$ (et donc aussi de $\overline{AC}$) est égale à $x+y$.  On peut établir la proportion suivante en associant correctement les côtés homologues dans les deux triangles semblables $$\frac{m\overline{BD}}{m\overline{AB}}=\frac{m\overline{AB}}{m\overline{BC}}$$ ou plus simplement $$\frac{x}{y}=\frac{y}{x+y}$$En effectuant le produit croisé, on obtient $$x^2+xy=y^2$$On divise ensuite chaque côté par $x^2$ $$\frac{x^2}{x^2}+\frac{xy}{x^2}=\frac{y^2}{x^2}$$ce qui fait $$1+\frac{y}{x}={\left(\frac{y}{x}\right)}^2$$On obtient ainsi un polynôme du deuxième degré en $\frac{y}{x}$ $${\left(\frac{y}{x}\right)}^2-\frac{y}{x}-1=0$$Avec la formule quadratique, on trouve $$\frac{y}{x}=\frac{-(-1)\pm \sqrt{(-1{)}^2-4\cdot 1\cdot (-1)}}{2\cdot 1}$$Comme $\frac{y}{x}$ est un rapport de mesures positives, on ne retient que la valeur positive pour $\frac{y}{x}$ $$\frac{y}{x}=\frac{1+\sqrt{1+4}}{2}$$ce qui fait $$\frac{y}{x}=\frac{1+\sqrt{5}}{2}$$On reconnait d’ailleurs le nombre d’or.  Pour des raisons à ce moment loin d’être apparentes, on fait deux choses : d’abord on inverse et puis on élève au carré.  On obtient dans un premier temps $$\frac{x}{y}=\frac{2}{1+\sqrt{5}}$$En rationalisant le dénominateur on obtient $$\begin{array}{rl}\frac{x}{y}& =\frac{2}{1+\sqrt{5}}\\ \\ & =\frac{2}{1+\sqrt{5}}\cdot \frac{1-\sqrt{5}}{1-\sqrt{5}}\\ \\ & =\frac{2(1-\sqrt{5})}{-4}\end{array}$$ce qui fait en simplifiant le dénominateur $$\frac{x}{y}=\frac{-1+\sqrt{5}}{2}$$Sitôt ce résultat obtenu, on élève au carré $${\left(\frac{x}{y}\right)}^2={\left(\frac{-1+\sqrt{5}}{2}\right)}^2$$ce qui est équivalent à $${\left(\frac{x}{y}\right)}^2=\frac{{(-1+\sqrt{5})}^2}{2^2}$$En développant $${\left(\frac{x}{y}\right)}^2=\frac{1-2\sqrt{5}+5}{4}$$et en regroupant les termes semblables $${\left(\frac{x}{y}\right)}^2=\frac{6-2\sqrt{5}}{4}$$Finalement, en simplifiant la fraction, on obtient $${\left(\frac{x}{y}\right)}^2=\frac{3-\sqrt{5}}{2}$$Considérons maintenant l’angle BAD de 36° dans le triangle BAD.  En utilisant la loi des cosinus, on peut écrire $$x^2=y^2+y^2-2\cdot y\cdot y\cdot \cos ({36}^{\circ })$$En simplifiant le membre de droite on obtient $$x^2=2y^2-2y^2\cos ({36}^{\circ })$$On effectue d’abord la mise en évidence du carré de $y$ à droite $$x^2=y^2(2-2\cos ({36}^{\circ }))$$puis on divise chaque côté par ce même carré de $y^2$ $$\frac{x^2}{y^2}=2-2\cos ({36}^{\circ })$$Il nous suffit donc d’écrire $${\left(\frac{x}{y}\right)}^2=2-2\cos ({36}^{\circ })$$pour comprendre la peine qu’on s’était donnée pour trouver $${\left(\frac{x}{y}\right)}^2=\frac{3-\sqrt{5}}{2}$$On obtient donc $$\frac{3-\sqrt{5}}{2}=2-2\cos ({36}^{\circ })$$Il suffit maintenant d’isoler sans trop de mal le cosinus.  On divise chaque côté par $2$ $$\frac{3-\sqrt{5}}{4}=1-1\cos ({36}^{\circ })$$On soustrait ensuite $1$ de chaque côté $$\frac{3-\sqrt{5}}{4}-1=-\cos ({36}^{\circ })$$ce qui fait $$\frac{3-\sqrt{5}}{4}-\frac{4}{4}=-\cos ({36}^{\circ })$$et donc en effectuant la soustraction $$\frac{-1-\sqrt{5}}{4}=-\cos ({36}^{\circ })$$On multiplie enfin chaque côté de l’égalité par $-1$ $$\frac{1+\sqrt{5}}{4}=\cos ({36}^{\circ })$$Voilà ! La valeur exacte du cosinus de ${36}^{\circ }$.