Élève : Je voulais savoir si ce que j’avais fait est bon.
Collègue : Bien sûr ! Que devais-tu faire ?
É : Je devais diviser \(\frac{21}{8}\) par \(\frac{7}{4}\).
C : \(\frac{21}{8}\div \frac{7}{4}\) Bien ! Qu’as-tu fait ?
É : Comme on avait \[\frac{21}{8}\div \frac{7}{4}\]à faire, j’ai divisé \(21\) par \(7\) puis j’ai divisé \(8\) par \(4\) et j’ai obte…
C : Oups ! Je t’arrête ! Tu t’es trompé ! Tu as sûrement confondu la multiplication avec la division ? Quand on multiplie des fractions, on multiplie les numérateurs ensemble et on multiplie les dénominateurs ensemble. Vrai. Mais pour la division, on ne peut pas faire ça ! On doit exprimer la division comme une multiplication par l’inverse.
É : Oh… Ok.
C : Puisque \(\frac{4}{7}\) est l’inverse de \(\frac{7}{4}\), on fait \begin{align*}\frac{21}{8}\div \frac{7}{4} &= \frac{21}{8}\times \frac{4}{7} \\ \\ &=\frac{21\times 4}{8\times 7} \\ \\ &=\frac{84}{56} \\ \\ &=\frac{84\div 28}{56 \div 28} \\ \\ &= \frac{3}{2}\end{align*}Voilà ! On obtient la fraction réduite \(\frac{3}{2}\).
É : Ah! Mais j’ai obtenu \(\frac{3}{2}\) moi aussi et c’était moins de travail !
C : Ah ? Ouin… mais… c’est un hasard ! Ça fonctionne avec ces nombres là mais c’est par chance. Avec d’autres nombres ça ne fonctionne pas.
Ce petit échange entre une collègue et son élève et dont j’ai été témoin m’a donné l’idée de ce billet dans lequel on traitera, on le devine, de la division de fractions (je ferme pour l’instant les yeux sur la multiplication qu’elle a proposée).
La division de fractions : à partir d’un support visuel
À l’école, plus jeune, on m’a introduit la division de fractions comme une multiplication par l’inverse, sans plus d’explication, sans motivation. Or, lorsqu’on fait l’effort d’essayer d’expliquer la division de fractions, de verbaliser le processus, il est plus commode de passer par un dénominateur commun que par la multiplication par l’inverse. À titre d’exemple, considérons la division suivante \[\frac{3}{5} \div \frac{2}{7}\]D’abord notons que \(\frac{3}{5}\) est supérieur à \(\frac{1}{2} = \frac{3}{6}\) et \(\frac{2}{7}\) est inférieur à \(\frac{1}{2}=\frac{2}{4}\). Ainsi, usant de l’interprétation « remplissage » de la division, \(\frac{2}{7}\) « rentre » au moins une fois dans \(\frac{3}{5}\) ce qui nous assure que le quotient sera supérieur à \(1\).
Si le rectangle est l’entier, on représente \(\frac{3}{5}\).

Chaque part représente \(\frac{1}{5}\) de l’entier, il y a \(3\) parts. Il est difficile de voir combien de paquets de \(2\) parts on peut faire car ces parts sont de tailles différentes ; dans ce cas-ci, on voudrait faire des paquets de \(2\) parts de \(\frac{1}{7}\) alors que les morceaux à notre disposition sont de \(\frac{1}{5}\). Solution ? Chercher des morceaux de la même taille. Cela revient, bien sûr, à trouver un dénominateur commun. Ici, si on divise chaque morceau en sept parts, on obtient \(35\) parts dans l’entier.
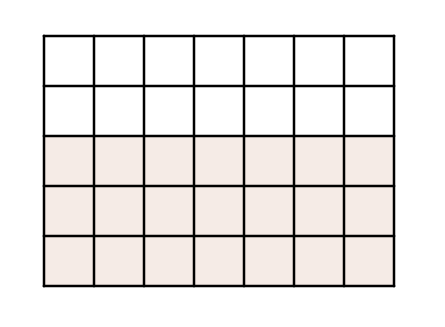
Il est facile de voir que nos \(3\) parts originales de \(\frac{1}{5}\) correspondent à \(21\) parts de \(\frac{1}{35}\), c’est-à-dire que \[\frac{3}{5} = \frac{21}{35}\]En outre, au lieu de chercher à faire des paquets de \(2\) parts de \(\frac{1}{7}\), on cherche maintenant à faire des paquets de \(10\) parts de \(\frac{1}{35}\), c’est-à-dire de \[\frac{2}{7} = \frac{10}{35}\]Si on s’exécute, on obtient
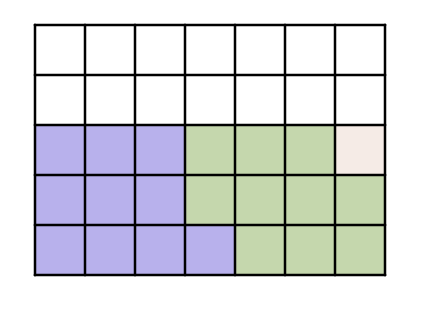
Clairement, je peux faire \(2\) paquets de \(\frac{10}{35}\), qui sont en bleu et en vert sur l’image, mais il reste une part seule à la fin. Comme on essaie de faire des paquets de \(10\) parts, celle-ci représente le \(\frac{1}{10}\) d’un troisième paquet. Ainsi, on peut écrire \begin{align*}\frac{3}{5} \div \frac{2}{7} &= \frac{21}{35} \div \frac{10}{35} \\ \\ &= \frac{21}{10} \\ \\ &=2\tfrac{1}{10}\end{align*}
On note que cela fonctionne aussi bien lorsque le quotient est inférieur à \(1\). On ne peut simplement pas former un paquet complet, seulement une fraction d’un paquet. Considérons \[\frac{2}{3} \div \frac{7}{8}\]On cherche à faire des paquets de \(7\) parts de \(\frac{1}{8}\) alors qu’on a \(2\) parts de \(\frac{1}{3}\). Comme les parts n’ont pas la même taille, c’est, bien sûr, pour l’instant, impossible. On obtient des parts de la même taille en divisant ceux-ci pour obtenir des parts de \(\frac{1}{24}\). Dans ce cas-ci, nos \(2\) parts de \(\frac{1}{3}\) deviennent \(16\) parts de \(\frac{1}{24}\) et nos \(7\) parts de \(\frac{1}{8}\) deviennent \(21\) parts de \(\frac{1}{24}\). Combien de paquets de \(21\) parts de \(\frac{1}{24}\) peut-on faire avec seulement \(16\) parts de \(\frac{1}{24}\) ? Même pas un ! En fait, on ne peut faire que le \(\frac{16}{21}\) d’un paquet. \begin{align*}\frac{2}{3}\div \frac{7}{8} &= \frac{16}{24} \div \frac{21}{24} \\ \\ &= \frac{16}{21}\end{align*}
La règle d’or
Conway et Guy, deux grands mathématiciens qui nous ont quitté récemment à quelques semaines d’intervalle, dans leur excellent livre The Book of Numbers [1], appelle la règle d’or celle qui nous permet d’obtenir des fractions équivalentes :
Si on multiplie ou divise le numérateur et le dénominateur d’une fraction par le même nombre, on obtient une fraction équivalente.
Les fractions \(\frac{4}{7}\) et \(\frac{20}{35}\) sont des fractions équivalentes car \[\frac{4}{7} = \frac{4\textcolor{Blue}{\, \times \, 5}}{7\textcolor{Blue}{\, \times \, 5}} = \frac{20}{35}\]Les fractions \(\frac{26}{39}\) et \(\frac{2}{3}\) sont un autre exemple de fractions équivalentes car \[\frac{26}{39} = \frac{26\textcolor{Blue}{\, \div \, 13}}{39\textcolor{Blue}{\, \div \, 13}} = \frac{2}{3}\]L’expérience nous assure que c’est exact : si on a quatre fois plus de parts mais que les parts sont quatre fois plus petites, ou si on a treize fois moins de parts, mais que les parts sont treize fois plus grosses… ça ne change rien !
Bien sûr, nous sommes tous familier avec cet aspect des fractions. La règle d’or porte son nom car elle nous permet d’effectuer toutes les opérations usuelles : \(+\), \(-\), \(\times\) et \(\div\).\begin{align*}\frac{2}{3} + \frac{1}{4}&= \frac{2\times 4}{3\times 4} + \frac{1\times 3}{4\times 3}\\ \\ &= \frac{8}{12} +\frac{3}{12} \\ \\ &= \frac{11}{12} \\ \\ \\ \frac{9}{11}-\frac{2}{3} &= \frac{9\times 3}{11\times 3}-\frac{2\times 11}{3\times 11} \\ \\ &=\frac{27}{33}-\frac{22}{33} \\ \\ &=\frac{5}{33} \\ \\ \\ \frac{1}{4} \times \frac{2}{3} &= \frac{1}{4}\times \frac{2\times 2}{3\times 2} \\ \\ &=\frac{1}{4}\times \frac{4}{6} \\ \\ &= \frac{1}{6}\end{align*}En examinant le dernier exemple, et sachant que \(\frac{1}{4}\times\) se traduit par \(\frac{1}{4}\) de… cela suggère une stratégie pour multiplier des fractions différente de celle expliquée par ma collègue plus haut. La multiplication de fractions fera d’ailleurs l’objet d’un billet à part entière.
Les fractions équivalentes
Ainsi, pour diviser des fractions, aucune technique particulière n’est nécessaire, si la règle d’or nous est familière et qu’on représente la fraction elle-même comme une division, comme en témoigne cet exemple dans lequel on divise \(\frac{2}{3}\) par \(\frac{5}{11}\) : \begin{align*}\frac{2}{3} \div \frac{5}{11} &= \frac{\phantom{a}\frac{2}{3}\phantom{a}}{\frac{5}{11}} \\ \\ &= \frac{\phantom{a}\frac{2}{3}\textcolor{Blue}{\, \times \, 11}\phantom{a}}{\frac{5}{11}\textcolor{Blue}{\, \times \, 11}}\\ \\ &= \frac{\phantom{a}\frac{22}{3}\phantom{a}}{5} \\ \\ &= \frac{\phantom{a}\frac{22}{3}\textcolor{Blue}{\, \times\, 3}\phantom{a}}{5\textcolor{Blue}{\, \times \, 3}}\\ \\ &= \frac{22}{15}\end{align*}
En mettant sur dénominateur commun et en divisant les numérateurs
Tel qu’expliqué ci-haut, il est possible d’exprimer le dividende et le diviseur avec des fractions équivalentes qui ont le même dénominateur. Ce faisant, on s’assure que les parts ont la même taille. Il suffit ensuite de diviser les numérateurs.\begin{align*} \frac{1}{8} \div \frac{3}{20} &= \frac{1\textcolor{Blue}{\, \times \, 5}}{8\textcolor{Blue}{\, \times \, 5}}\div \frac{3\textcolor{Blue}{\, \times \, 2}}{20\textcolor{Blue}{\, \times \, 2}} \\ \\ &= \frac{5}{40} \div \frac{6}{40} \\ \\ &=\frac{5}{6}\end{align*}Cela s’explique bien en invoquant la règle d’or comme dans l’exemple suivant dans lequel on divise \(\frac{13}{18}\) par \(\frac{11}{24}\) : \begin{align*}\frac{13}{18} \div \frac{11}{24} &= \frac{\phantom{a} \frac{13}{18}\phantom{a}}{\frac{11}{24}} \\ \\ &= \frac{\phantom{a} \frac{13\textcolor{Blue}{\, \times \, 4}}{18\textcolor{Blue}{\, \times \, 4}}\phantom{a}}{\frac{11\textcolor{Blue}{\, \times \, 3}}{24\textcolor{Blue}{\, \times \, 3}}} \\ \\ &= \frac{\phantom{a}\frac{52}{72}\phantom{a}}{\frac{33}{72}} \\ \\ &=\frac{\phantom{a}\frac{52}{72}\textcolor{Blue}{\, \times \, 72}\phantom{a}}{\frac{33}{72}\textcolor{Blue}{\, \times \, 72}} \\ \\ &= \frac{52}{33}\end{align*}
En multipliant par l’inverse du diviseur
Bien sûr, lorsqu’on discute de la division de fractions, on ne peut s’abstenir de mentionner que cette division est équivalente à une multiplication du dividende par l’inverse du diviseur. D’un point de vue mathématique avancé, c’est une approche essentielle : la division est superflue. On est loin en première secondaire d’étudier les propriétés des corps en algèbre générale, mais la multiplication par l’inverse reste essentielle à maîtriser, ne serait-ce que pour certaines manipulations algébriques plus tard (ex: les opérations sur les fractions rationnelles en quatrième secondaire). \begin{align*}\frac{1}{10} \div \frac{4}{7} &= \frac{1}{10}\times \frac{7}{4} \\ \\ &= \frac{1 \times 7}{10 \times 4} \\ \\ &= \frac{7}{40}\end{align*}On peut bien sûr expliquer cette technique en ayant recours aux fractions équivalentes et à la règle d’or tel qu’illustré par cet autre exemple dans lequel on divise \(\frac{9}{25}\) par \(\frac{2}{3}\) : \begin{align*}\frac{9}{25} \div \frac{2}{3} &= \frac{\phantom{a} \frac{9}{25}\phantom{a}}{\frac{2}{3}} \\ \\ &= \frac{\phantom{a} \frac{9}{25}\textcolor{Blue}{\, \times \, \frac{3}{2}}\phantom{a}}{\frac{2}{3}\textcolor{Blue}{\, \times \, \frac{3}{2}}} \\ \\ &= \frac{\phantom{a} \frac{9}{25}\textcolor{Blue}{\, \times \, \frac{3}{2}}\phantom{a}}{1} \\ \\ &=\frac{9}{25}\textcolor{Blue}{\, \times \, \frac{3}{2}} \\ \\ &= \frac{9\times 3}{25 \times 2}\\ \\ &= \frac{27}{50}\end{align*}
En divisant les numérateurs ensemble et les dénominateurs ensemble
On termine enfin avec la technique utilisée par l’élève au début de ce billet. Est-elle valide ? Absolument ! Il est parfaitement possible de diviser les numérateurs ensemble et les dénominateurs ensemble, à l’instar de ce qu’on fait avec la multiplication.\begin{align*} \frac{75}{98} \div \frac{15}{49} &= \frac{75 \div 15}{98 \div 49} \\ \\ &= \frac{5}{2}\end{align*}Cela s’explique, encore une fois, vous l’aurez deviné, en invoquant la règle d’or. Considérons l’exemple suivant dans lequel on divise \(\frac{36}{55}\) par \(\frac{9}{11}\) : \begin{align*}\frac{36}{55} \div \frac{9}{11} &= \frac{\phantom{a}\frac{36}{55}\phantom{a}}{\frac{9}{11}} \\ \\ &= \frac{\phantom{a}\frac{36}{55}\color{Blue}{\, \div\, 9} \phantom{a}}{\frac{9}{11}\color{Blue}{\, \div \, 9}} \\ \\ &= \frac{\phantom{a}\frac{4}{55}\phantom{a}}{\frac{1}{11}} \\ \\ &=\frac{\phantom{a}\frac{4}{55}\color{Blue}{\, \times \, 11}\phantom{a}}{\frac{1}{11}\color{Blue}{\, \times \, 11}} \\ \\ &= \frac{\phantom{a}\frac{4\times 11}{55}\phantom{a}}{1} \\ \\ &= \frac{4\times 11}{55}\\ \\ &= \frac{4 \times 11 \color{Blue}{\, \div \, 11}}{55\color{Blue}{\, \div\, 11}}\\ \\ &= \frac{4}{55 \color{Blue}{\, \div \, 11}} \\ \\ &= \frac{4}{5}\end{align*}Le hic ? En général, cette stratégie n’est pas pratique. Elle l’est seulement lorsque le numérateur du dividende est un multiple du numérateur du diviseur et que le dénominateur du dividende est un multiple du dénominateur du diviseur. Si ce n’est pas le cas, on tourne en rond car on exprime la division de fractions… en une autre division de fractions équivalentes, tel qu’illustré dans cet exemple : \begin{align*}\frac{2}{3}\div \frac{7}{10} &=\frac{2\div 7}{3\div 10}\\ \\ &=\frac{2}{7}\div \frac{3}{10}\end{align*}Si on applique à nouveau la technique, on retrouve la division initiale. \begin{align*}\frac{2}{7}\div \frac{3}{10} &=\frac{2\div 3}{7\div 10}\\ \\ &=\frac{2}{3}\div \frac{7}{10}\end{align*}
[1] Conway, John H. et Richard Guy, The Book of Numbers, Corpenicus 1998