On connaît le périmètre d’un triangle et ses trois angles. On cherche les mesures des côtés.
Une de mes collègues vient me voir avec le corrigé de cet exercice et elle semble perplexe. On a le triangle suivant
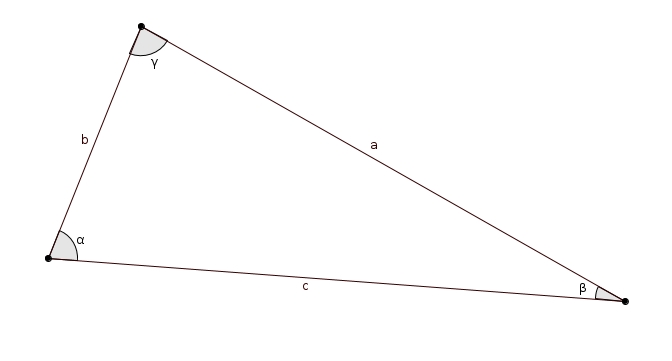 dans lequel on connaît périmètre, c’est-à-dire , et les trois angles , et . La première ligne du corrigé est ce qui, de prime abord, a tout l’air d’une erreur ! Le premier coup d’œil est cependant trompeur. On travaille si souvent avec les élèves la recherche d’un dénominateur commun lorsqu’on additionne ou soustrait des fractions qu’on voit mal les symboles d’égalité ! Ah, confusion !
dans lequel on connaît périmètre, c’est-à-dire , et les trois angles , et . La première ligne du corrigé est ce qui, de prime abord, a tout l’air d’une erreur ! Le premier coup d’œil est cependant trompeur. On travaille si souvent avec les élèves la recherche d’un dénominateur commun lorsqu’on additionne ou soustrait des fractions qu’on voit mal les symboles d’égalité ! Ah, confusion !
En effet, dans la loi des sinus, on a un rapport constant entre les sinus des angles et leur côté opposé. Ainsi, on a pour un certain (qui représente le diamètre du cercle circonscrit au triangle). C’est donc dire qu’on a et et On retrouve en effectuant la somme des trois équations précédentes et puis la mise en évidence de un côté de l’équation du départ Avec le rapport , il nous est maintenant possible de retrouver les mesures des côtés du triangle.
 dans lequel on connaît périmètre, c’est-à-dire
dans lequel on connaît périmètre, c’est-à-dire