On considère le diagramme suivant :
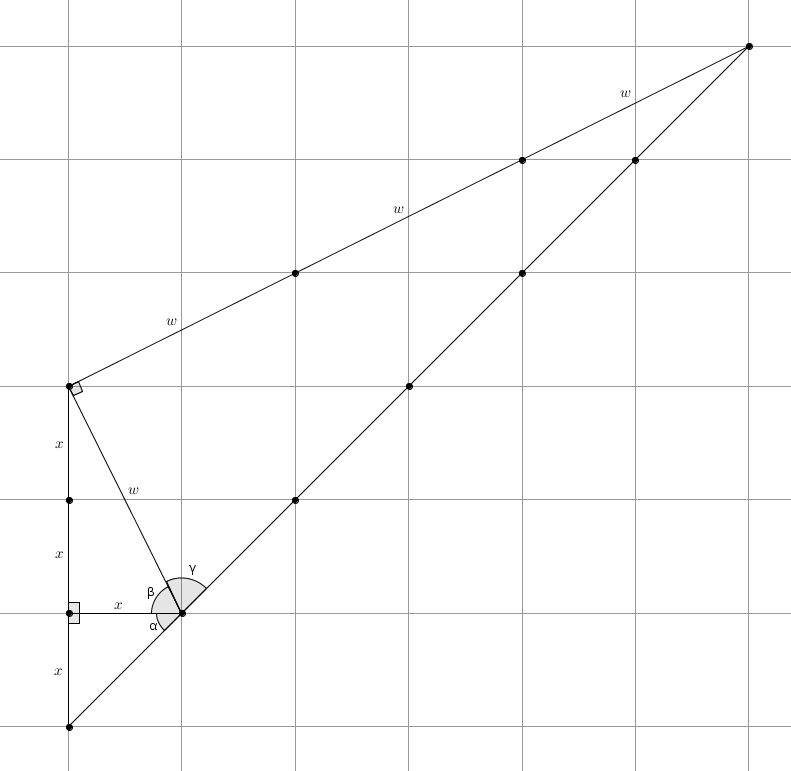
dans lequel \[\alpha+\beta+\gamma = 180^{\circ}\]et qui met en évidence la (surprenante) relation suivante : \[\arctan(1) + \arctan(2) + \arctan(3) = 180^{\circ}\]Le lecteur minutieux peut vérifier que le triangle possédant l’angle \(\gamma\) est bien rectangle. Avec Pythagore, on trouve dans le triangle possédant l’angle \(\beta\) \begin{align*} w^{2} &= x^{2} + \left(2x\right)^{2} \\ \\ &= 5x^{2}\end{align*}et donc que \[w = \sqrt{5}x\]Et comme la diagonale d’un carré de ce quadrillage a pour mesure \(\sqrt{2}x\), on vérifie la relation de Pythagore dans le grand triangle possédante l’angle \(\gamma\) \begin{align*}\left(3\sqrt{5}x\right)^{2} + \left(\sqrt{5}x\right)^{2} &= \left(5\sqrt{2}x\right)^{2} \\ \\ \left(9\cdot 5\right)x^{2} + 5x^{2} &= \left(25 \cdot 2\right)x^{2} \\ \\ 50x^{2}&=50x^{2}\end{align*}Il est donc rectangle. D’autres diagrammes ingénieux peuvent faire apparaître des relations surprenantes, je pense par exemple à celle-ci vue précédemment, ou encore à la suivante
\[\arctan\left(\frac{1}{2}\right) + \arctan\left(\frac{1}{3}\right) = 45^{\circ}\]
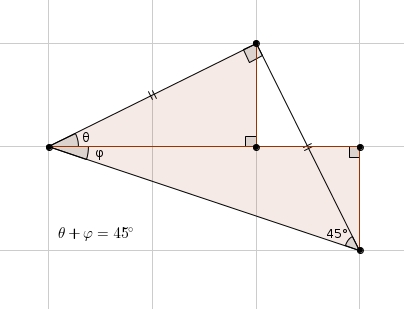
Référence : James Tanton (2012), Mathematics Galore !