$A\sin (x+\alpha )+B\cos (x+\beta )$

Bon, le titre n’est pas très original, et cette introduction ne l’est guère plus, mais nous allons nous intéresser aux expressions de cette forme $$A\sin (x+\alpha )+B\cos (x+\beta )$$Commençons d’abord avec le cas plus simple dans lequel $\alpha =0$ et $\beta =0$. Quiconque s’est déjà amusé à additionner des fonctions sinus ou cosinus (de même période) dans une calculatrice graphique a pu observer que le résultat est une fonction périodique qui ressemble à un sinusoïde. Par exemple, si je trace la fonction $$f(x)=3\sin (x)+4\cos (x)$$j’obtiens ce qui semble être une fonction périodique qui oscille entre $-5$ et $5$.

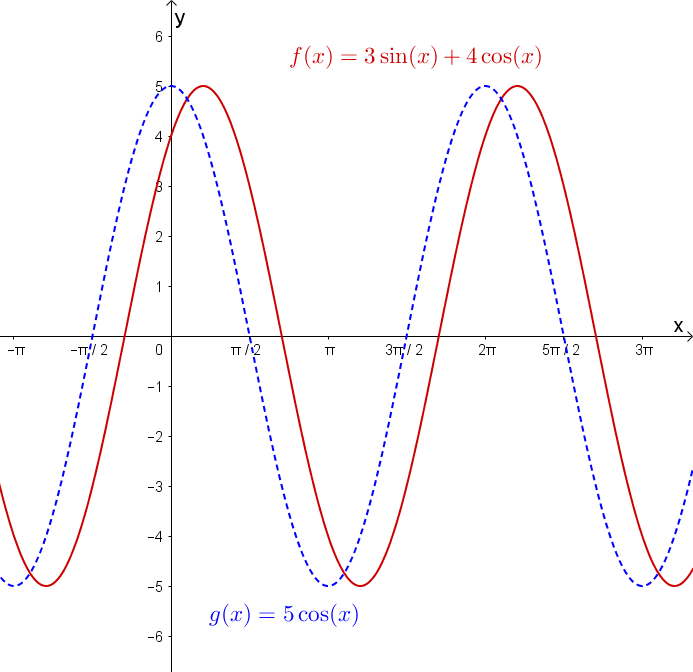
Si je trace en plus dans le même plan la fonction $$g(x)=5\cos (x)$$la ressemblance est frappante. Il semble s’agir de la même fonction, mais déphasée.

Les apparences ne sont pas trompeuses. La fonction $f$ est réellement un sinusoïde.

En effet, il est possible de trouver des valeurs $C$ et $\gamma$ telles que $$A\sin (x)+B\cos (x)=C\cos (x-\gamma )$$Avec la formule de différence d’angles du cosinus, on obtient $$\begin{array}{rl}C\cos (x-\gamma )& =C(\cos (x)\cos (\gamma )+\sin (x)\sin (\gamma ))\\ \\ & =C\sin (\gamma )\sin (x)+C\cos (\gamma )\cos (x)\end{array}$$En posant, $$A\sin (x)+B\cos (x)=C\sin (\gamma )\sin (x)+C\cos (\gamma )\cos (x)$$on observe que $A=C\sin (\gamma )$ et $B=C\cos (\gamma )$. Comment déterminer les valeurs de $C$ et $\gamma$ pour une somme donnée ? On utilise deux relations trigonométriques bien connues. Pour $C$, on a $$\begin{array}{rl}{A}^2+B^2& ={(C\sin (\gamma ))}^2+{(C\cos (\gamma ))}^2\\ \\ & =C^2{\sin }^2(\gamma )+C^2{\cos }^2(\gamma )\\ \\ & =C^2({\sin }^2(\gamma )+{\cos }^2(\gamma ))\\ \\ & =C^2\end{array}$$car $${\sin }^2(\gamma )+{\cos }^2(\gamma )=1$$On obtient donc$$C=\pm \sqrt{A^2+B^2}$$Pour $\gamma$, on a $$\begin{array}{rl}\frac{A}{B}& =\frac{C\sin (\gamma )}{C\cos (\gamma )}\\ \\ & =\frac{\cancel{C}\sin (\gamma )}{\cancel{C}\cos (\gamma )}\\ \\ & =\frac{\sin (\gamma )}{\cos (\gamma )}\\ \\ & =\tan (\gamma )\end{array}$$On obtient donc$$\gamma =\arctan \left(\frac{A}{B}\right)$$Il est possible de toujours choisir la racine positive pour $C$ en ajustant la valeur de $\gamma$. Si $B\ge 0$, $\gamma =\arctan \left(\frac{A}{B}\right)$ alors que si $B<0$, $\gamma =\arctan \left(\frac{A}{B}\right)+\pi$. Si on préfère s’en tenir aux valeurs de l’arctangente sans ajustement, on peut aussi choisir la racine négative $C=-\sqrt{A^2+B^2}$ lorsque $B<0$ et positive $C=\sqrt{A^2+B^2}$ lorsque $B\ge 0$.

Entre autres choses, cela nous permet de résoudre des équations de cette forme ou de trouver des maximums ou des minimums plus aisément.

Résoudre $$12\sin (x)+5\cos (x)=0$$sur l’intervalle $[0,2\pi ]$

On pose $$\begin{array}{rl}C& =\sqrt{{12}^2+5^2}\\ \\ & =\sqrt{144+25}\\ \\ & =\sqrt{169}\\ \\ & =13\end{array}$$ainsi que $$\begin{array}{rl}\gamma & =\arctan \left(\frac{12}{5}\right)\\ \\ & =\arctan (2,4)\\ \\ & \approx 1,176\end{array}$$On peut donc résoudre $$13\cos (x-\arctan (2,4))=0$$On divise par $13$ de chaque côté $$\cos (x-\arctan (2,4))=0$$On obtient $$x-\arctan (2,4)=\frac{\pi }{2}$$ ou $$x-\arctan (2,4)=\frac{3\pi }{2}$$ce qui fait $$\begin{array}{rl}x& =\frac{\pi }{2}+\arctan (2,4)\\ \\ & \approx 2,747\end{array}$$ ou $$\begin{array}{rl}x& =\frac{3\pi }{2}+\arctan (2,4)\\ \\ & \approx 5,888\end{array}$$

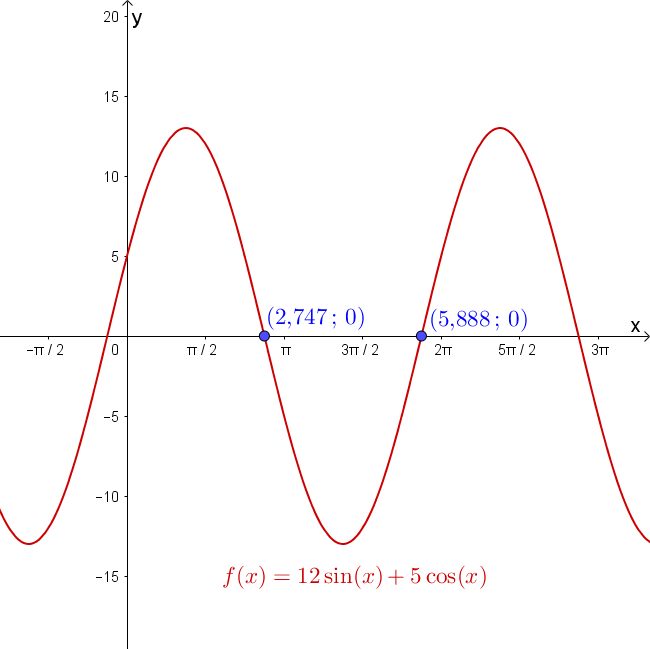
Quel est le maximum de la fonction $$f(x)=8\sin (x)+15\cos (x)$$sur l’intervalle $[0,2\pi ]$ et pour quelle valeur de $x$ a-t-on ce maximum ?

On pose $$\begin{array}{rl}C& =\sqrt{8^2+{15}^2}\\ \\ & =\sqrt{64+225}\\ \\ & =\sqrt{189}\\ \\ & =17\end{array}$$ainsi que $$\begin{array}{rl}\gamma & =\arctan \left(\frac{8}{15}\right)\\ \\ & \approx 0,490\end{array}$$

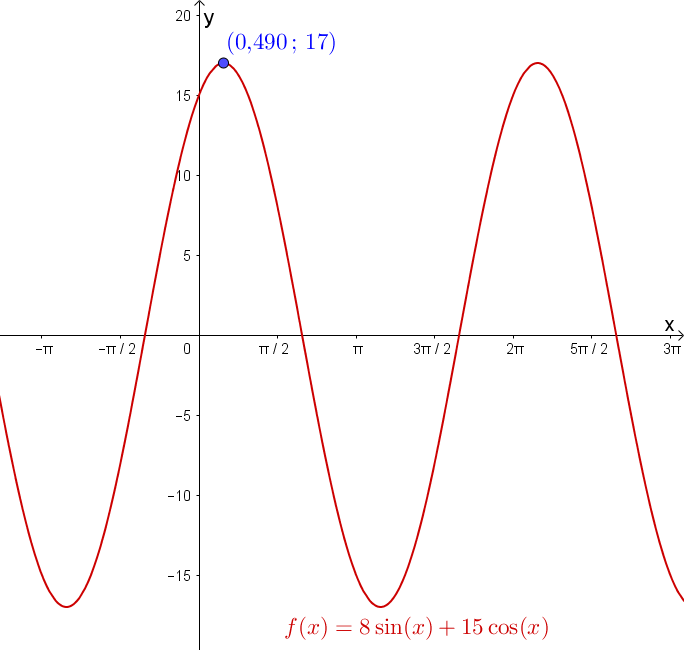
Le maximum de la fonction $$g(x)=17\cos (x-\arctan \left(\frac{8}{15}\right))$$ est $17$ et celui-ci est obtenu lorsque $x=\arctan \left(\frac{8}{15}\right)\approx 0,490$.

Si $\alpha \ne 0$ et/ou $\beta \ne 0$

Qu’arrive-t-il si $\alpha \ne 0$ ou $\beta \ne 0$ ? La somme est-elle encore un sinusoïde si une des deux fonctions (ou les deux) a d’abord subi un déphasage ? La réponse est oui. Il suffit d’appliquer les formules d’addition d’angles et de regrouper. $$\begin{array}{rl}A\sin (x+\alpha )+B\cos (x+\beta )& =A(\sin (x)\cos (\alpha )+\sin (\alpha )\cos (x))+B(\cos (x)\cos (\beta )-\sin (x)\sin (\beta ))\\ \\ & =A\cos (\alpha )\sin (x)+A\sin (\alpha )\cos (x)+B\cos (\beta )\cos (x)-B\sin (\beta )\sin (x)\\ \\ & =(A\cos (\alpha )-B\sin (\beta ))\sin (x)+(A\sin (\alpha )+B\cos (\beta ))\cos (x)\end{array}$$On retrouver une expression de la forme $$A_1\sin (x)+B_1\cos (x)$$dans laquelle $A_1=A\cos (\alpha )-B\sin (\beta )$ et $B_1=A\sin (\alpha )+B\cos (\beta )$.

Un exemple numérique

Considérons l’expression $$5\sin (x+\frac{5\pi }{6})+3\cos (x+\frac{2\pi }{3})$$On applique les formules d’addition d’angles $$\begin{array}{rl}5\sin (x+\frac{5\pi }{6})+3\cos (x+\frac{2\pi }{3})& =5(\sin (x)\cos \left(\frac{5\pi }{6}\right)+\sin \left(\frac{5\pi }{6}\right)\cos (x))+3(\cos (x)\cos \left(\frac{2\pi }{3}\right)-\sin (x)\sin \left(\frac{2\pi }{3}\right))\\ \\ & =5\cos \left(\frac{5\pi }{6}\right)\sin (x)-3\sin \left(\frac{2\pi }{3}\right)\sin (x)+5\sin \left(\frac{5\pi }{6}\right)\cos (x)+3\cos \left(\frac{2\pi }{3}\right)\cos (x)\\ \\ & =(5\cos \left(\frac{5\pi }{6}\right)-3\sin \left(\frac{2\pi }{3}\right))\sin (x)+(5\sin \left(\frac{5\pi }{6}\right)+3\cos \left(\frac{2\pi }{3}\right))\cos (x)\\ \\ & =(5(-\frac{\sqrt{3}}{2})-3(-\frac{\sqrt{3}}{2}))\sin (x)+(5\left(\frac{1}{2}\right)+3(-\frac{1}{2}))\cos (x)\\ \\ & =\left(\frac{-8\sqrt{3}}{2}\right)\sin (x)+\cos (x)\\ \\ & =-4\sqrt{3}\sin (x)+\cos (x)\end{array}$$

On a une expression de la forme $$A\sin (x)+B\cos (x)$$ avec $A=-4\sqrt{3}$ et $B=1$. On trouve $$\begin{array}{rl}C& =\pm \sqrt{{(-4\sqrt{3})}^2+1^2}\\ \\ & =\sqrt{48+1}\\ \\ & =\sqrt{49}\\ \\ & =7\end{array}$$D’autre part, on trouve $$\begin{array}{rl}\gamma & =\arctan \left(\frac{-4\sqrt{3}}{1}\right)\\ \\ & \approx -1,427449\end{array}$$Ainsi, on peut vérifier avec la calculatrice graphique que $$\begin{array}{rl}5\sin (x+\frac{5\pi }{6})+3\cos (x+\frac{2\pi }{3})& =7\cos (x-\arctan (-4\sqrt{3}))\\ \\ & \approx 7\cos (x+1,427449)\end{array}$$