Voici une solution simple et élégante au problème difficile suivant : découpez un carré en triangles acutangles. Si vous n’aviez jamais rencontré ce problème, je vous conseille de chercher un peu par vous-même. C’est plus difficile que ça en a l’air ! Commencez peut-être par chercher une solution à \(14\) triangles ou plus.
La solution suivante vient de David Eppstein et elle ne comporte que \(8\) triangles (pourrait-on trouver une solution comportant moins de \(8\) triangles ?)
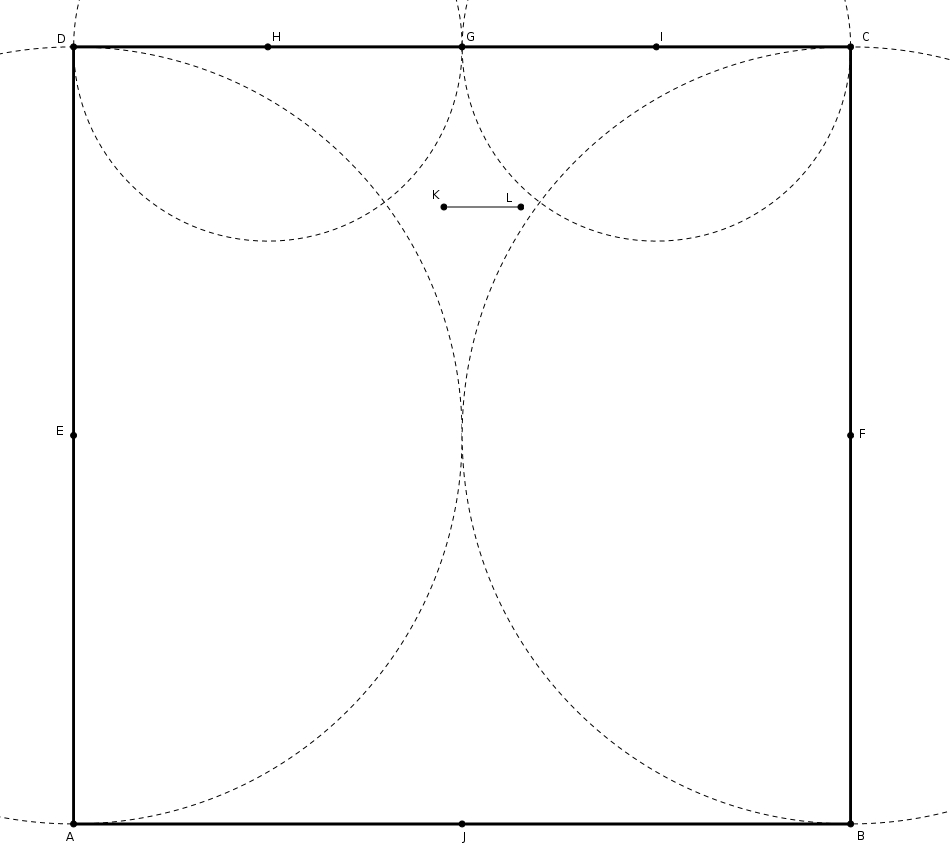
Considérons le carré \(ABCD\). Identifiez les points milieux \(E\) de \(\overline{AD}\), \(G\) de \(\overline{CD}\), \(F\) de \(\overline{BC}\) et \(J\) de \(\overline{AB}\). Identifiez aussi les points milieux \(H\) de \(\overline{DG}\) et \(I\) de \(\overline{CG}\). Tracez ensuite les cercles de centre \(E\) et de rayon \(AE\), de centre \(F\) et de rayon \(BF\), de centre \(H\) et de rayon \(DH\) et de centre \(I\) et de rayon \(CI\). Tel qu’illustré ci-dessous, considérez un point \(K\) dans la zone extérieure aux quatre cercles. Considérez aussi un deuxième point \(L\) dans cette même zone, de l’autre côté de \(\overline{GJ}\) que \(K\), et de telle sorte que le segment \(KL\) soit parallèle à \(\overline{DC}\).
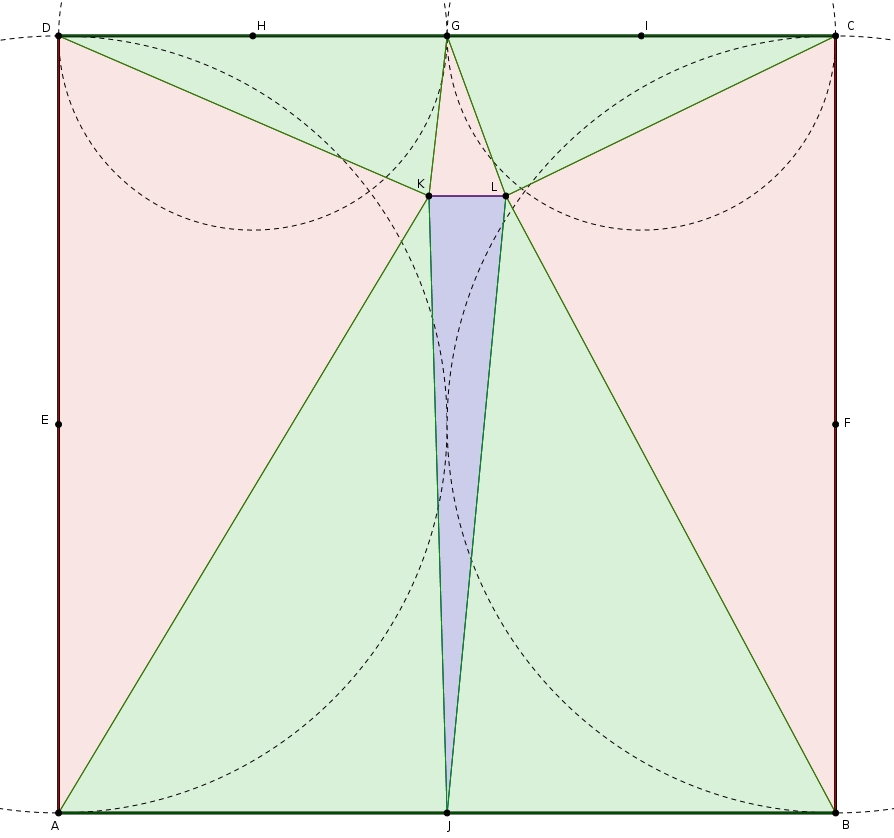
Puisque le point \(K\) est à l’extérieur des cercles, cela nous assure que les angles \(DKG\) ou \(DKA\) sont aigus. La même chose s’applique au point \(L\). La solution est donc composée des triangles suivants, qui sont tous définitivement acutangles !
