Exercice de géométrie analytique

Le théorème de Von Aubel

Dans un quadrilatère quelconque, on construit quatre carrés extérieurs aux quatre côtés du quadrilatère.  Le théorème de Von Aubel nous dit que les segments qui joignent les centres des carrés opposés sont de même longueur et se croisent perpendiculairement.

Dans la figure suivante, quatre carrés dont les centres sont $P_1$, $P_2$, $P_3$ et $P_4$ sont construits sur les côtés du quadrilatère $ABCD$.

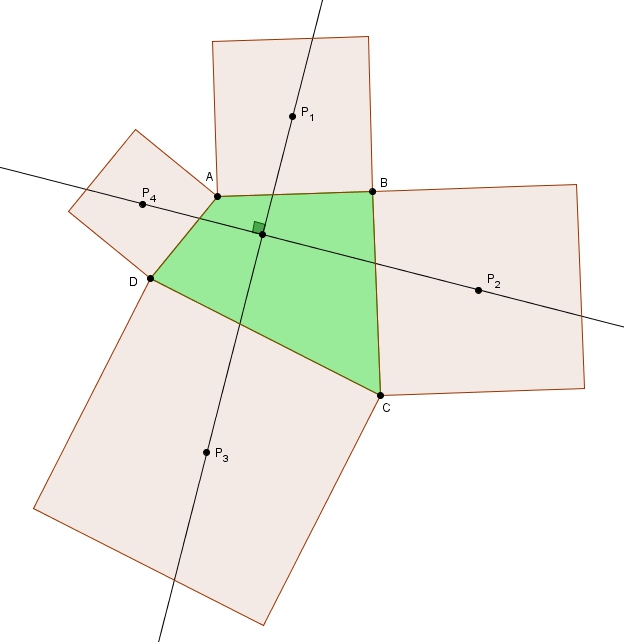
Selon le théorème, on a donc $$m\overline{P_1{P}_3}=m\overline{P_2{P}_4}$$et $$P_1{P}_3\perp P_2{P}_4$$Je vous conseille d’ouvrir la figure dynamique ici.  Notez que le quadrilatère peut être concave et même croisé.

Le théorème de Von Aubel est souvent abordé comme un exercice dans le plan complexe.  Il peut aussi être vu beaucoup plus tôt avec pour seuls outils quelques notions de géométrie analytique.

Considérons dans un premier temps le carré $RSTU$ suivant

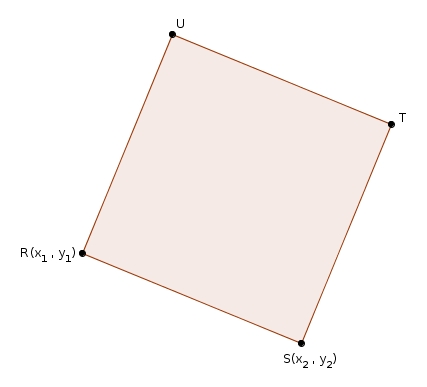dans lequel les coordonnées de $R$ et $S$ sont respectivement $(x_1,y_1)$ et $(x_2,y_2)$.

On exprime d’abord les coordonnées de $T$ en fonction des coordonnées de $R$ et $S$.

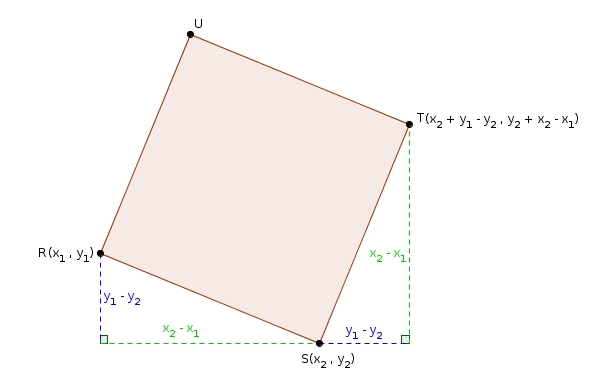
Les coordonnées de $T$ sont donc $$T(x_2+y_1-y_2,y_2+x_2-x_1)$$Par la suite, on détermine les coordonnées du point milieu de la diagonale (le point $M$ sur l’illustration).

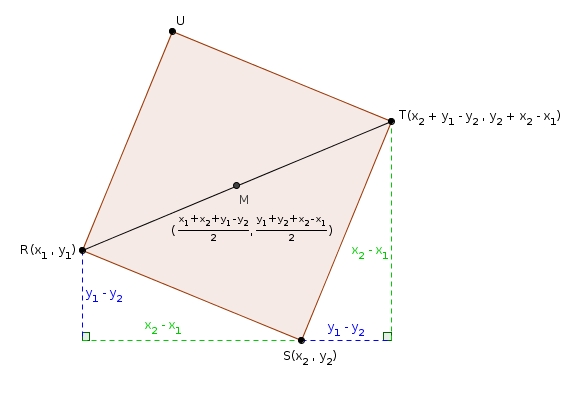
Les coordonnées de $M$ sont $$M(\frac{x_1+x_2+y_1-y_2}{2},\frac{y_1+y_2+x_2-x_1}{2})$$Considérons le quadrilatère $ABCD$ suivant et construisons les carrés de centre $P_1$, $P_2$, $P_3$ et $P_4$ sur les côtés extérieurs du quadrilatère.

En posant les coordonnées $$A(a,b),B(c,d),C(e,f),D(g,h)$$on peut exprimer les coordonnées de $P_1$, $P_2$, $P_3$ et $P_4$ : $$\begin{array}{rl}& P_1(\frac{a+b+c-d}{2},\frac{b+c+d-a}{2})\\ \\ & P_2(\frac{c+d+e-f}{2},\frac{d+e+f-c}{2})\\ \\ & P_3(\frac{e+f+g-h}{2},\frac{f+g+h-e}{2})\\ \\ & P_4(\frac{g+h+a-b}{2},\frac{h+a+b-g}{2})\end{array}$$Il nous est possible de calculer la pente de $P_1{P}_3$ :$$\text{pente}(P_1{P}_3)=\frac{\frac{b+c+d-a}{2}-\frac{f+g+h-e}{2}}{\frac{a+b+c-d}{2}-\frac{e+f+g-h}{2}}$$ce qui fait en multipliant le numérateur et le dénominateur par $2$ $$\text{pente}(P_1{P}_3)=\frac{b+c+d-a-f-g-h+e}{a+b+c-d-e-f-g+h}$$ou $$\text{pente}(P_1{P}_3)=\frac{b+c+d+e-(a+f+g+h)}{a+b+c+h-(d+e+f+g)}$$On calcule par la suite la pente de $P_2{P}_4$ $$\text{pente}(P_2{P}_4)=\frac{\frac{d+e+f-c}{2}-\frac{h+a+b-g}{2}}{\frac{c+d+e-f}{2}-\frac{g+h+a-b}{2}}$$ce qui fait encore une fois $$\text{pente}(P_2{P}_4)=\frac{d+e+f-c-h-a-b+g}{c+d+e-f-g-h-a+b}$$et donc $$\text{pente}(P_2{P}_4)=\frac{d+e+f+g-(a+b+c+h)}{b+c+d+e-(a+f+g+h)}$$Cette fois-ci on met en évidence un facteur $(-1)$ au numérateur $$\text{pente}(P_2{P}_4)=\frac{(-1)(a+b+c+h-(d+e+f+g))}{b+c+d+e-(a+f+g+h)}$$ce qui donne en réécrivant $$\text{pente}(P_2{P}_4)=(-1)\cdot \frac{a+b+c+h-(d+e+f+g)}{b+c+d+e-(a+f+g+h)}$$c’est à dire l’opposé de l’inverse de ce que l’on avait obtenu pour la pente de $P_1{P}_3$ $$\text{pente}(P_1{P}_3)=\frac{b+c+d+e-(a+f+g+h)}{a+b+c+h-(d+e+f+g)}$$Et des droites dont les pentes sont l’opposé de l’inverse l’une de l’autre sont perpendiculaires !

Pour ce qui est des mesures des segments.  Il nous est possible d’exprimer la mesure du segment $P_1{P}_3$ $$m\overline{P_1{P}_3}=\sqrt{{(\frac{a+b+c-d}{2}-\frac{e+f+g-h}{2})}^2+{(\frac{b+c+d-a}{2}-\frac{f+g+h-e}{2})}^2}$$ce qui fait $$m\overline{P_1{P}_3}=\sqrt{{\left(\frac{a+b+c+h-(d+e+f+g)}{2}\right)}^2+{\left(\frac{b+c+d+e-(a+f+g+h)}{2}\right)}^2}$$Il serait possible de simplifier davantage l’expression précédente mais cela ne nous sera pas nécessaire.  De la même manière, on exprime ensuite la mesure du segment $P_2{P}_4$ $$m\overline{P_2{P}_4}=\sqrt{{(\frac{c+d+e-f}{2}-\frac{g+h+a-b}{2})}^2+{(\frac{d+e+f-c}{2}-\frac{h+a+b-g}{2})}^2}$$ce qui fait $$m\overline{P_2{P}_4}=\sqrt{{\left(\frac{b+c+d+e-(a+f+g+h)}{2}\right)}^2+{\left(\frac{d+e+f+g-(a+b+c+h)}{2}\right)}^2}$$Et comme on l’avait fait précédemment, on met en évidence un facteur $(-1)$ au numérateur de la deuxième fraction $$m\overline{P_2{P}_4}=\sqrt{{\left(\frac{b+c+d+e-(a+f+g+h)}{2}\right)}^2+{((-1)\cdot \frac{a+b+c+h-(d+e+f+g)}{2})}^2}$$Le carré d’un produit étant égal au produit des carrés on obtient $$m\overline{P_2{P}_4}=\sqrt{{\left(\frac{b+c+d+e-(a+f+g+h)}{2}\right)}^2+(-1{)}^2{\left(\frac{a+b+c+h-(d+e+f+g)}{2}\right)}^2}$$et enfin comme $(-1{)}^2$ est tout simplement égal à $1$, on a $$m\overline{P_2{P}_4}=\sqrt{{\left(\frac{b+c+d+e-(a+f+g+h)}{2}\right)}^2+{\left(\frac{a+b+c+h-(d+e+f+g)}{2}\right)}^2}$$c’est-à-dire $$m\overline{P_1{P}_3}=m\overline{P_2{P}_4}$$Voilà !