Icosaèdre régulier

On avait déjà vu sur ce blogue que la valeur exacte du cosinus de \(36^{\circ}\) est \[\cos(36^{\circ}) = \frac{1+\sqrt{5}}{4}\]

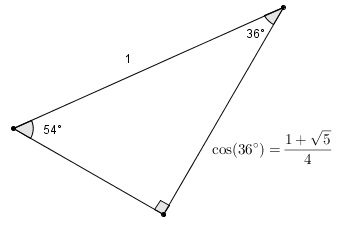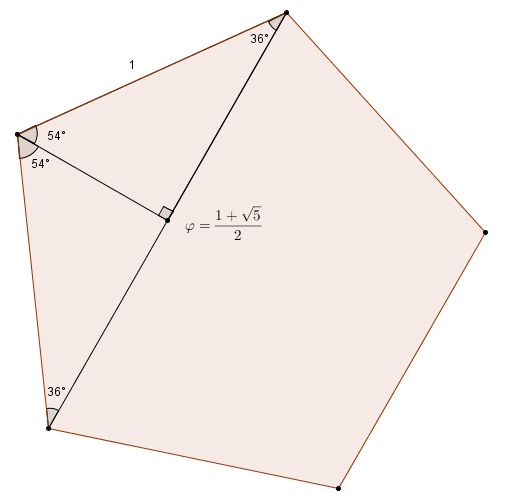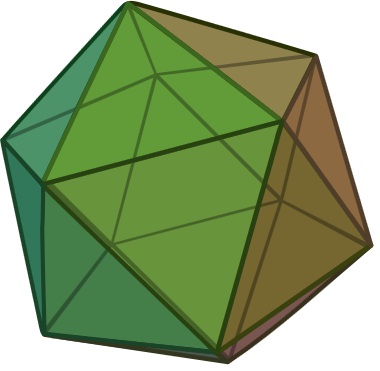
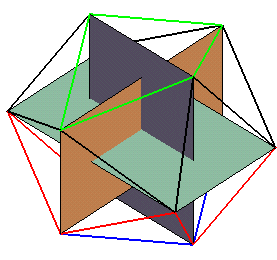
L’angle intérieur d’un pentagone régulier étant de \(108^{\circ}\), cette valeur nous permet de trouver le rapport entre la mesure d’un côté d’un pentagone régulier et la mesure de sa diagonale,ce rapport étant égal au double du cosinus de \(36^{\circ}\) : le nombre d’or (noté \(\varphi\)) ! L’icosaèdre régulier est un des cinq polyèdres réguliers. Ses \(20\) faces sont des triangles équilatéraux isométriques et à chaque sommet se rejoignent \(5\) faces.

Ainsi, en considérant les cinq faces triangulaires isométriques partant d’un sommet, il est possible d’identifier un ensemble d’arêtes qui sont coplanaires et qui forment un pentagone régulier.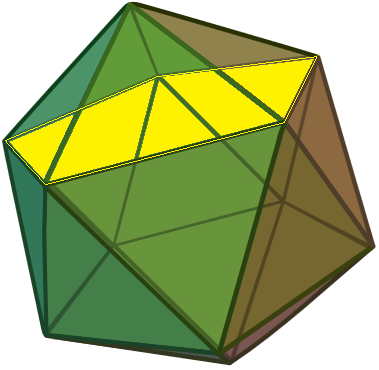

Cette remarque, bien qu’elle soit incomplète, nous permet néanmoins d’apprécier la jolie construction suivante,

un assemblage de trois rectangles dans les proportions « divines » (c’est-à-dire du nombre d’or). Les plus petits côtés des rectangles correspondent à des arêtes alors que les plus grands, des diagonales de pentagones. Cela nous permet aussi de visualiser les coordonnées cartésiennes des sommets d’un icosaèdre régulier (dont les arêtes, par soucis de simplicité et d’élégance, mesurent \(2\) unités) \[\left(\pm\varphi,\, \pm 1, \, 0\right)\, , \quad \left(\pm1,\, 0,\, \pm\varphi\right)\, , \quad \left(0,\, \pm\varphi,\, \pm 1\right)\]Bien sûr, cette longue introduction à ce court billet n’avait en réalité d’autre but que de vous présenter l’icosaèdre de votre humble serviteur

Fait en quelques minutes avant l’affectation des postes ! Disons seulement que ça manque un peu de couleurs…

Référence : H.S.M. Coxeter (1989), Introduction to Geometry 2^nd Edition

Wikipedia et Mathcurve pour certaines images.