La preuve par induction est souvent courte et commodément efficace, même économique, mais elle remplace parfois d’autres méthodes généralement plus riches et plus belles. On arrive parfois à se demander comment aurait-on pu « deviner » l’hypothèse d’induction (pensez à certaines preuves en analyse ou en mathématiques discrètes). Cela laisse à l’occasion un goût amer dans la bouche.
Voici donc une jolie preuve par induction, bien courte, d’un résultat qui semble de prime abord intangible et imperméable à nos lignes d’attaque habituelles.
On trace \(n\) droites dans le plan. Les régions ainsi formées par les \(n\) droites peuvent toujours être coloriées avec deux couleurs, de manière à ce qu’aucune région ait la même couleur que sa ou ses régions voisines, c’est-à-dire les régions qui partagent avec elle un segment de droite comme frontière.
Notre hypothèse d’induction est donc qu’on peut colorier les régions d’un plan contenant \(n\) droites. On considère un plan avec \(n+1\) droites. On enlève une droite parmi les \(n+1\) : il en reste seulement \(n\) et par l’hypothèse, il est possible de colorier les régions du plan formées par les \(n\) droites.On réintroduit la \((n+1)\)ième droite.
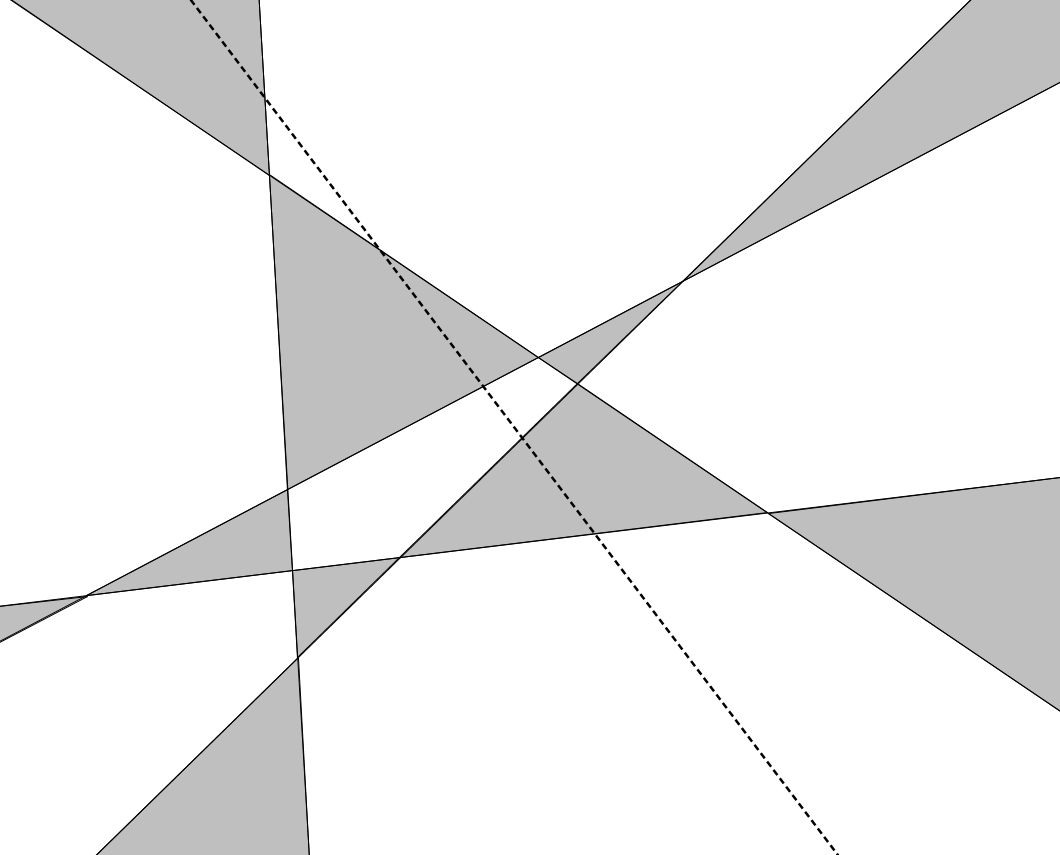Cette droite sépare le plan en deux demi-plans. On choisit un de ces deux demi-plans et on change systématiquement les couleurs dans chacune des régions de ce demi-plan : les régions noires deviennent blanches et les régions blanches deviennent noires. On laisse l’autre demi-plan (de l’autre côté de la droite) intact. Le plan est maintenant adéquatement colorié !
En effet,- si deux régions du plan séparé par les \(n+1\) droites ont une frontière composée d’un segment appartenant à une des premières \(n\) droites, alors ces régions avaient déjà des couleurs différentes avant l’introduction de la \((n+1)\)ième droite. En introduisant la \((n+1)\)ième droite, on laisse ces couleurs déjà différentes telles quelles ou on les changes toutes les deux.
- si deux régions ont une frontière composée d’un segment appartenant à la \((n+1)\)ième droite, alors avant l’introduction de la \((n+1)\)ième droite, elles faisaient partie de la même région et donc étaient coloriées de la même couleur. En introduisant la \((n+1)\)ième droite, on change les couleurs d’une des deux régions, d’un côté de la droite, mais pas de l’autre. Ces régions nouvellement voisines ont donc maintenant des couleurs différentes.
Référence : Akiva Moiseevich Yaglom et Isaak Moiseevich Yaglom (1967), Challenging Mathematical Problems with Elementary Solutions Vol. II