Inégalité MA-MG pour deux nombres

On avait déjà vu ici cette image :

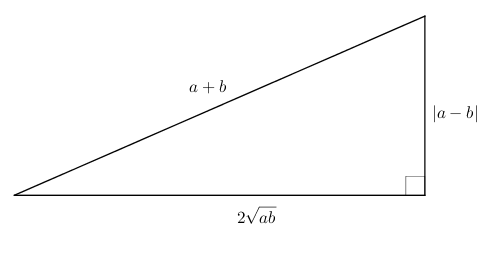
Le triangle est rectangle car la relation de Pythagore est vérifiée : $$\begin{array}{rl}{\left(2\sqrt{ab}\right)}^2+{\left(|a-b|\right)}^2& ={\left(2\sqrt{ab}\right)}^2+{(a-b)}^2\\ \\ & =4ab+a^2-2ab+b^2\\ \\ & =a^2+2ab+b^2\\ \\ & ={(a+b)}^2\end{array}$$

Les mesures des cathètes étant strictement inférieures à celle de l’hypoténuse, on trouve $$a+b>2\sqrt{ab}$$ou, en divisant par $2$, $$\frac{a+b}{2}>\sqrt{ab}$$On peut vérifier qu’on a l’égalité $$\frac{a+b}{2}=\sqrt{ab}$$si $a=b$.

Voici une autre « preuve sans mots ».

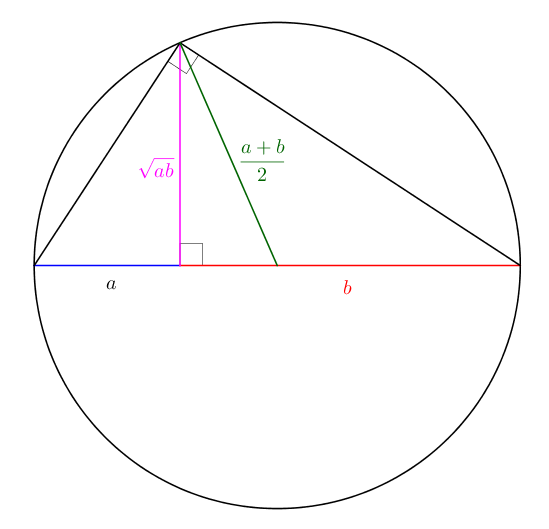
Le cercle de diamètre $a+b$ a un rayon $\frac{a+b}{2}$. Le grand triangle inscrit est sous-tendu par un diamètre, il est donc rectangle. La hauteur $h$ relative à l’hypoténuse est $$\frac{h}{a}=\frac{b}{h}$$ce qui fait $$h^2=ab$$ou $$h=\sqrt{ab}$$

La mesure de l’hypoténuse d’un triangle rectangle étant strictement supérieure à celles de ses cathètes, on a bien $$\frac{a+b}{2}>\sqrt{ab}$$Encore, une fois, on peut vérifier qu’on a l’égalité $$\frac{a+b}{2}=\sqrt{ab}$$si $a=b$.