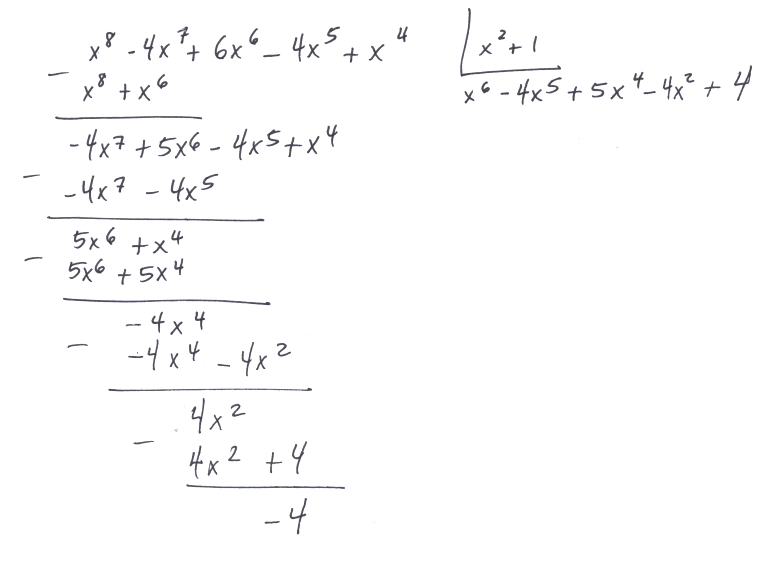Intégrale

Exercice : on doit évaluer l’intégrale définie suivante$${\int }_0^1\frac{x^4{(1-x)}^4}{1+x^2}\text{d}x$$On effectue la longue division afin d’obtenir, on l’espère, des termes plus faciles à intégrer.  Cette dernière me donne

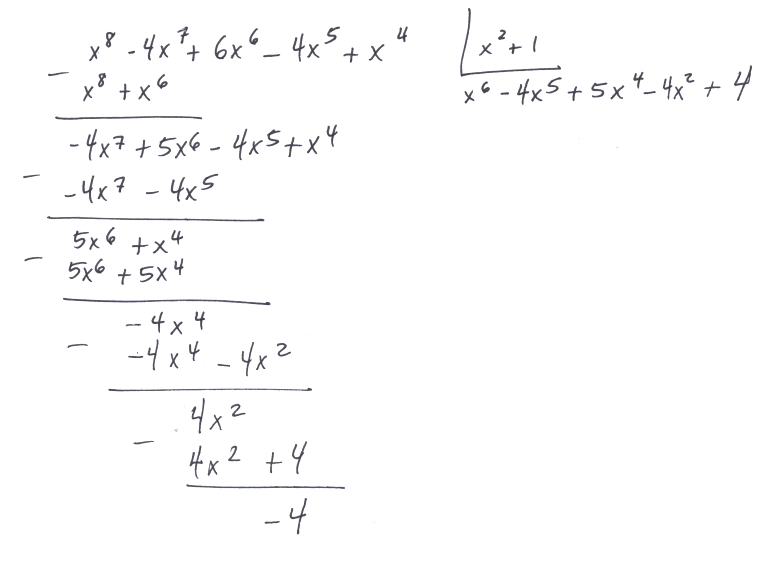
La longue division polynomiale avec crochet

et on a donc$${\int }_0^1\frac{x^4{(1-x)}^4}{1+x^2}\text{d}x={\int }_0^1{x}^6-4x^5+5x^4-4x^2+4-4\left(\frac{1}{1+x^2}\right)\text{d}x$$En évaluant cette intégrale terme à terme, on obtient$$\begin{array}{rl}{\int }_0^1\frac{x^4{(1-x)}^4}{1+x^2}\text{d}x& ={\int }_0^1{x}^6-4x^5+5x^4-4x^2+4-4\left(\frac{1}{1+x^2}\right)\text{d}x\\ \\ & ={[\frac{x^7}{7}-\frac{4x^6}{6}+\frac{5x^5}{6}-\frac{4x^3}{3}+4x-4\arctan \left(x\right)]}_0^1\\ \\ & ={[\frac{x^7}{7}-\frac{2x^6}{3}+x^5-\frac{4x^3}{3}+4x-4\arctan \left(x\right)]}_0^1\end{array}$$Comme on a en plus $$\arctan \left(0\right)=0$$et$$\arctan \left(1\right)=\frac{\pi }{4}$$on obtient $$\begin{array}{rl}{\int }_0^1\frac{x^4{(1-x)}^4}{1+x^2}\text{d}x& ={[\frac{x^7}{7}-\frac{2x^6}{3}+x^5-\frac{4x^3}{3}+4x-4\arctan \left(x\right)]}_0^1\\ \\ & =\frac{1^7}{7}-\frac{2\cdot 1^6}{3}+1^5-\frac{4\cdot 1^3}{3}+4\cdot 1–4\arctan \left(1\right)\\ \\ & =\frac{1}{7}-\frac{2}{3}+1-\frac{4}{3}+4-4\frac{\pi }{4}\\ \\ & =\frac{22}{7}-\pi \end{array}$$un résultat particulièrement attrayant.

Comme l’intégrande est positif (il s’agit d’un quotient dans lequel le numérateur et le dénominateur sont tous deux positifs), et qu’en inspectant les bornes, $0<1$, l’intégrale sera positive. Cela nous montre de manière élégante, mais peu économique, que $\frac{22}{7}$ est plus grand que $\pi$.

Référence : Julian Havil (2009), Gamma : Exploring Euler’s Constant