Nous avons déjà vu sur ce blogue une preuve de la formule de la distance d’un point à une droite dans le plan cartésien lorsque l’équation de la droite est donnée sous la forme générale\[Ax + By + C = 0\]Mon collègue Dominik m’a partagé cette preuve dans laquelle l’équation de la droite est sous la forme fonctionnelle \[y = ax + b\]La preuve est courte, implique peu de calculs, et est essentiellement géométrique. Elle est plus simple et plus élégante. On considère donc un point \(P\) de coordonnées \((x_{0},\, y_{0})\) et une droite \(D_{1}\) dans le plan.
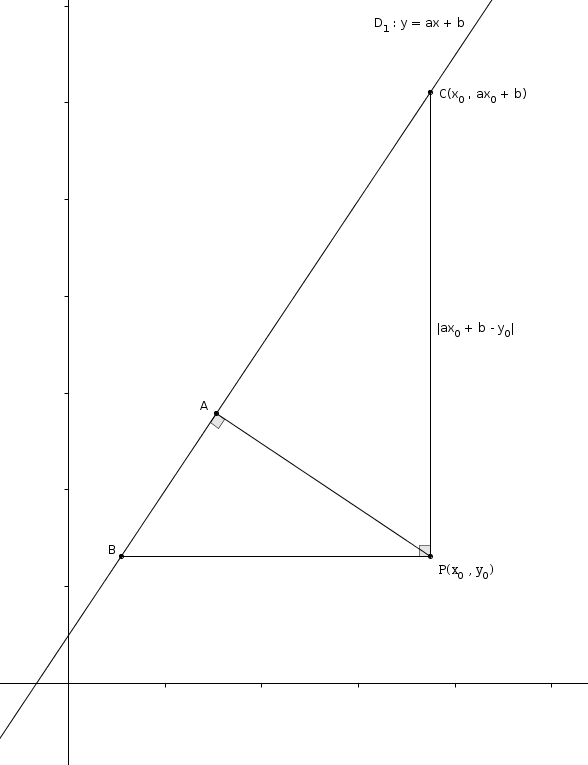
La distance de \(P\) à \(D_{1}\) correspond à la mesure du segment \(AP\) dans la figure. On place ensuite \(B\) et \(C\) sur \(D_{1}\) de telle sorte que \(B\) ait la même abscisse que \(P\) et \(C\) ait la même ordonnée que \(P\). En d’autres mots, on forme un triangle \(BPC\) rectangle en \(P\) et dont les cathètes \(BP\) et \(CP\) sont parallèles aux axes (respectivement des abscisses et des ordonnées). Le segment \(AP\) est une hauteur issue de l’angle droit (ou relative à l’hypoténuse) du triangle rectangle \(BPC\). Une telle hauteur forme des triangles semblables. En particulier, les triangles \(BPC\) et \(PAC\) sont semblables. Comme \(C\) est sur \(D_{1}\) et qu’il possède la même abscisse que \(P\), on trouve que ses coordonnées sont \[C\left(x_{0},\, ax_{0}+b\right)\]et on trouve aussi que la mesure du segment vertical \(CP\) est \[\vert ax_{0} + b-y_{0}\vert \]
On place ensuite \(D\) sur \(BP\) à une unité de \(B\). On place \(E\) sur \(D_{1}\) de manière à former un autre triangle \(BDE\) rectangle en \(D\). Comme dans la forme fonctionnelle le coefficient \(a\) correspond à la pente de la droite, on trouve immédiatement que \(DE\) a pour mesure \(\vert a\vert\). Il s’en suit aussi qu’avec Pythagore,\[m\overline{EB}=\sqrt{1+a^{2}}\](la valeur absolue étant maintenant superflue avec le carré)
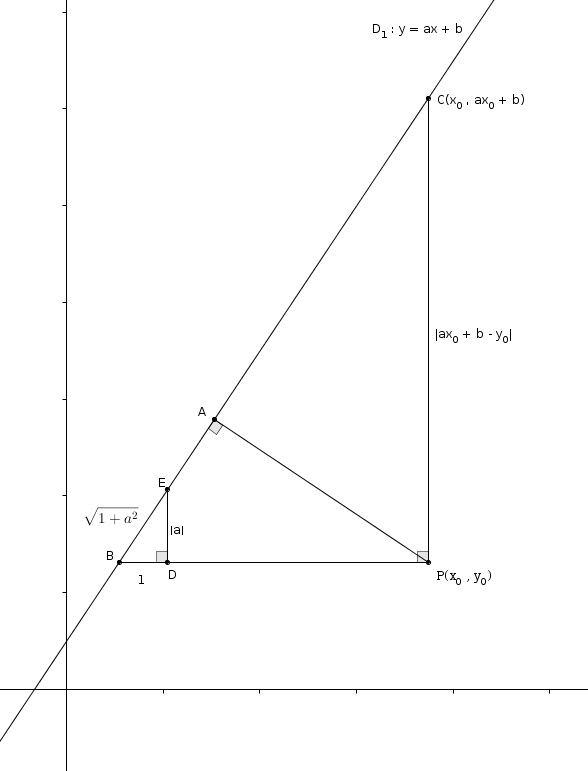
Par le cas de similitude AA les triangles \(BDE\) et \(BPC\) sont semblables. Par transitivité, on trouve aussi que les triangles \(BDE\) et \(PAC\) sont semblables. Avec la proportion \[\frac{m\overline{AP}}{m\overline{DB}} = \frac{m\overline{CP}}{m\overline{EB}}\]on trouve en remplaçant \[\frac{m\overline{AP}}{1} = \frac{\vert ax_{0}+b-y_{0}\vert}{\sqrt{1 + a^2}}\]c’est-à-dire avec la notation habituelle \[d\left(P, \, D_{1}\right) = \frac{\vert ax_{0}+b-y_{0}\vert}{\sqrt{1 + a^2}}\]
Belle preuve :)