La formule de Héron nous permet de trouver l’aire d’un triangle quelconque connaissant les mesures de ses trois côtés. Il suffit de calculer d’abord le demi-périmètre du triangle , avec côtés , et , et ensuite de calculer Il existe de nombreuses preuves de ce résultat (en utilisant Pythagore ou un peu de trigonométrie) mais aucune n’est aussi belle que celle fournie par Héron même. Sa preuve se lit comme un bon roman : elle est ingénieuse, élégante et garde le lecteur en haleine jusqu’à ce que la finale se dévoile abruptement.
La preuve repose sur cinq résultats. On prend d’abord quelques minutes pour les apprécier.
Proposition 1 : les bissectrices d’un triangle se rencontrent en un point. C’est le centre du cercle inscrit dans le triangle.
La bissectrice est la droite qui coupe l’angle en deux angles isométriques. On considère l’angle suivant. On trace la bissectrice .
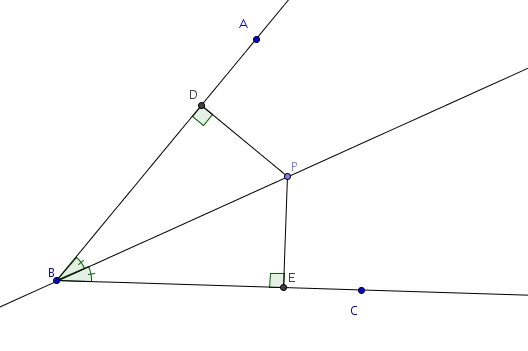
On doit montrer que tout point de la bissectrice est équidistant des côtés de l’angle. On trace les segments perpendiculaires à et passant par , respectivement et , et respectivement les distances de à et de à . Par définition de bissectrice, les angles et sont isométriques. Les angles et sont droits (et donc isométriques). Et comme la somme des mesures des angles intérieurs d’un triangle est toujours égale à 180°, on trouve que les angles et sont forcément isométriques eux-aussi. Les triangles et partageant tous les deux le côté , on trouve qu’ils sont isométriques par le cas ACA. Et comme dans les triangles isométrique les côtés homologues sont isométriques, on trouve que et sont isométriques. Le point est donc équidistant des deux côtés de l’angle.
La réciproque est aussi vraie. Si est équidistant de et de , alors on a que et sont isométriques. Les deux triangles et partagent le côté . Les deux triangles et sont rectangles (par définition de distance) et donc, avec Pythagore, on trouve que les segments et sont eux-aussi isométriques. Les triangles sont donc isométriques par le cas CCC et comme dans les triangles isométriques, les angles homologues sont isométriques, on conclut que les angles et sont isométriques. est donc une bissectrice.
On considère maintenant le triangle suivant, dans lequel on a tracé les bissectrices des angles et qui se croisent en .
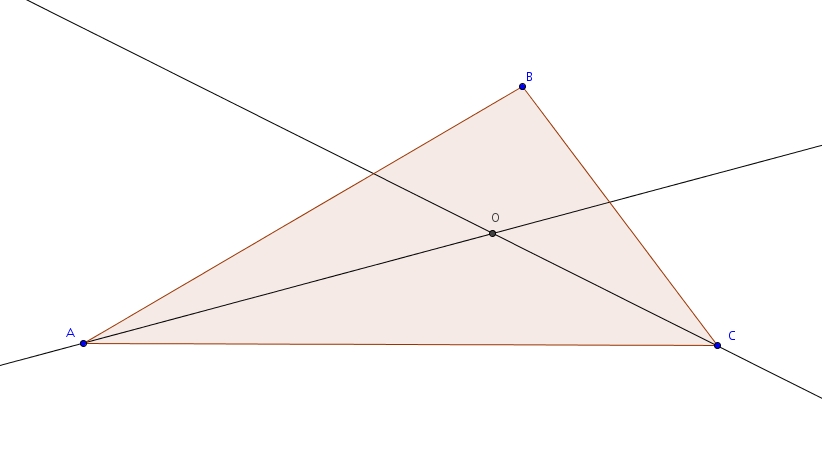 Puisque est sur la bissectrice de l’angle , il est équidistant des côtés et . Puisque est aussi sur la bissectrice de l’angle , il est équidistant des côtés et de . Par conséquent, il est donc aussi équidistant des côtés et . est donc aussi sur la bissectrice de l’angle . Les bissectrices se coupent en un point : c’est le centre du cercle inscrit. En effet, les distances de à , de à et de à , toutes égales, jouent le rôle de rayons de ce cercle, rayons perpendiculaires aux côtés du triangle (définition de distance). Les côtés du triangle sont donc tangents au cercle.
Puisque est sur la bissectrice de l’angle , il est équidistant des côtés et . Puisque est aussi sur la bissectrice de l’angle , il est équidistant des côtés et de . Par conséquent, il est donc aussi équidistant des côtés et . est donc aussi sur la bissectrice de l’angle . Les bissectrices se coupent en un point : c’est le centre du cercle inscrit. En effet, les distances de à , de à et de à , toutes égales, jouent le rôle de rayons de ce cercle, rayons perpendiculaires aux côtés du triangle (définition de distance). Les côtés du triangle sont donc tangents au cercle.
Proposition 2 : La hauteur issue de l’angle droit d’un triangle rectangle détermine deux petits triangles semblables entre-eux et aussi semblables avec le grand triangle de départ.
Cette proposition est vue en quatrième secondaire. On considère le triangle rectangle en suivant. On trace la hauteur .
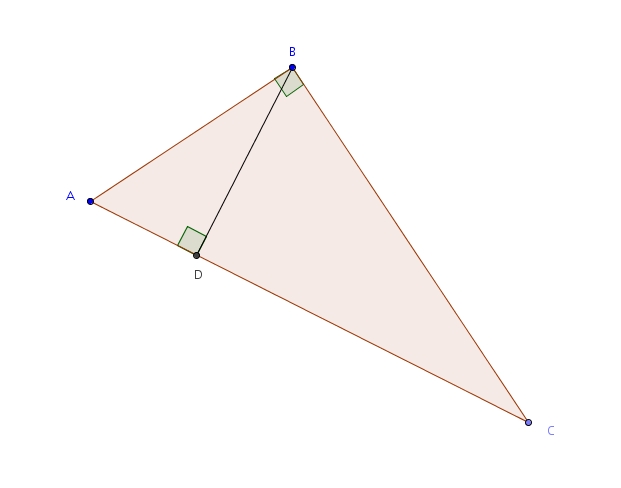
Par définition de hauteur, l’angle est droit et le triangle est rectangle. Les triangles et partagent l’angle , ils sont donc semblables par le cas de similitude AA.
Par définition de hauteur, l’angle est droit et le triangle est aussi rectangle. Les triangles et partagent l’angle et ils sont donc semblables par le cas de similitude AA.
Puisque les triangles et sont tous deux semblables au triangle , on conclut qu’il sont aussi semblables entre eux.
Proposition 3 : Dans un triangle rectangle, le milieu de l’hypoténuse est équidistant des trois sommets.
On considère le triangle rectangle en suivant. On trace le point milieu de . On trace ensuite la perpendiculaire à passant par . Cette perpendiculaire coupe en .
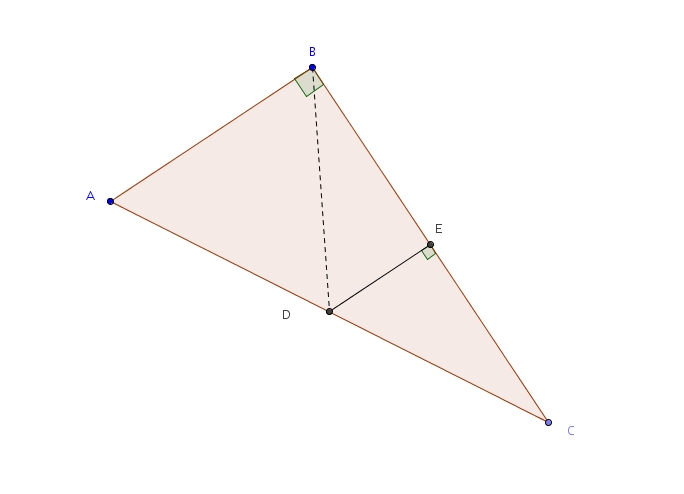 Il reste à montrer que , et sont isométriques. Comme est le point milieu de , on trouve que et sont isométriques. Les angles et sont également isométriques. Les triangles et partageant le même côté , on trouve qu’ils sont isométriques par le cas CAC. Et comme dans les triangles isométriques les côtés homologues sont isométriques, on trouve que et sont isométriques. La moitié du travail reste à faire.
Il reste à montrer que , et sont isométriques. Comme est le point milieu de , on trouve que et sont isométriques. Les angles et sont également isométriques. Les triangles et partageant le même côté , on trouve qu’ils sont isométriques par le cas CAC. Et comme dans les triangles isométriques les côtés homologues sont isométriques, on trouve que et sont isométriques. La moitié du travail reste à faire.
Par la suite, on remarque que Et comme l’angle est droit, on obtient d’abord puis Comme dans les triangles isométriques, les angles homologues sont isométriques, on trouve En remplaçant dans l’équation précédente, on obtient : Or, que vaut l’angle ? Tout simplement puisqu’il s’agit d’angles adjacents complémentaires. On obtient donc : Le triangle est donc isocèle et, par conséquent, les côtés et sont isométriques.
Proposition 4 : Si ABCD est un quadrilatère (avec les diagonales AC et BD) et que les angles BAC et BDC sont des angles droits, alors le quadrilatère est inscriptible dans un cercle (en d’autres mots, on peut tracer un cercle passant par ABCD).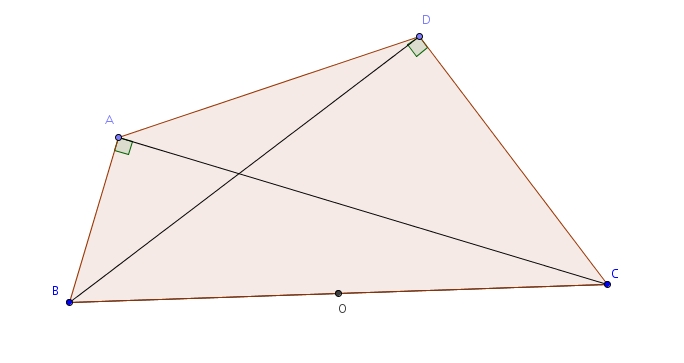 On trace , le milieu de . Les triangles et sont tous les deux rectangles et possède la même hypoténuse . Le point est le milieu de cette hypoténuse et, par la proposition 3, est donc équidistant de , de , de et de . On peut donc tracer un cercle de centre passant par , , , et .
On trace , le milieu de . Les triangles et sont tous les deux rectangles et possède la même hypoténuse . Le point est le milieu de cette hypoténuse et, par la proposition 3, est donc équidistant de , de , de et de . On peut donc tracer un cercle de centre passant par , , , et .
Proposition 5 : Les angles opposés d’un quadrilatère inscriptible dans un cercle sont supplémentaires.
On considère le quadrilatère inscrit dans le cercle de centre suivant :
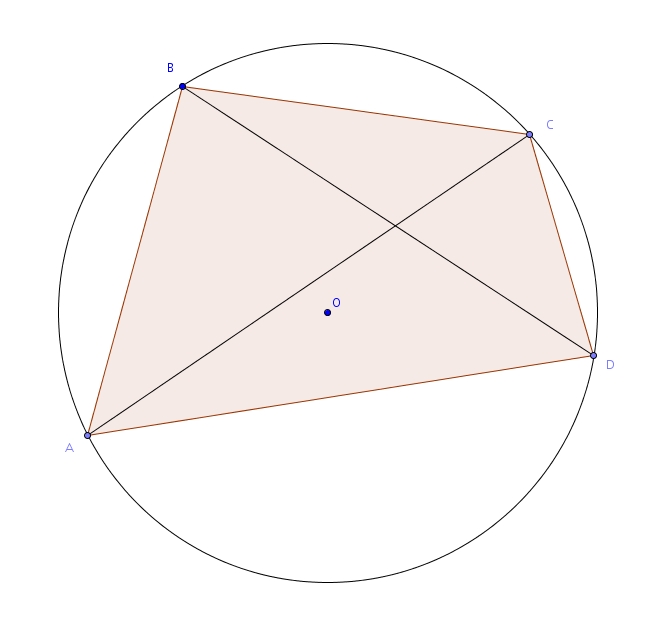 Dans le triangle , on trouve que Les angles et sont des angles inscrits qui interceptent le même arc . Ils sont donc isométriques. Les angles et sont des angles inscrits qui interceptent le même arc . Ils sont donc isométriques. En substituant, on obtient : Mais comme on obtient : Voilà !
Dans le triangle , on trouve que Les angles et sont des angles inscrits qui interceptent le même arc . Ils sont donc isométriques. Les angles et sont des angles inscrits qui interceptent le même arc . Ils sont donc isométriques. En substituant, on obtient : Mais comme on obtient : Voilà !
Il est fort possible, à ce moment, que vous trouviez que ces cinq propositions ne suggèrent rien qui puisse aider à trouver l’aire d’un triangle. Et pourtant ! C’est tout ce dont Héron avait besoin pour compléter sa longue et ingénieuse preuve !
On considère un triangle quelconque comme celui de la figure suivante. Par convention, on pose
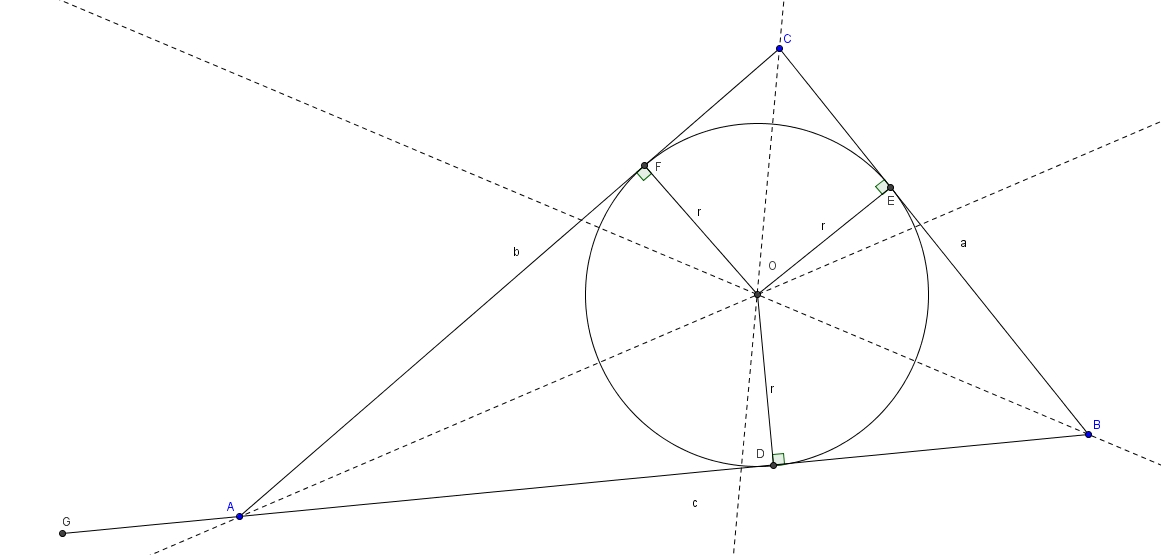
On trace les trois bissectrices des angles du triangle. Par la proposition 1, ces trois bissectrices se rencontrent en . Par la même proposition, on sait que est à égale distance des trois côtés du triangle : on appelle cette distance et on trace le cercle de centre et de rayon . Ce cercle est tangent à en , à en et à en . On a donc Enfin, puisqu’il apparait dans la formule de Héron, on pose comme le demi-périmètre Pour des raisons qui ne sont pas apparentes pour l’instant, on prolonge jusqu’à de telle sorte que Clairement, l’aire du triangle est égale à la somme des aires des trois triangles , et .
Avec la bonne vieille formule Héron trouve En posant et en remplaçant les aires par les expressions trouvées, il obtient En mettant en évidence, il trouve ensuite ou tout simplement
C’est remarquable puisqu’il fait déjà apparaitre le demi-périmètre dans la formule d’aire. Remarquable, certes, mais l’objectif final est encore très loin.
En se référant à notre figure, et en se rappelant que les bissectrices déterminent des angles isométriques, on découvre une panoplie de triangles isométriques. Par exemple, les triangles et possèdent déjà deux angles homologues isométriques (l’angle droit et celui formé par la bissectrice). Leur troisième angle homologue étant conséquemment isométrique (la somme des angles intérieurs d’un triangle vaut toujours ) et le côté étant partagé par les deux triangles, on affirme, par le cas d’isométrie ACA, que les triangles et sont isométriques. Héron trouve de la même manière Et comme dans les triangles isométriques les côtés et les angles homologues sont isométriques, il trouve aussi et À ce moment, Héron remarque que ce qui est égal à et donc ce qui fait, après quelques substitutions, Mais comme il avait défini au départ il trouve finalementce qui fait en réarrangeant les termes ou tout simplement La mesure du segment est donc égale au demi-périmètre ! Il semble que Héron voulait avoir ce segment devant les yeux avant de continuer. Cela dit, il déduit certaines mesures qui nous seront utiles sous peu. Il trouve d’abordHéron trouve ensuite ce qui faitpuis en remplaçantIl obtient doncou tout simplementEnfin, il trouvece qui faitet donc après substitution, Puisqueil obtient simplement Ces trois relations avec le demi-périmètre apparaissent dans la formule de Héron. Ils feront l’objet de substitutions lors d’une étape cruciale de la preuve.
On reprend maintenant notre figure initiale et on y ajoute quelques constructions. Héron trace perpendiculaire à . coupe en . Il trace ensuite perpendiculaire à par . On nomme le point d’intersection de et .
Le résultat de cette construction qui nous intéresse est le quadrilatère . Puisque les diagonales et sont perpendiculaires aux côtés et , on déduit, par la proposition 4, qu’il s’agit d’un quadrilatère inscriptible dans un cercle. Par la proposition 5, on peut aussi affirmer que ses angles opposés sont supplémentaires. On a donc Héron porte ensuite son attention sur les angles autour de . Afin de rendre le tout plus facile à lire, on pose
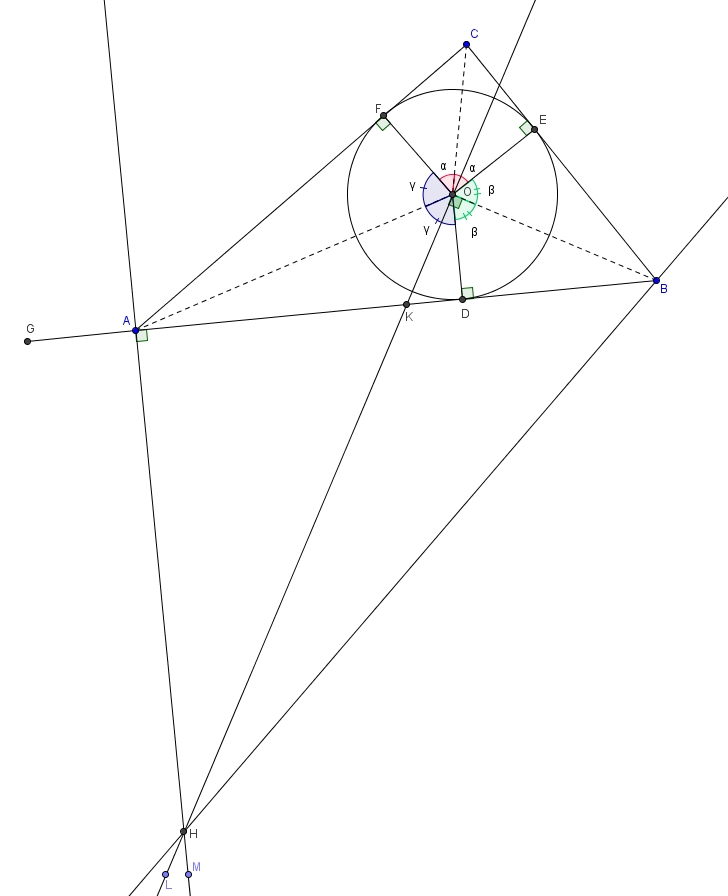
Il obtient facilement l’égalité suivante et en divisant chaque côté par , Mais comme il substitue pour obtenir Et puisque il trouve Cette dernière égalité reste particulièrement intéressant puisqu’elle nous permet d’énoncer une nouvelle paire de triangle semblables, à savoir les triangles et puisqu’ils sont aussi tous les deux rectangles (cas de similitude AA).Et comme dans les triangles semblables, les côtés homologues sont dans le même rapport, Héron établit la proportion suivante : En intervertissant les extrêmes, il obtient cette égalité Les angles et sont opposés par le sommet et donc isométriques. Héron établit donc la similitude des triangles et , en utilisant le cas AA puisque les deux triangles comportent aussi un angle droit. Il obtient ainsi cette deuxième proportion importante En intervertissant les extrêmes, il obtient Et en combinant l’équation précédente et celle-ci il obtient Mais Héron n’a pas encore terminé avec les triangles semblables ! Il s’attaque au triangle rectangle et sa hauteur . Par la proposition 2, on sait que les triangles et sont semblables. Héron établit donc cette (autre) proportion que l’on peut réécrire, si on le préfère, comme Héron reprend ensuite et ajoute de chaque côté En mettant sur dénominateur commun et en effectuant l’addition, il obtient ce qui n’est autre que Héron multiplie le côté gauche de l’équation par et le côté droit de l’équation par Il obtientOr, puisque il remplace et obtientque l’on peut enfin réécrire Ah ha ! Rappelons nous que Héron avait plus haut trouvé Et donc en remplaçant, il trouve En extrayant la racine carrée et en réarrangeant l’ordre des facteurs, il trouve finalement Et comme il avait il lui suffit d’écrire Magnifique !
Référence : William Dunham (1991), Journey Through Genius
 Puisque
Puisque  Il reste à montrer que
Il reste à montrer que  On trace
On trace  Dans le triangle
Dans le triangle 



Comme j’aime ce blogue.
J’aurais une petite question : avec quel logiciel réalises-tu tes graphiques ?
Avec Géogébra.
http://www.geogebra.org
C’est gratuit et libre et vraiment génial (on oublie rapidement Cabri et tous les autres). Il suffit d’avoir JAVA (gratuit aussi) d’installé.
Bonne journée !
Merci !
Merci beaucoup pour cette splendide démonstration !
Tout le plaisir est mien !
Ah ! Ces trucs vieux de 2000 ans…