La résolution d’un polynôme du deuxième degré

Le mathématicien arabe Al-Khawarizmi résout dans son livre paru en 825 et intitulé kitāb al-mukhtaṣar fī ḥisāb al-jabr wa’l-muqābalah (abrégé du calcul par la restauration et la comparaison) des équations du deuxième degré.  Notez que le terme al-jabr du titre nous donnera plus tard le mot algèbre.

On peut résoudre ces équations, et faire la démonstration de la formule quadratique en « complétant le carré ». Voici donc une telle démonstration avec, en prime, et comme au temps d’Al-Khawarizmi, un support géométrique. On a donc $$a{x}^2+bx+c=0$$On divise chaque terme par $a$ $$x^2+\frac{b}{a}x+\frac{c}{a}=0$$et on complète le carré  : c’est à dire rajouter une quantité qui fera en sorte que les trois premiers termes constituerons un trinôme carré parfait.  Évidemment, il faut aussi retrancher immédiatement cette quantité afin de ne pas changer la valeur du polynôme.  Quelle est cette quantité ?  Les deux premiers termes, étant ceux qui nous intéressent, sont représentés dans l’illustration suivante 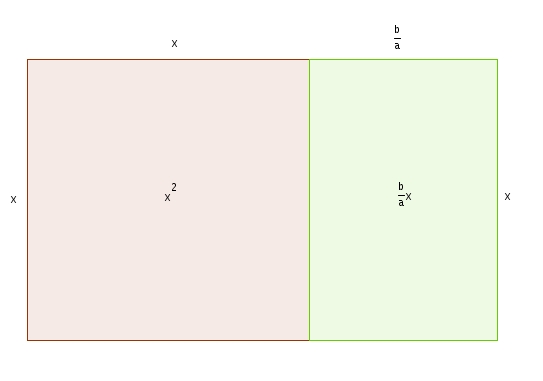En séparant le rectangle vert en deux rectangle isométriques et en réarrangeant les pièces, on obtient

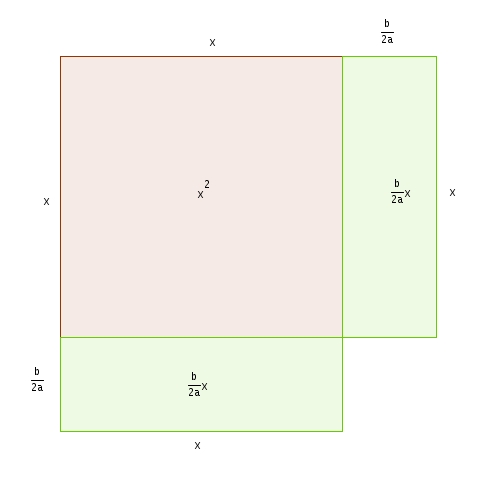On se rend compte qu’il nous sera possible de compléter le carré faut en ajoutant $${\left(\frac{b}{2a}\right)}^2$$tel qu’illustré dans le diagramme suivant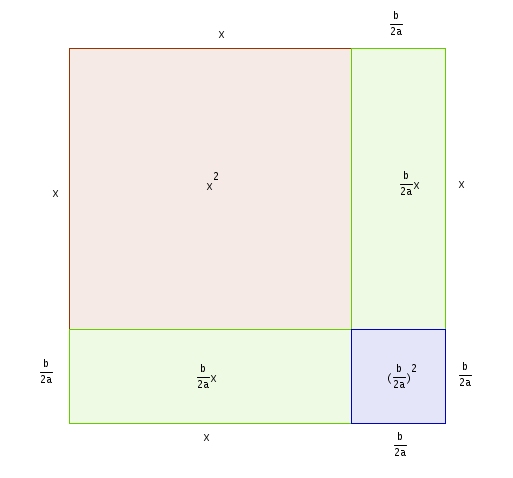

On se retrouve ainsi avec un carré dont les côtés mesurent $$x+\frac{b}{2a}$$Enfin bref, on a $$x^2+\frac{b}{a}x+{\left(\frac{b}{2a}\right)}^2-{\left(\frac{b}{2a}\right)}^2+\frac{c}{a}=0$$
ou $$x^2+\frac{b}{a}x+\frac{b^2}{4a^2}-\frac{b^2}{4a^2}+\frac{c}{a}=0$$Il est possible de factoriser le trinôme carré parfait $${(x+\frac{b}{2a})}^2-\frac{b^2}{4a^2}+\frac{c}{a}=0$$On isole ensuite le carré $${(x+\frac{b}{2a})}^2=\frac{b^2}{4a^2}-\frac{c}{a}$$On met ensuite les termes de droite sur dénominateur commun $${(x+\frac{b}{2a})}^2=\frac{b^2}{4a^2}-\frac{4ac}{4a^2}$$ce qui nous permet d’écrire $${(x+\frac{b}{2a})}^2=\frac{b^2-4ac}{4a^2}$$Il suffit maintenant d’extraire la racine carrée de chaque côté $$x+\frac{b}{2a}=\pm \sqrt{\frac{b^2-4ac}{4a^2}}$$Et là une propriétés des racines nous permet d’écrire ceci $$x+\frac{b}{2a}=\frac{\pm \sqrt{b^2-4ac}}{\sqrt{4a^2}}$$afin de simplifier comme cela$$x+\frac{b}{2a}=\frac{\pm \sqrt{b^2-4ac}}{2a}$$Il suffit enfin d’isoler $x$ $$x=-\frac{b}{2a}\pm \frac{\sqrt{b^2-4ac}}{2a}$$ce qui fait $$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$Le but de ce distrayant billet est de présenter une deuxième technique : le changement de variable.  On sait que si notre équation ne comporte qu’un terme au carré, par exemple $$x^2=c$$on n’a qu’à extraire la racine carrée des deux côtés afin d’obtenir $$x=\pm \sqrt{c}$$soit les solutions de l’équation.  C’est en quelque sorte une situation idéale.  C’est donc le terme du premier degré qui cause problème.  Il est possible d’éliminer ce terme avec un changement de variable.  Nous avons donc à nouveau $$a{x}^2+bx+c=0$$On divise ensuite chaque terme par $a$ $$x^2+\frac{b}{a}x+\frac{c}{a}=0$$Et là on effectue le changement de variable suivant $$x=y-\alpha$$ce qui fait $${(x-\alpha )}^2+\frac{b}{a}(y-\alpha )+\frac{c}{a}=0$$En développant on obtient $$y^2-2\alpha y+{\alpha }^2+\frac{b}{a}y-\frac{b}{a}\alpha +\frac{c}{a}=0$$puis en regroupant les termes semblables $$y^2+\frac{b}{a}y-2\alpha y+{\alpha }^2-\frac{b}{a}\alpha +\frac{c}{a}=0$$La mise en évidence de $y$ donne $$y^2+(\frac{b}{a}-2\alpha )y+{\alpha }^2-\frac{b}{a}\alpha +\frac{c}{a}=0$$L’objectif du changement de variable est d’éliminer le terme en $y$.  Posons$$\frac{b}{a}-2\alpha =0$$Il suffit d’isoler $\alpha$ $$-2\alpha =-\frac{b}{a}$$puis $$\alpha =\frac{b}{2a}$$C’est cette valeur qui fera disparaître le terme du premier degré dans l’équation précédente.  Remplaçons $$y^2+(\frac{b}{a}-2\left(\frac{b}{2a}\right))y+{\left(\frac{b}{2a}\right)}^2-\frac{b}{a}\left(\frac{b}{2a}\right)+\frac{c}{a}=0$$En multipliant les parenthèses on obtient $$y^2+(\frac{b}{a}-\frac{2b}{2a})y+\frac{b^2}{4a^2}-\frac{b^2}{2a^2}+\frac{c}{a}=0$$puis en simplifiant un peu $$y^2(\frac{b}{a}-\frac{b}{a})y+\frac{b^2}{4a^2}-\frac{b^2}{2a^2}+\frac{c}{a}=0$$On obtient ce qui était attendu$$y^2+(0)y+\frac{b^2}{4a^2}-\frac{b^2}{2a^2}+\frac{c}{a}=0$$En mettant sur dénominateur commun $$y^2+\frac{b^2}{4a^2}-\frac{2b^2}{4a^2}+\frac{4ac}{4a^2}=0$$on obtient $$y^2+\frac{-b+4ac}{4a^2}=0$$Puis en isolant $y^2$ $$y^2=\frac{b^2-4ac}{4a^2}$$et en extrayant la racine carrée de chaque côté de l’égalité $$y=\pm \sqrt{\frac{b^2-4ac}{4a^2}}$$Un propriété des racines nous permet d’écrire $$y=\frac{\pm \sqrt{b^2-4ac}}{\sqrt{4a^2}}$$puis de simplifier $$y=\frac{\pm \sqrt{b^2-4ac}}{2a}$$Or, on avait posé $$x=y-\alpha$$avec$$\alpha =\frac{b}{2a}$$En remplaçant on obtient $$x=y-\frac{b}{2a}$$et donc $$x+\frac{b}{2a}=y$$Il suffit maintenant de substituer $y$ dans $$y=\frac{\pm \sqrt{b^2-4ac}}{2a}$$ce qui donne$$x+\frac{b}{2a}=\frac{\pm \sqrt{b^2-4ac}}{2a}$$et donc $$x=-\frac{b}{2a}\pm \frac{\sqrt{b^2-4ac}}{2a}$$Or comme les deux termes sont déjà sur dénominateur commun, on obtient finalement $$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$La méthode semble fastidieuse dans ce contexte relativement simple.  Mais c’est cette méthode qui est utilisée dans la résolution d’un polynôme du troisième degré.  Il est donc préférable d’en avoir pleine compréhension avant de se lancer dans l’entreprise éminemment plus complexe qu’est la résolution d’un polynôme du troisième degré.