L’astroïde est la trace du point P d’un cercle de rayon R/4 qui roule sans glisser à l’intérieur d’un cercle de rayon R.
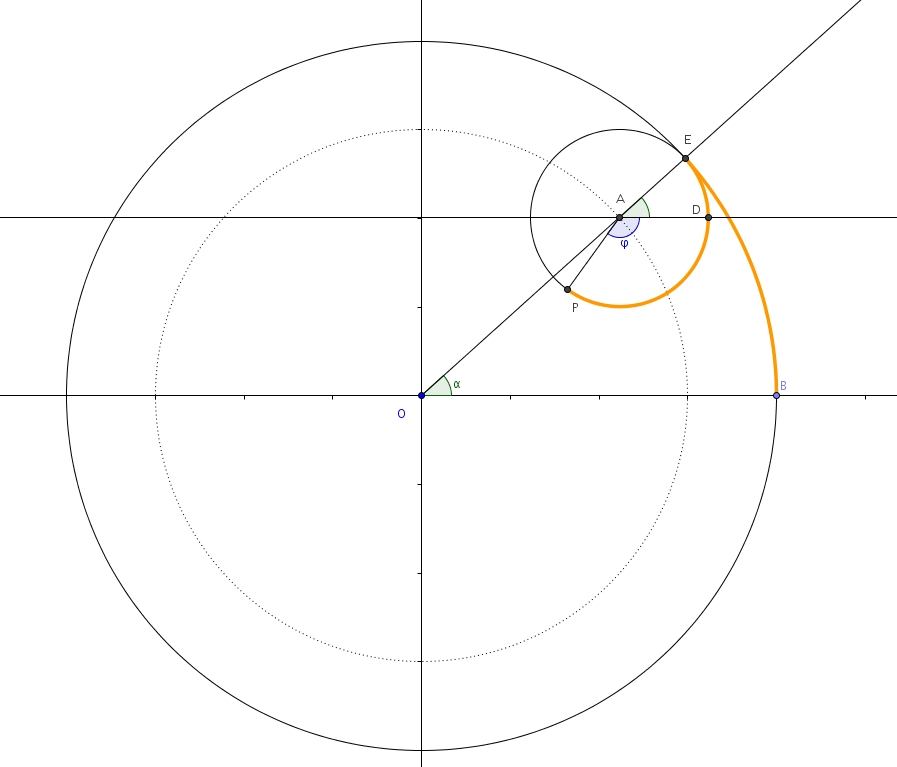
Sur la figure : le grand cercle rayon OB, de centre O, le petit cercle rayon AP, de centre A, avec
qui roule sans glisser à l’intérieur du grand cercle. On considère la trace du point P. On remarque que le centre A du petit cercle décriera une trajectoire telle qu’un cercle de rayon
et de centre O (en pointillé sur la figure). Le point E est le point de tangence entre les petit et grand cercles.
L’angle α est l’angle que forme le centre A du petit cercle, le centre O du grand cercle et l’axe des abscisses (en vert sur la figure, l’angle AOB, calculé dans le sens habituel, anti-horaire). En traçant la droite AD parallèle à l’axe, on obtient des angles correspondants isométriques. L’angle EAD a donc lui aussi pour mesure α. En posant
calculé dans le sens horaire, on obtient
En posant enfin
on peut trouver les coordonnées du point A
et celles de P
ou en effectuant la mise en évidence :
(Remarquez que, les angles étant orientés, α dans le sens anti-horaire et φ dans le sens horaire, on additionne R/4 cos(φ) à l’abscisse et on soustrait R/4 sin(φ) à l’ordonnée.)
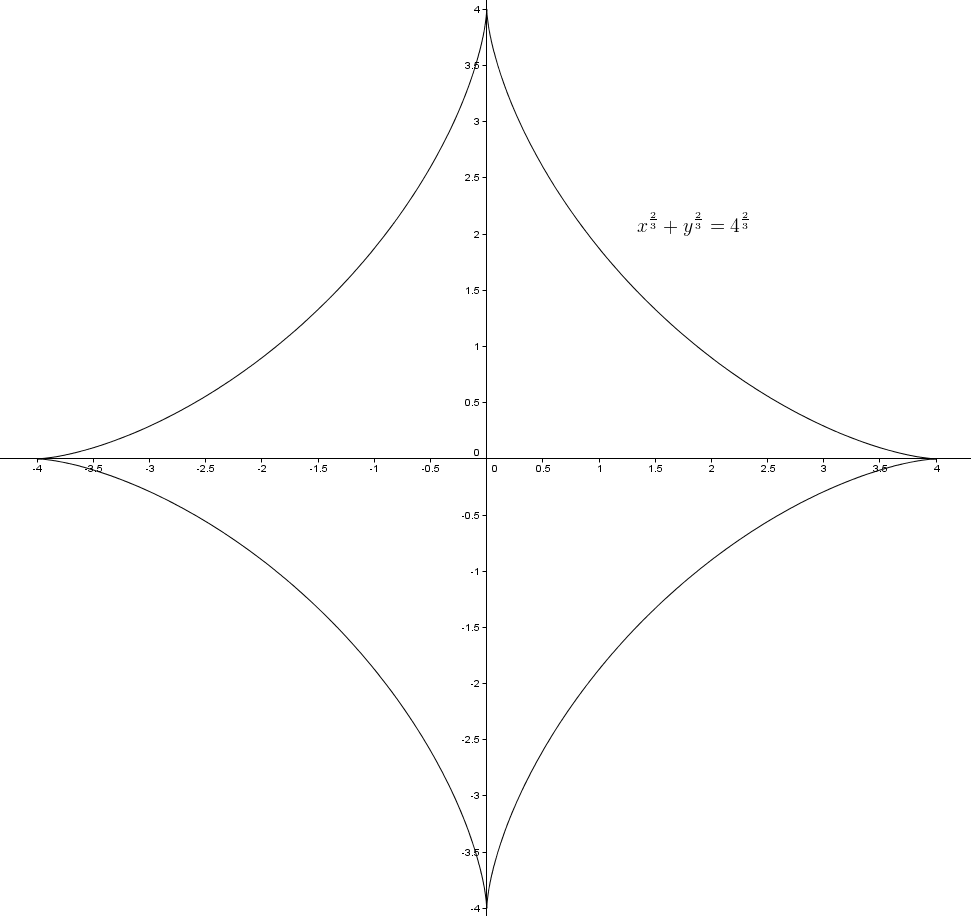
Comme le cercle roule sans glisser, on trouve aussi que les mesures des arcs EB et EDP sont égales. On a
et
Cela nous permet d’écrire
ce qui fait
et donc
Il nous est donc possible de réécrire l’expression pour les abscisses
et les ordonnées 
du point point P de l’astroïde en fonction de α. On obtient
et
Or, comme
et
on peut substituer les expressions cos(3α) et sin(3α) dans les équations précédentes. On obtient pour les abscisses
ce qui se simplifie d’abord à
puis à
On obtient pour les ordonnées
ce qui fait d’abord
puis
et enfin tout simplement
Les équations
et
sont les équations paramétriques de l’astroïde. On peut trouver la forme cartésienne générale comme suit. Dans l’équation des abscisses, on divise les deux côtés par R
puis on prend la racine cubique
que l’on peut aussi écrire
On élève au carré :
ce qui fait
On procède ensuite avec les ordonnées, en divisant par R
puis en prenant la racine cubique
ce qui fait
On élève au carré
que l’on peut aussi réécrire comme
Il suffit enfin de ressortir notre bonne vieille identité trigonométrique
et de judicieusement remplacer
et
et obtenir 
En multipliant chaque terme par 
, on obtient l’équation cartésienne générale
dont voici la représentation graphique
