On a deux villes, \(A\) et \(B\), de part et d’autre de la rivière. On veut relier ces villes par une voie rapide et un pont. Étant donnés les contraintes inhérentes à la construction d’un pont et les coûts associés, celui-ci est perpendiculaire aux rives.
Comment relie-t-on les villes pour que la distance soit minimale ?
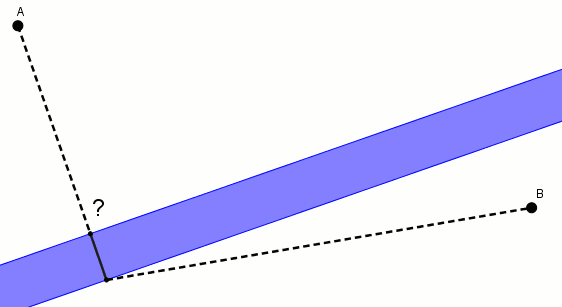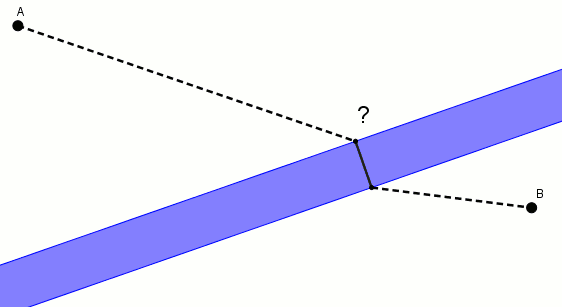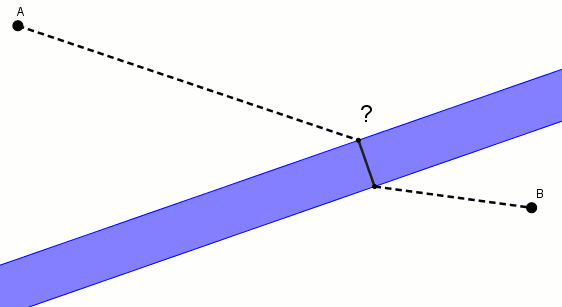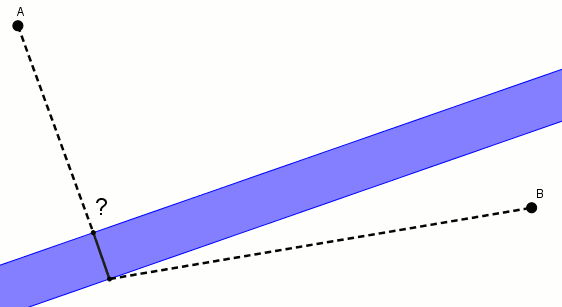
Le problème semble difficile. Avec des données, on peut y aller numériquement (à l’aide d’un ordinateur, en plus, c’est amusant à faire). On peut aussi ajouter un repère cartésien et utiliser le calcul différentiel, mais les expressions algébriques à manipuler deviennent vite embêtantes.
La translation, à quoi ça sert ?
Voici une solution fort jolie. On considère une flèche de translation perpendiculaire à la rive et dont la longueur correspond à la largeur de la rivière. On effectue la translation de \(A\) par cette flèche de translation. On obtient \(A’\). On relie \(A’\) et \(B\) par un segment qui coupe les deux rives.
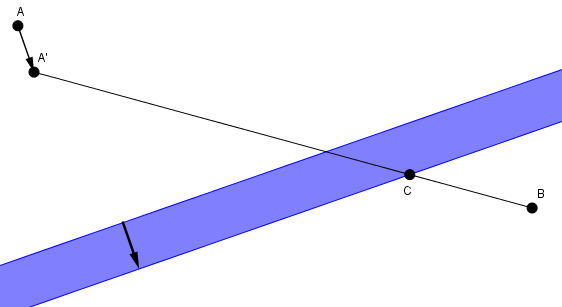
\(\overline{A’B}\) coupe la rive la plus près de \(B\) en \(C\). C’est l’endroit où l’on doit construire le pont. On nomme l’autre extrémité du pont \(M\) et on peut prétendre que le chemin \(AMCB\) est le plus court.
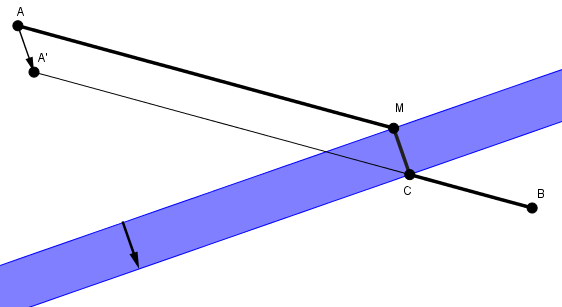
En effet, par construction \(\overline{AA’}\) et \(\overline{MC}\) sont isométriques et parallèles, et le quadrilatère \(AMCA’\) est un parallélogramme. Comme les côtés opposés du parallélogramme sont isométriques, on a en plus \[\overline{AM}\ \cong\ \overline{A’C}\]
Ainsi, \[m\overline{AM}\ +\ m\overline{CB}\ =\ m\overline{A’C}\ +\ m\overline{CB}\]et comme \(A\), \(C’\) et \(B\) sont colinéaires, cette mesure est minimale !
La stratégie s’applique aussi bien avec plusieurs rivières.
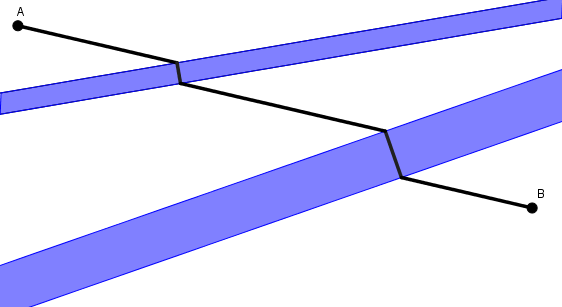
C’est joli, mais cela demande aussi un peu de génie. Pour un peu de simplicité, on considère deux rivières et on suppose le problème résolu : les deux ponts à construire sont \(\overline{DF}\) et \(\overline{CE}\).
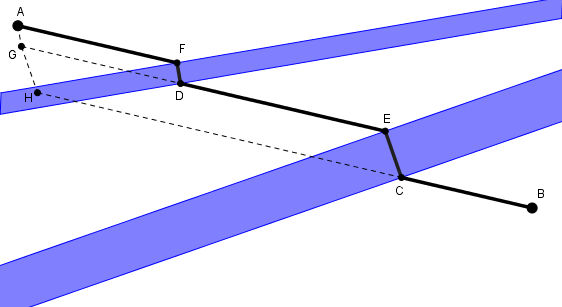
On effectue la translation de \(\overline{DF}\) jusqu’à \(\overline{GA}\) de telle sorte que \(F\) soit envoyé sur \(A\) (et \(D\) envoyé sur \(G\)). Ainsi, \(\overline{AF}\ \cong\ \overline{GD}\) et \[m\overline{AF}\ +\ m\overline{DE}\ +\ m\overline{CB}\ = \ m\overline{GD}\ + \ m\overline{DE}\ + \ m\overline{CB}\]
Si \(AFDECB\) est le plus court chemin menant de \(A\) à \(B\), alors \(GDECB\) sera le plus court chemin menant de \(G\) à \(B\) et \(DECB\) le plus court chemin menant de \(D\) à \(B\). Comme \(D\) et \(B\) ne sont séparés que par la deuxième rivière, on peut appliquer ce qu’on a trouvé dans le problème précédent !
Pour obtenir la solution, voici donc comment procéder. On trouve d’abord \(G\) en effectuant la translation de \(A\). La flèche de translation est perpendiculaire et en direction de la première rivière et sa longueur correspond à la largeur de celle-ci. Du point \(G\) on trouve \(H\) avec une autre translation dont la flèche de translation est perpendiculaire et en direction de la deuxième rivière et sa longueur correspond à la largeur de celle-ci. On relie \(H\) et \(B\) avec un segment qui coupe la rivière en \(C\) de la rive la plus près de \(B\) : c’est l’endroit où on construit le premier pont. Soit \(E\) l’autre extrémité du pont. On construit la parallèle à \(HB\) passant par \(E\). Cette parallèle coupe l’autre rivière en \(D\), de la rive la plus près de \(B\). C’est l’endroit où l’on doit construire l’autre pont.
Référence : Yaglom, I. M., Geometric Transformations I, MAA 1975