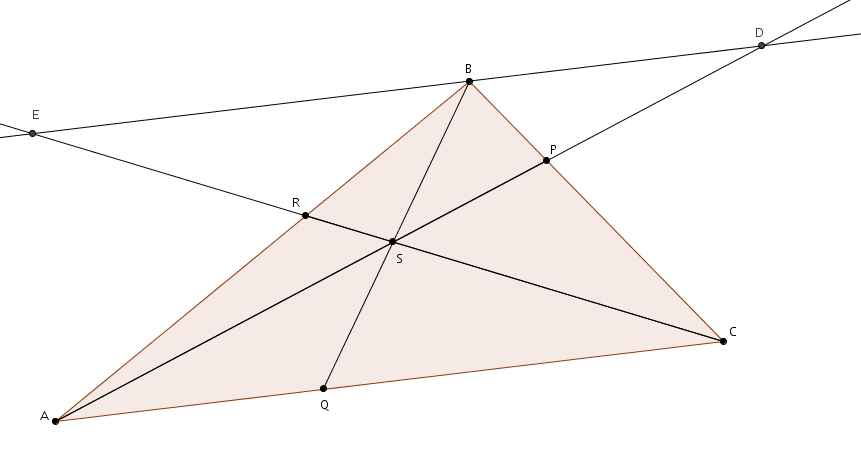
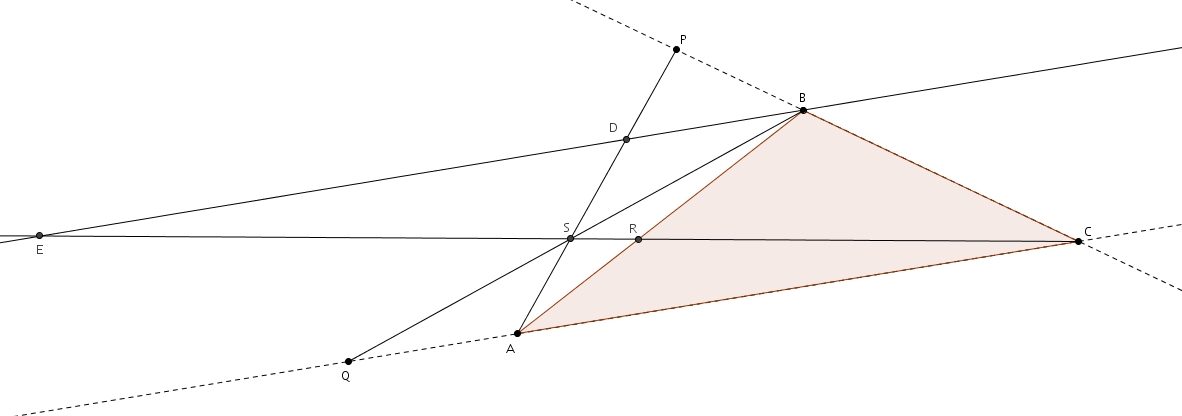
Le théorème de Ceva concerne les segments reliant sommets et côtés opposés dans les triangles.
Le théorème de Ceva…
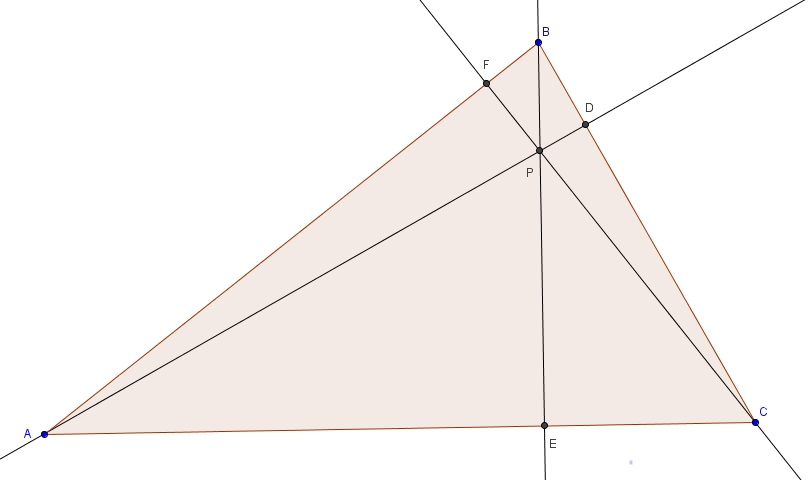
Considérons le triangle 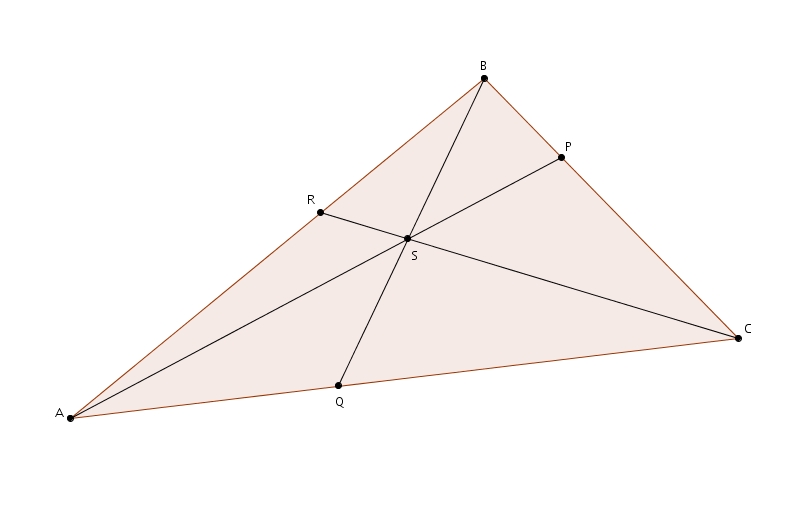
Plaçons
- 1. Les angles
- 2. Les angles
- 3. Les angles
- 4. Enfin, les angles
Grâce à 3 et 4, on tire
… et sa réciproque
Supposons que les segments
Or, si les segments
Les points
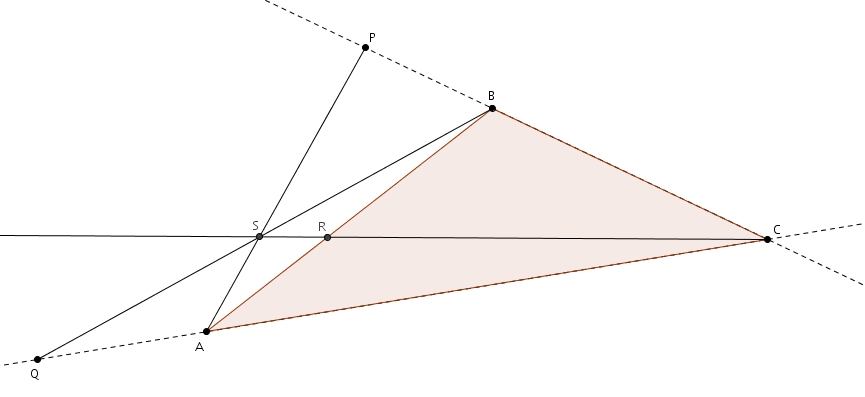 On trace la parallèle à
On trace la parallèle à
Tout le raisonnement ci-haut reste valide.
Le théorème de Ceva peut se trouver très utile lorsque vient le temps de fournir la preuve que des segments dans un triangle se rencontrent en un point. Dans ce billet et ce celui-ci on prouve que les médianes, les hauteurs et les bissectrices d’un triangle sont concourantes. Nous allons revisiter ces preuves avec le théorème de Ceva. Il s’avère que le travail sera beaucoup moins fastidieux.
Les médianes
Dans un triangle 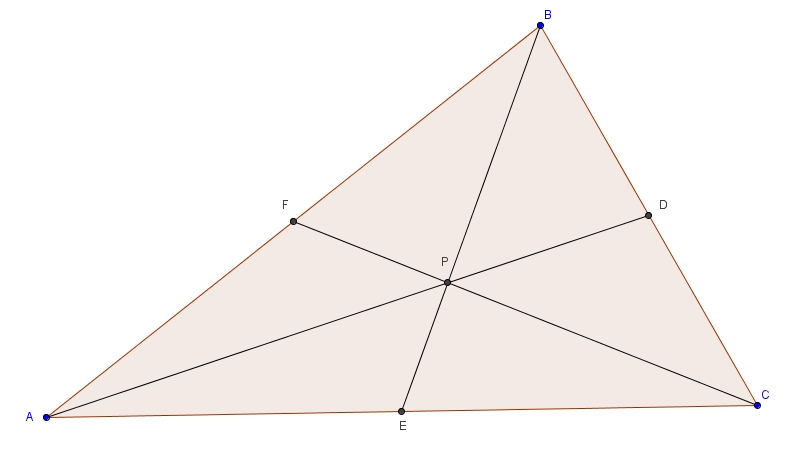 Par définition même de médiane, on sait que
Par définition même de médiane, on sait que
Les hauteurs
Dans le triangle
Les triangles
Les bissectrices
Dans le triangle
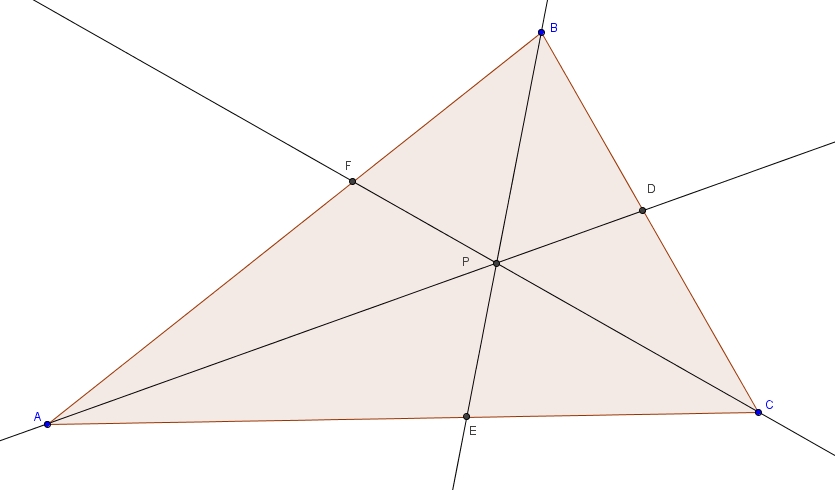 Dans un triangle, les bissectrices divisent toujours le côté opposé en deux segments proportionnels aux côtés de l’angle. Il suffit donc de tirer, avec, respectivement, les bissectrices
Dans un triangle, les bissectrices divisent toujours le côté opposé en deux segments proportionnels aux côtés de l’angle. Il suffit donc de tirer, avec, respectivement, les bissectrices
Référence : Alfred S. Posamentier et Charles T. Salkind (1996), Challenging Problems In Geometry