Lorsque les diagonales se croisent

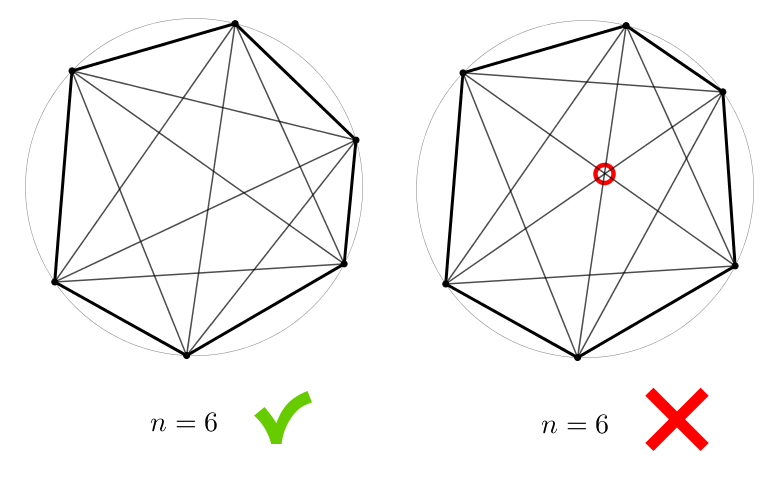
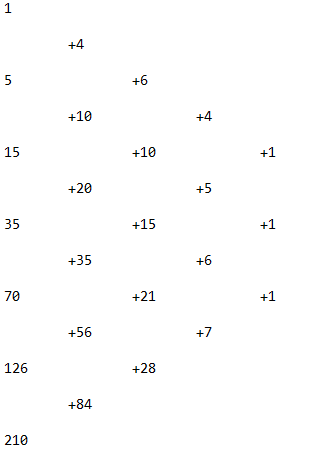On place $n$ points sur la circonférence d’un cercle pour former un polygone à $n$ côtés tout en s’assurant qu’il n’y ait pas trois de ses diagonales ou plus qui se coupent en un même point.

Un classique

Combien y a-t-il de diagonales dans un tel polygone à $n$ côtés ?

Une diagonale relie deux sommets qui ne sont pas adjacents. Pour tracer toutes les diagonales du polygone, on relie chaque sommet à tous les autres sommets, sauf trois : on ne peut relier un sommet à lui-même et aux deux sommets qui lui sont adjacents (en fait le sommet est déjà relié aux deux sommets qui lui sont adjacents par deux des côtés du polygone). Puisqu’il y a $n$ sommets et que chaque sommet est relié à $n-3$ autres sommets, on pourrait croire qu’il y a $n(n-3)$ diagonales mais on ferait erreur. Chaque diagonale a deux extrémités, elle relie deux sommets. L’expression $n(n-3)$ compte donc les diagonales en double. On a plutôt $$\text{nombre de diagonales}=\frac{n(n-3)}{2}$$Génial non ? 

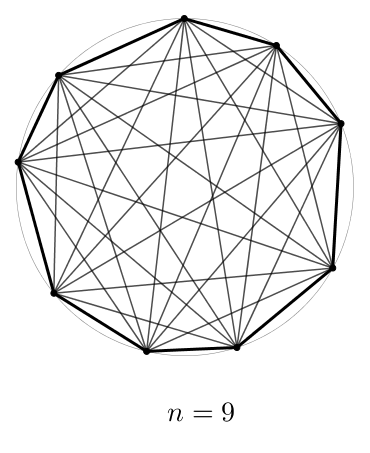
Dans le polygone ci-dessus à $9$ côtés, inutile de compter les diagonales une par une : il y en a $$\frac{9(9-3)}{2}=\frac{9\cdot 6}{2}=27$$

La suite

Combien y a-t-il de points d’intersection formés par les diagonales ?

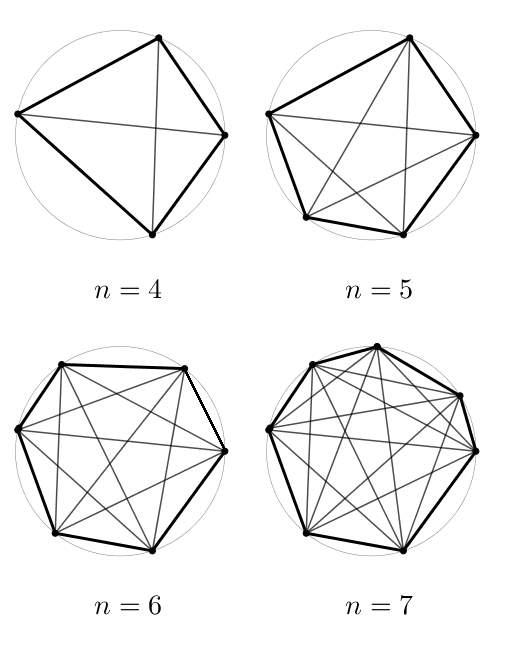
Hmmm… là, ça semble moins évident. Combien de points d’intersection ces diagonales forment-elles en effet ? Lorsque j’ai donné ce problème à un collègue, il s’est empressé de faire ce que tout bon matheux fait : étudier d’abord les petits cas, consigner les données et y chercher une régularité.

Nombre de côtés $n$	Nombre de points d'intersection formés par les diagonales
4	1
5	5
6	15
7	35
8	70
9	126
...	...

Je dois avouer que pour ma part, ces nombres ne me disaient pas grand chose. Une petite analyse des accroissements semble éventuellement révéler un polynôme de degré 4 [1].

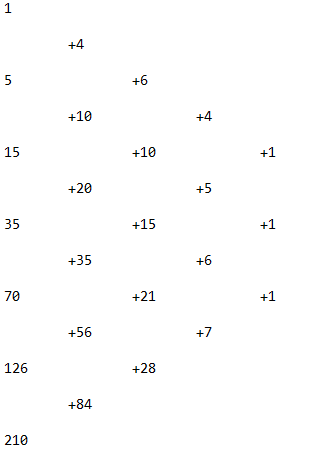
Mais en tant que fin amateur du triangle de Pascal, mon collègue a tout de suite remarqué ceci : 

 

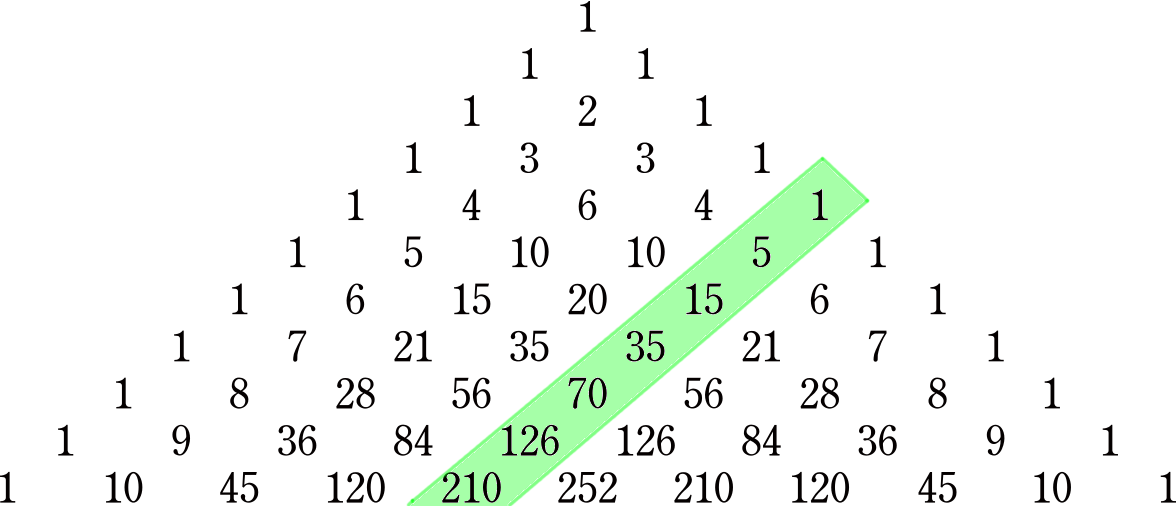
Comment cela pourrait-il nous aider à découvrir la solution ? En comptant à partir du 0^e étage du triangle, l’allée verte apparaît pour la première fois seulement au quatrième étage. Ce n’est peut-être pas si surprenant sachant que les triangles n’ont pas de diagonales et qu’on ne peut considérer des polygones à $0$, $1$ ou $2$ côtés. Considérant ensuite que les entrées du triangle correspondent aux coefficients binomiaux, le premier $1$ vert peut être interprété comme le nombre de façons de choisir sans répétition et sans ordre $4$ éléments dans un ensemble de $4$ éléments. Le $5$ vert qui suit, au cinquième étage, correspond au nombre de façons de choisir sans répétition et sans ordre $4$ éléments dans un ensemble de $5$ éléments. Le $15$ vert qui suit correspond au nombre de façon de choisir sans répétition et sans ordre $4$ éléments dans un ensemble de $6$ éléments. Et ainsi de suite… Comment tout cela se traduit-il géométriquement ? 

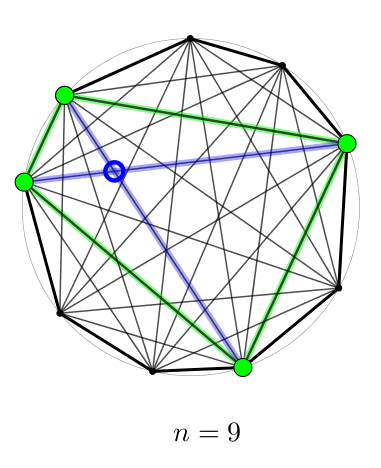
Si on choisit quatre sommets parmi les $n$ sommets du polygone, on forme un quadrilatère. Ce quadrilatère possède deux diagonales qui se coupent ! Bien sûr, les diagonales du quadrilatère appartiennent aussi au polygone à $n$ côtés. Et chaque couple de diagonales du polygone à $n$ côtés, qui définissent chaque point d’intersection, appartient à un quadrilatère unique. Ainsi, le nombre de points d’intersection des diagonales correspond au nombre de quadrilatères qu’il est possible de former avec les $n$ sommets. En d’autres mots, c’est le nombre de façons de choisir sans répétition et sans ordre $4$ sommets dans un ensemble de $n$ sommets. $$\begin{array}{rl}\text{nombre de points d’intersection}& =(\genfrac{}{}{0ex}{}{n}{4})\\ \\ & =\frac{n!}{4!(n-4)!}\end{array}$$

 

[1]  Pour les curieux, le polynôme en question est $$\frac{1}{24}(n^4-6n^3+11n^2-6n)$$