The Dude Minds…

Plus tôt cette année, un peu avant la journée de $\pi$, j’ai vu dans une infolettre mathématique hebdomadaire cette rubrique :

Je dois avouer que l’infolettre est d’ordinaire assez bien ficelée et que je trouve les contenus souvent intéressants et pertinents, surtout pour un enseignant au secondaire. Sans surprise j’étais donc enthousiasmé par la suite présentée, une suite simple, nouvelle en ce qui me concerne, et qui tend vers une constante célébrée. Je l’ai donc soumise avec entrain à certains élèves qui étaient encore dans la classe au moment où j’ai consulté l’infolettre. J’ai même osé dire à un élève dont je savais les parents professeurs de mathématiques : « Tiens, tu montreras ça à ton père ! Je ne sais pas encore pourquoi ça tend vers $\pi$, mais c’est intriguant ! »

Curieux de connaître la rapidité avec laquelle la suite converge vers $\pi$, en arrivant à la maison j’ai concocté un petit script en python :

Aïe aïe aïe ! J’ai été surpris de constater qu’en réalité la suite ne tend pas vers $\pi$, malgré ce qu’insinuait l’infolettre. Elle semble tendre vers un autre nombre pas loin, à près de $0,00005$ de $\pi$. Close, but no cigar. Oups ! Un petit courriel plus tard pour expliquer mon trop plein d’enthousiasme (et la bévue) au père de mon élève, et je me mettais au travail. « … numbers that converge to a recognisable number ». Ah ? Lequel ? Je ne vois pas.

Feu l’Inverseur de Plouffe

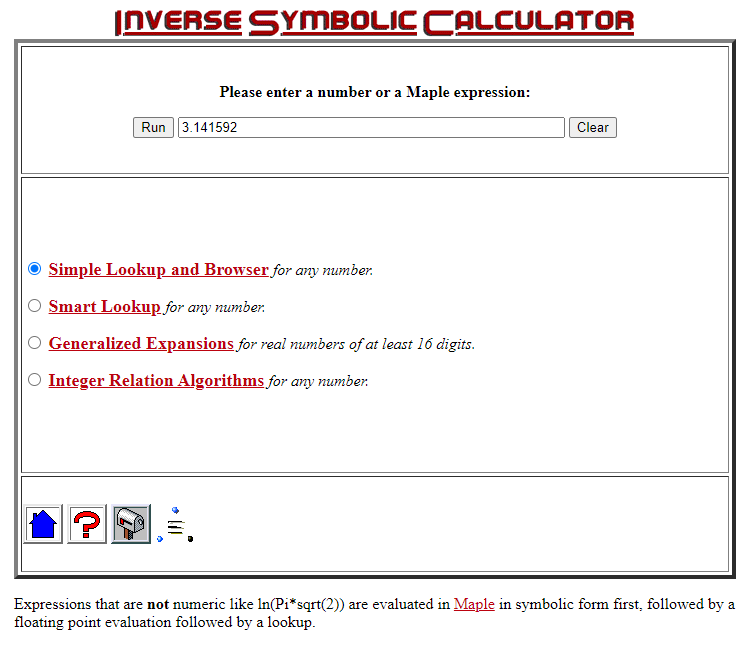
Étant incapable d’utiliser à bon escient la référence du Journal of Recreational Mathematics, mon premier réflexe a été de tenter de me rendre sur le site de l’Inverseur de Plouffe, pour voir si ce nombre mystère s’y trouvait. Je dis « tenter » car c’est à ce moment que j’ai découvert que l’Inverseur de Plouffe n’est plus en ligne… depuis… 12 ans. Re-oups. Ça ne nous rajeunit pas, disons.

La fraction médiane ? (non)

Je dois avouer que j’ai ensuite passé un peu (trop) de temps à investiguer du côté des fractions médianes. La fraction médiane de $\frac{a}{b}$ et $\frac{c}{d}$ est $\frac{a+c}{b+d}$. Et dans la suite, on somme les dividendes (numérateurs) et les diviseurs (dénominateurs) des deux termes précédents. On note parfois $\oplus$ l’opération de faire la somme des numérateurs et des dénominateurs $$\frac{a}{b}\oplus \frac{c}{d}=\frac{a+c}{b+d}$$que les anglophones nomment « the freshman’s sum » parce qu’il s’agit d’une façon erronée d’effectuer l’addition (traditionnelle) de fractions, erreur que répètent parfois certains élèves novices. L’intérêt de la fraction médiane est que si $$\frac{a}{b}<\frac{c}{d}$$ et que $a$, $b$, $c$ et $d$ sont positifs, alors $$\frac{a}{b}<\frac{a+c}{b+d}<\frac{c}{d}$$

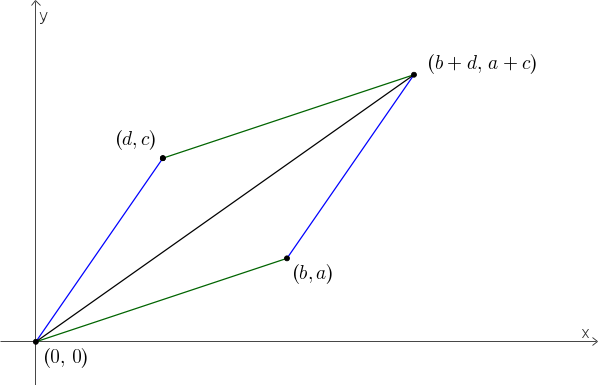
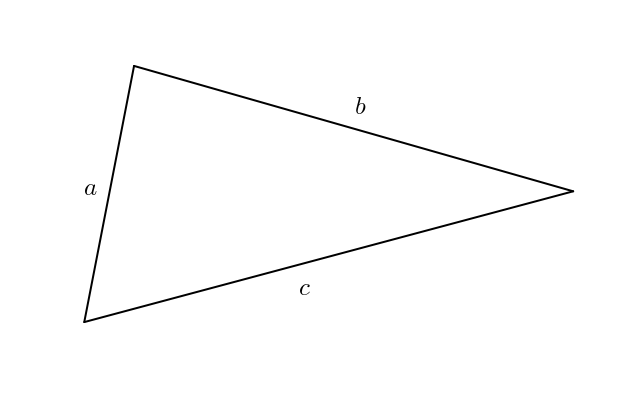
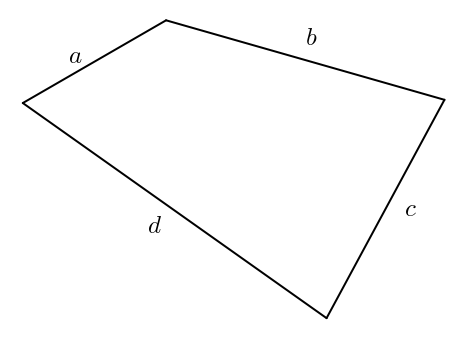
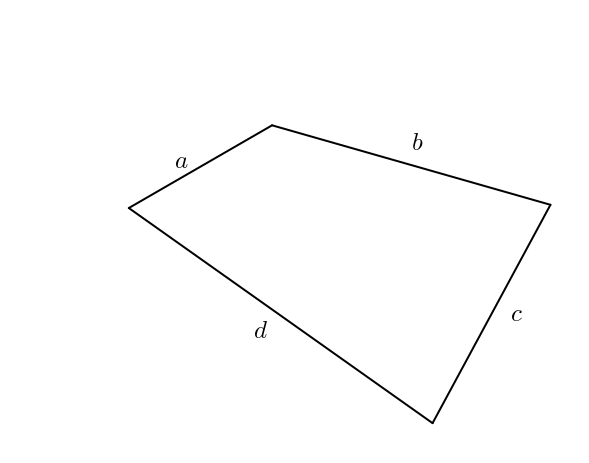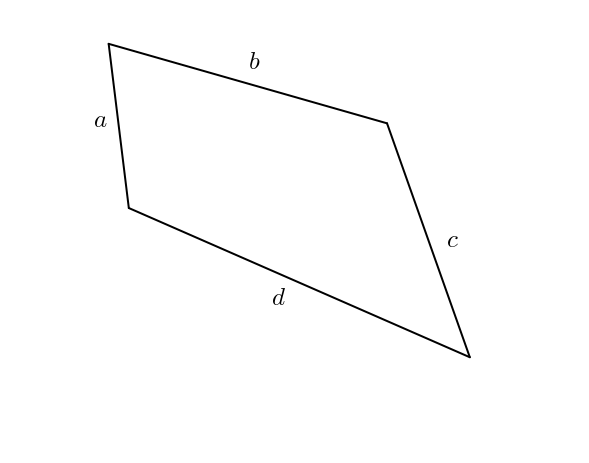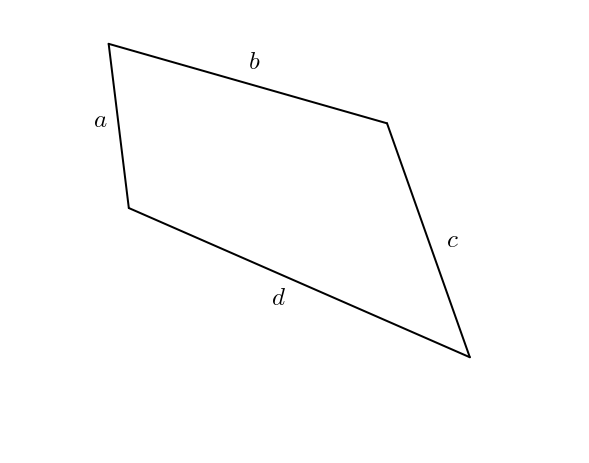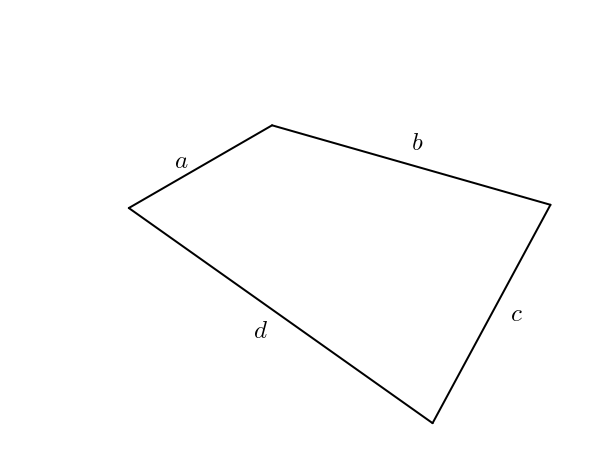
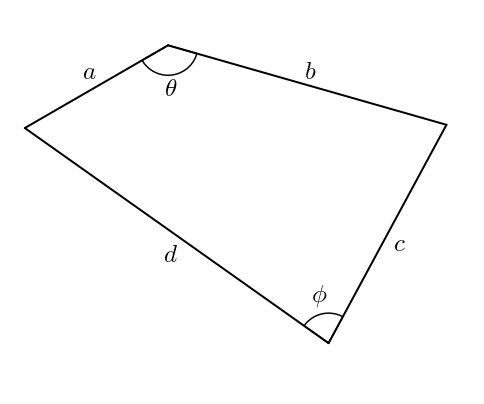
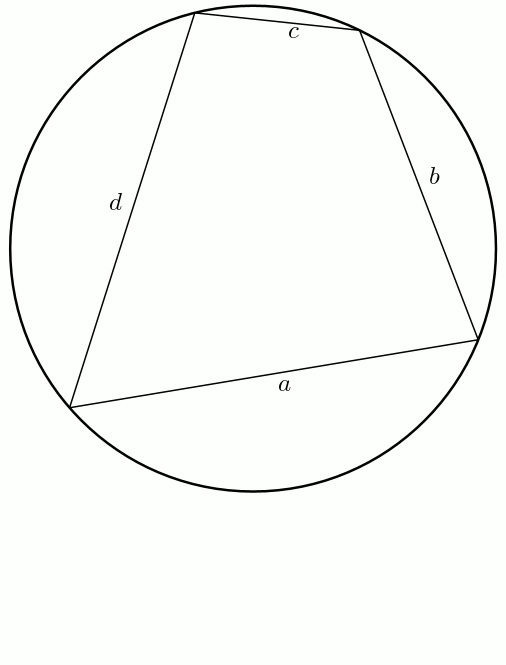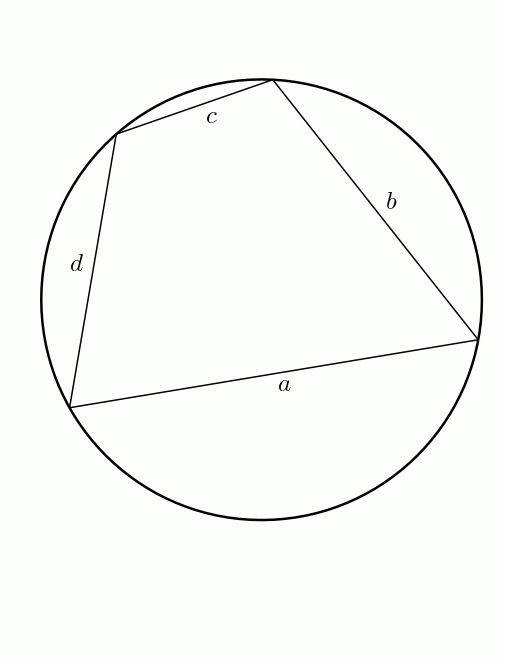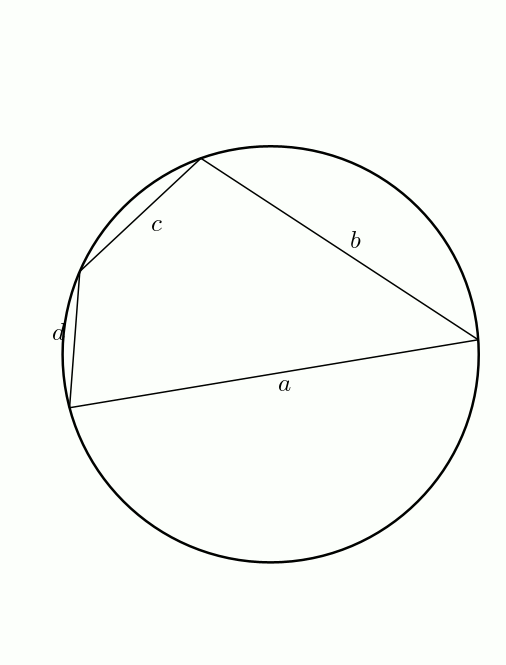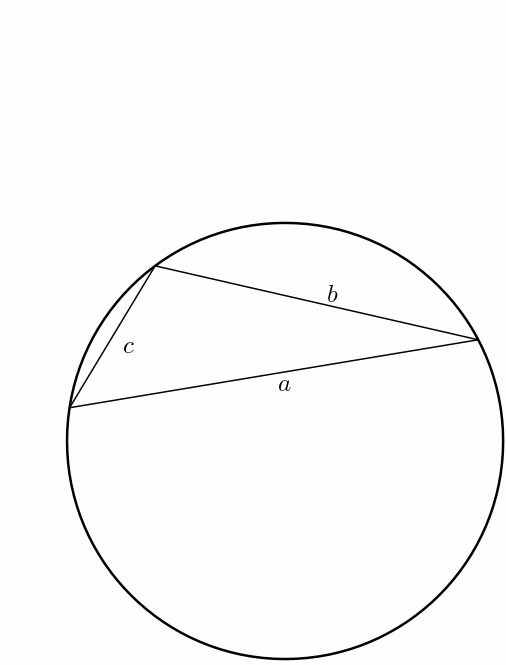
Les pentes des côtés du parallélogramme sont $\frac{a}{b}$ et $\frac{c}{d}$ et $\frac{a}{b}<\frac{c}{d}$.
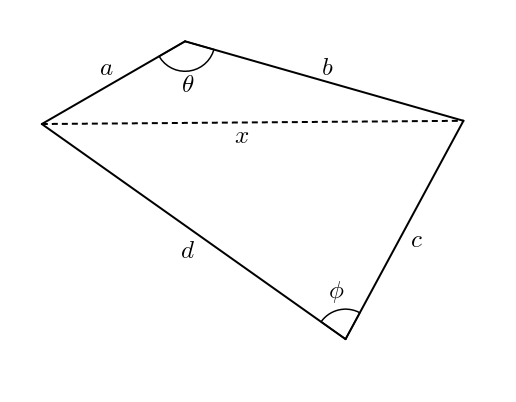
La pente de la diagonale du parallélogramme est $\frac{a+c}{b+d}$ et $\frac{a}{b}<\frac{a+c}{b+d}<\frac{c}{d}$.

On peut s’en convaincre algébriquement en calculant les différences strictement positives entre $\frac{a+c}{b+d}$ et $\frac{a}{b}$ $$\begin{array}{rl}\frac{a+c}{b+d}-\frac{a}{b}& =\frac{b(a+c)}{b(b+d)}-\frac{a(b+d)}{b(b+d)}\\ \\ & =\frac{ab+bc}{b^2+bd}-\frac{ab+ad}{b^2+bd}\\ \\ & =\frac{ab+bc-ab-ad}{b^2+bd}\\ \\ & =\frac{bc-ad}{b^2+bd}\\ \\ & =\frac{\frac{bc}{bd}-\frac{ad}{bd}}{\frac{b^2}{bd}+\frac{bd}{bd}}\\ \\ & =\frac{\frac{c}{d}-\frac{a}{b}}{\frac{b}{d}+1}>0\end{array}$$car $$\begin{array}{rl}\frac{c}{d}& >\frac{a}{b}\\ \\ \frac{c}{d}-\frac{a}{b}& >0\end{array}$$et $$\frac{b}{d}+1>0$$et entre $\frac{c}{d}$ et $\frac{a+c}{b+d}$ $$\begin{array}{rl}\frac{c}{d}-\frac{a+c}{b+d}& =\frac{c(b+d)}{d(b+d)}-\frac{d(a+c)}{d(b+d)}\\ \\ & =\frac{bc+cd}{bd+d^2}-\frac{ad+cd}{bd+d^2}\\ \\ & =\frac{bc+cd-ad-cd}{bd+d^2}\\ \\ & =\frac{bc-ad}{bd+d^2}\\ \\ & =\frac{\frac{bc}{bd}-\frac{ad}{bd}}{\frac{bd}{bd}+\frac{d^2}{bd}}\\ \\ & =\frac{\frac{c}{d}-\frac{a}{b}}{1+\frac{d}{b}}>0\end{array}$$ car $$\frac{c}{d}-\frac{a}{b}>0$$ et $$1+\frac{b}{d}>0$$Les fractions médianes peuvent donc nous servir à trouver des approximations rationnelles à des nombres irrationnels sans trop de peine. Par exemple, pour $\pi$, on peut utiliser les fractions $\frac{3}{1}$ et $\frac{4}{1}$ puisque $$\frac{3}{1}<\pi <\frac{4}{1}$$La première fraction médiane est $$\frac{3}{1}\oplus \frac{4}{1}=\frac{3+4}{1+1}=\frac{7}{2}$$Puisque $$\frac{3}{1}<\pi <\frac{7}{2}$$la deuxième fraction médiane serait $$\frac{3}{1}\oplus \frac{7}{2}=\frac{3+7}{1+3}=\frac{10}{3}$$Puisque $$\frac{3}{1}<\pi <\frac{10}{3}$$la suivante serait $$\frac{3}{1}\oplus \frac{10}{3}=\frac{10+3}{1+3}=\frac{13}{4}$$Puis comme $$\frac{3}{1}<\pi <\frac{13}{4}$$la suivante serait $$\frac{3}{1}\oplus \frac{13}{4}=\frac{3+13}{1+4}=\frac{16}{5}$$Puisque $\pi$ était beaucoup plus près de la fraction de départ $\frac{3}{1}$ que de la fraction de départ $\frac{4}{1}$, on semble s’approcher de $\pi$ par la droite, en d’autres mots, la fraction médiane est pour l’instant toujours supérieure à $\pi$. Bien sûr, cela ne sera pas toujours le cas. Poursuivons encore quelques étapes,$$\frac{3}{1}<\pi <\frac{16}{5}$$nous donne $$\frac{3}{1}\oplus \frac{16}{5}=\frac{3+16}{1+5}=\frac{19}{6}$$puis $$\frac{3}{1}<\pi <\frac{19}{6}$$nous donne $$\frac{3}{1}\oplus \frac{19}{6}=\frac{22}{7}$$approximation célébrée de $\pi$. $$\frac{3}{1}<\pi <\frac{22}{7}$$nous donne une enième approximation par la droite $$\frac{3}{1}\oplus \frac{22}{7}=\frac{3+22}{1+7}=\frac{25}{8}$$avant que $$\frac{22}{7}<\pi <\frac{25}{8}$$nous donne une première approximation par la gauche $$\frac{22}{7}\oplus \frac{25}{8}=\frac{25+22}{7+8}=\frac{47}{15}$$Les approximations obtenues avec les fractions médianes sont sensibles au choix des fractions de départ et convergent lentement par rapport à d’autres méthodes. Les meilleures approximations rationnelles sont celles obtenues à l’aide des fractions continues, et en comparaison, celles des fractions médianes font pâle figure. Il nous a fallu de nombreuses étapes pour trouver $$\frac{47}{15}\approx 3,1333$$une approximation qui n’est pas, en soi, exceptionnelle.

En outre, dans la suite,

en considérant les divisions comme des fractions, on approche le nombre mystère en trouvant la fraction médiane des deux dernier termes. Or, sans plan clair et agacé par le fait qu’on utilise uniquement les deux dernières fractions et jamais celle qui précède les deux dernières, comme c’est arrivé dans mon exemple pour $\pi$, j’ai eu l’impression d’emprunter un cul-de-sac. Or, ce n’était pas en vain : à quelle notion pourrait-on faire référence lorsqu’on considère les sommes des deux derniers termes ?

La suite de Fibonacci (oui !)

En effet, si on considère la suite de Fibonacci, $$1,1,2,3,5,8,13,21,34,55,89,144,233,377,610\dots$$on peut observer que les diviseurs correspondent aux quintuple des termes de de la suite.$$5,5,10,15,25,40,65,105,170,275,445,720,,1165,1885,3050\dots$$Pour les dividendes, c’est moins évident, mais ce sont les sextuple des termes de la suite, avec un déphasage $$6,6,12,18,30,48,78,126,204,330,534,864,1398,2262,3660\dots$$Si $F_n$ représente le $n^{\text{e}}$ terme de la suite de Fibonacci, alors les termes de la suite de l’infolettre sont $${\displaystyle \frac{6F_{n+2}}{5F_n}}$$En se rappelant que $F_{n+2}=F_{n+1}+F_n$, o peut évaluer la limite $$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}\frac{6F_{n+2}}{5F_n}& =\frac{6}{5}\cdot \underset{n\to \mathrm{\infty }}{lim}\frac{F_{n+2}}{F_n}\\ \\ & =\frac{6}{5}\cdot \underset{n\to \mathrm{\infty }}{lim}\frac{F_{n+1}+F_n}{F_n}\\ \\ & =\frac{6}{5}(\underset{n\to \mathrm{\infty }}{lim}1+\frac{F_{n+1}}{F_n})\\ \\ & =\frac{6}{5}(1+\underset{n\to \mathrm{\infty }}{lim}\frac{F_{n+1}}{F_n})\\ \\ & =\frac{6}{5}(1+\phi )\end{array}$$car tel que vu précédemment sur ce blogue, le rapport des termes consécutifs de la suite tendent vers $\phi =\frac{1+\sqrt{5}}{2}$.  Sachant en plus que $$\begin{array}{rl}1+\phi & =1+\frac{1+\sqrt{5}}{2}\\ \\ & =\frac{3+\sqrt{5}}{2}\\ \\ & =\frac{6+2\sqrt{5}}{4}\\ \\ & =\frac{1+2\sqrt{5}+5}{4}\\ \\ & =\frac{(1+\sqrt{5}{)}^2}{2^2}\\ \\ & ={\left(\frac{1+\sqrt{5}}{2}\right)}^2\\ \\ & ={\phi }^2\end{array}$$il est possible d’écrire $$\frac{6}{5}(1+\phi )=\frac{6}{5}{\phi }^2$$La suite tend donc vers $$\frac{6}{5}{\phi }^2=\frac{9+3\sqrt{5}}{5}\approx 3,141640786499873817845504201238$$un nombre qui est à moins de $0,000048132910080579383$ de $\pi$. Grâce à cette valeur, je suis ensuite tombé sur cette page chez Futility Closet, contenant la même référence au Journal of Recreational Mathematics, mais hélas sans plus de détails.

 

PS. Au moment où j’allais publier le billet, j’ai découvert une version de l’Inverseur disponible ici : http://wayback.cecm.sfu.ca/projects/ISC/ISCmain.html

J’avais foi en l’Inverseur et j’aurai eu raison ! En effet, on y trouve :
$$18+6\sqrt{5}\approx 31,41640786499873817$$ce qui nous aurait bien sûr mis sur la bonne piste.

 

Dans un triangle, la formule de Héron nous permet de calculer l’aire du triangle avec les mesures de ses côtés. Si $K$ est l’aire du triangle dont les côtés mesurent $a$, $b$ et $c$, alors $$K=\sqrt{s(s-a)(s-b)(s-c)}$$dans laquelle $s$ est le demi-périmètre $$s=\frac{a+b+c}{2}$$Nous avons rencontré la formule de Héron ici et ici. Existe-t-il une telle formule pour quadrilatère ? En d’autres mots, connaissant les mesures des quatre côtés d’un quadrilatère, est-il possible de déterminer son aire et de l’exprimer à l’aide d’une formule ?

Hélas, non, ce n’est pas possible. À partir d’un quadrilatère ayant pour côtés $a$, $b$, $c$ et $d$ comme côtés, il est possible de former une infinité de quadrilatères avec les mêmes mesures de côtés. Il suffit d’imaginer des charnières aux sommets du quadrilatère. On obtient un quadrilatère articulé.

Bon. Si ce petit billet se terminait ici, cela serait un peu ordinaire. Est-il possible de trouver quelque chose d’intéressant quand même concernant le quadrilatère, ses côtés et son aire ? Bien sûr ! Il faut cependant fixer, par exemple, les diagonales ou certains angles. Supposons que l’angle entre $a$ et $b$ soit $\theta$ et que l’angle entre $c$ et $d$ soit $\varphi$.

Les « charnières » ne sont plus libres de bouger. Le quadrilatère est fixe. Plus précisément, si on trace la diagonale $x$ comme dans la figure ci-dessous, on obtient deux triangles.

Il n’est pas très difficile ni très spectaculaire d’obtenir une expression pour l’aire du quadrilatère. Il suffit de faire la somme des aires des deux triangles. La formule d’aire trigonométrique du triangle nous donne l’expression recherchée instantanément.

$$K=\frac{ab\sin (\theta )}{2}+\frac{cd\sin (\varphi )}{2}$$

Cela reste tout de même un peu décevant et c’est pourquoi, chers lecteurs, je vous invite à suivre ces quelques étapes algébriques et trigonométriques supplémentaires.

La formule de Bretschneider

$$K=\frac{ab\sin (\theta )}{2}+\frac{cd\sin (\varphi )}{2}$$

On double,

$$2K=ab\sin (\theta )+cd\sin (\varphi )$$

et on élève au carré, $$4K^2=a^2{b}^2{\sin }^2(\theta )+2abcd\sin (\theta )\sin (\varphi )+c^2{d}^2{\sin }^2(\varphi )$$

et on quadruple

$$16K^2=4(a^2{b}^2{\sin }^2(\theta )+2abcd\sin (\theta )\sin (\varphi )+c^2{d}^2{\sin }^2(\varphi ))$$

D’autre part, en utilisant la loi des cosinus deux fois, une fois dans chaque triangle,

$$x^2=a^2+b^2-2ab\cos (\theta )$$ et $$x^2=c^2+d^2-2cd\cos (\varphi )$$

on obtient $$a^2+b^2-2ab\cos (\theta )=c^2+d^2-2cd\cos (\varphi )$$

On peut réarranger les termes pour obtenir $$\begin{array}{rl}{a}^2+b^2-c^2-d^2& =2ab\cos (\theta )-2cd\cos (\varphi )\\ \\ a^2+b^2-c^2-d^2& =2(ab\cos (\theta )-cd\cos (\varphi ))\end{array}$$

En élevant au carré et en regroupant les termes du même côté de l’égalité, on obtient

$$\begin{array}{rl}{(a^2+b^2-c^2-d^2)}^2& ={\left(2(ab\cos (\theta )-cd\cos (\varphi ))\right)}^2\\ \\ {(a^2+b^2-c^2-d^2)}^2& =4{(ab\cos (\theta )-cd\cos (\varphi ))}^2\\ \\ 0& =4{(ab\cos (\theta )-cd\cos (\varphi ))}^2-{(a^2+b^2-c^2-d^2)}^2\\ \\ & =4(a^2{b}^2{\cos }^2(\theta )-2abcd\cos (\theta )\cos (\varphi )+c^2{d}^2{\cos }^2(\varphi ))-{(a^2+b^2-c^2-d^2)}^2\end{array}$$

Il est ensuite possible d’additionner ces deux équations. On obtient

$$\begin{array}{rl}16K^2& =4(a^2{b}^2{\sin }^2(\theta )+2abcd\sin (\theta )\sin (\varphi )+c^2{d}^2{\sin }^2(\varphi ))\\ & \phantom{=}+4(a^2{b}^2{\cos }^2(\theta )-2abcd\cos (\theta )\cos (\varphi )+c^2{d}^2{\cos }^2(\varphi ))-{(a^2+b^2-c^2-d^2)}^2\\ \\ & =4(a^2{b}^2{\sin }^2(\theta )+2abcd\sin (\theta )\sin (\varphi )+c^2{d}^2{\sin }^2(\varphi )+a^2{b}^2{\cos }^2(\theta )\\ & \phantom{=}-2abcd\cos (\theta )\cos (\varphi )+c^2{d}^2{\cos }^2(\varphi ))-{(a^2+b^2-c^2-d^2)}^2\\ \\ & =4(a^2{b}^2({\sin }^2(\theta )+{\cos }^2(\theta ))+c^2{d}^2({\sin }^2(\varphi )+{\cos }^2(\varphi ))\\ & \phantom{=}-2abcd(\cos (\theta )\cos (\varphi )-\sin (\theta )\sin (\varphi ))-{(a^2+b^2-c^2-d^2)}^2\\ \\ & =4(a^2{b}^2+c^2{d}^2-2abcd\cos (\theta +\varphi ))-{(a^2+b^2-c^2-d^2)}^2\\ \\ & =4(a^2{b}^2+c^2{d}^2)-8abcd\cos (\theta +\varphi )-{(a^2+b^2-c^2-d^2)}^2\end{array}$$en utilisant, à l’avant-dernière étape $${\sin }^2(x)+{\cos }^2(x)=1$$et $$\cos (x+y)=\cos (x)\cos (y)-\sin (x)\sin (y)$$On note au passage que le choix de $\theta$ et $\varphi$ comme étant les angles entre $a$ et $b$ et entre $c$ et $d$ plutôt que les angles entre $a$ et $d$ et $b$ et $c$ n’a pas d’importance. Puisque la somme des mesures des angles intérieurs d’un quadrilatère est ${360}^{\circ }$, si les angles entre les côtés $a$ et $d$ et $b$ et $c$ sont respectivement $\alpha$ et $\beta$, on a $$(\theta +\varphi )+(\alpha +\beta )={360}^{\circ }$$ ce qui implique $$\cos (\theta +\varphi )=\cos (\alpha +\beta )$$Cela étant dit, à $$16K^2=4(a^2{b}^2+c^2{d}^2)-8abcd\cos (\theta +\varphi )-{(a^2+b^2-c^2-d^2)}^2$$on ajoute et retranche ensuite $8abcd$ à droite et on factorise le trinôme carré parfait. On obtient $$\begin{array}{rl}16K^2& =4(a^2{b}^2+c^2{d}^2)+8abcd-8abcd-8abcd\cos (\theta +\varphi )-{(a^2+b^2-c^2-d^2)}^2\\ \\ & =4(a^2{b}^2+2abcd+c^2{d}^2)-8abcd(1+\cos (\theta +\varphi ))-{(a^2+b^2-c^2-d^2)}^2\\ \\ & =4{(ab+cd)}^2-8abcd(1+\cos (\theta +\varphi ))-{(a^2+b^2-c^2-d^2)}^2\end{array}$$Sachant que $$\begin{array}{rl}1+\cos (x)& =1+\cos (\frac{x}{2}+\frac{x}{2})\\ \\ & =1+\cos \left(\frac{x}{2}\right)\cos \left(\frac{x}{2}\right)-\sin \left(\frac{x}{2}\right)\sin \left(\frac{x}{2}\right)\\ \\ & =1+{\cos }^2\left(\frac{x}{2}\right)-{\sin }^2\left(\frac{x}{2}\right)\\ \\ & =1+{\cos }^2\left(\frac{x}{2}\right)-(1-{\cos }^2\left(\frac{x}{2}\right))\\ \\ & =2{\cos }^2\left(\frac{x}{2}\right)\end{array}$$on peut poser $x=\theta +\varphi$ et l’équation devient $$\begin{array}{rl}16K^2& =4{(ab+cd)}^2-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)-{(a^2+b^2-c^2-d^2)}^2\\ \\ & =4{(ab+cd)}^2-{(a^2+b^2-c^2-d^2)}^2-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\end{array}$$Suivent quelques étapes algébriques élémentaires dans lesquelles on factorise des différences de carrés et des trinômes carrés parfaits.$$\begin{array}{rl}16K^2& =4{(ab+cd)}^2-{(a^2+b^2-c^2-d^2)}^2-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\\ \\ & ={(2ab+2cd)}^2-{(a^2+b^2-c^2-d^2)}^2-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\\ \\ & =(2ab+2cd-(a^2+b^2-c^2-d^2))(2ab+2cd+(a^2+b^2-c^2-d^2))-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\\ \\ & =(c^2+2cd+d^2-(a^2-2ab+b^2))(a^2+2ab+b^2-(c^2-2cd+d^2))-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\\ \\ & =({(c+d)}^2-{(a-b)}^2)({(a+b)}^2-{(c-d)}^2)-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\\ \\ & =(c+d-(a-b))(c+d+(a-b))(a+b-(c-d))(a+b+(c-d))-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\\ \\ & =(b+c+d-a)(a+c+d-b)(a+b+d-c)(a+b+c-d)-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\end{array}$$

Il ne reste que quelques étapes simples. On introduit le demi périmètre $s$ : $$s=\frac{a+b+c+d}{2}$$On obtient enfin $$\begin{array}{rl}16K^2& =(b+c+d-a)(a+c+d-b)(a+b+d-c)(a+b+c-d)-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\\ \\ & =(2)\left(\frac{b+c+d-a}{2}\right)(2)\left(\frac{a+c+d-b}{2}\right)(2)\left(\frac{a+b+d-c}{2}\right)(2)\left(\frac{a+b+c-d}{2}\right)-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\\ \\ & =16(\frac{a+b+c+d}{2}-\frac{2a}{2})(\frac{a+b+c+d}{2}-\frac{2b}{2})(\frac{a+b+c+d}{2}-\frac{2c}{2})(\frac{a+b+c+d}{2}-\frac{2d}{2})-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\\ \\ & =16(s-a)(s-b)(s-c)(s-d)-16abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)\end{array}$$En divisant par $16$ et en retenant la racine positive, on obtient $$K=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)}$$La formule de Bretschneider. Voilà !

Formule de Brahmagupta

En bonus ! La formule de Bretschneider se simplifie dans le cas d’un quadrilatère inscriptible (voir la toute fin de ce billet). En effet, dans un tel quadrilatère, les angles opposés sont supplémentaires. On a $\theta +\varphi ={180}^{\circ }$ ce qui fait $$\begin{array}{rl}{\cos }^2\left(\frac{\theta +\varphi }{2}\right)& ={\cos }^2\left(\frac{{180}^{\circ }}{2}\right)\\ \\ & ={\cos }^2\left({90}^{\circ }\right)\\ \\ & =0\end{array}$$et $$K=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd{\cos }^2\left(\frac{\theta +\varphi }{2}\right)}$$devient $$K=\sqrt{(s-a)(s-b)(s-c)(s-d)}$$toujours avec $$s=\frac{a+b+c+d}{2}$$

Formule de Héron

En bonus (bis) ! On peut obtenir facilement la formule de Héron à partir de celle de Brahmagupta. En effet, à partir d’un quadrilatère inscriptible, on fait tendre $d$ vers $0$. Le demi-périmètre $$s=\frac{a+b+c+d}{2}$$ tend vers $$s=\frac{a+b+c}{2}$$ et l’aire du quadrilatère $$K=\sqrt{(s-a)(s-b)(s-c)(s-d)}$$tend bien sûr vers $$K=\sqrt{s(s-a)(s-b)(s-c)}$$Voilà !

 

Références :

Niven, Ivan, Maxima and Minima Without Calculus, MAA, 1981

Alsina, Claudia and Roger B. Nelsen, A Cornucopia of Quadrilaterals, AMS/MAA Press, 2020

Johnson, Roger A, Advanced Euclidean Geometry, Dover, 2007

Le baseball est certainement le sport par excellence du point de vue de la statistique.  Aujourd’hui dans ce billet on s’intéresse plutôt à une autre facette, disons, géométrique de ce sport. Sur la page principale du site de la ligue majeure de baseball (MLB.com), on trouve le livre des règlements officiels (tout en bas de la page, sinon en suivant ce lien).

La section 2.02 et l’Annexe 2 décrivent le marbre (home base ou home plate) et nous indiquent les dimensions qu’il doit posséder. Voici l’extrait en question :

Home Base
Home base shall be marked by a five-sided slab of whitened rubber. It shall be a 17-inch square with two of the corners removed so that one edge is 17 inches long, two adjacent sides are 8½ inches and the remaining two sides are 12 inches and set at an angle to make a point. It shall be set in the ground with the point at the intersection of the lines extending from home base to first base and to third base; with the 17-inch edge facing the pitcher’s plate, and the two 12-inch edges coinciding with the first and third base lines. […] (See drawing D in Appendix 2.)

Annexe 2

C’est du sérieux. On utilise un carré de caoutchouc blanc de 17 pouces de côté duquel on retire deux coins (two corners removed) de telle sorte qu’on obtienne un pentagone possédant un côté de 17 pouces, deux côtés de 8½ pouces adjacents au côté de 17 pouces et deux côtés de 12 pouces se rejoignant en un même point et formant un angle. Un coup d’œil à l’Annexe 2 et au règlement concernant la disposition des buts et du marbre sur le terrain nous permet de déduire que cet angle est un angle droit.

Le carré de 17 pouces et ses deux coins ôtés

En pratique, les instructions sont claires et simples, mais d’un point de vue mathématique cela cause problème. D’abord, si two corners removed suggère qu’on n’enlève que deux triangles rectangles isocèles, des triangles rectangles dont les cathètes mesurent 8½ pouces, alors c’est bien sûr inexact !$$\begin{array}{rl}\sqrt{{\left(8\frac{1}{2}\right)}^2+{\left(8\frac{1}{2}\right)}^2}& =\sqrt{{\left(\frac{17}{2}\right)}^2+{\left(\frac{17}{2}\right)}^2}\\ \\ & =\sqrt{2{\left(\frac{17}{2}\right)}^2}\\ \\ & =\frac{17\sqrt{2}}{2}\\ \\ & \approx 12,02\end{array}$$Cela produit des côtés dont la mesure est légèrement supérieure à 12 pouces. Oups ! On doit donc enlever un peu plus que deux triangles rectangles ; en d’autres mots, l’intersection des deux côtés de 12 pouces ne coïncide pas avec le côté du carré, elle est légèrement en retrait. Soit.

Supposons qu’on ait bien des côtés de 12 pouces, le règlement suggère alors qu’il existe un triangle rectangle isocèle dont les cathètes mesurent 12 pouces et l’hypoténuse 17 pouces. Hélas ! C’est encore bien sûr impossible. $$\begin{array}{rl}\sqrt{{12}^2+{12}^2}& =\sqrt{2\cdot {12}^2}\\ \\ & =12\sqrt{2}\\ \\ & \approx 16,97\end{array}$$Une valeur légèrement inférieure à 17 pouces. Si près mais si loin en même temps ! Un tel marbre ne peut exister. Scandale !

Un marbre pentagonal qui aurait des côtés de 8½, 17, 8½, 12 et 12 contiendrait un angle $\theta$ de $$\begin{array}{rl}{17}^2& ={12}^2+{12}^2-2(12)(12)\cos (\theta )\\ \\ 289& =144+144-288\cos (\theta )\\ \\ \cos (\theta )& =-\frac{1}{288}\\ \\ \theta & \approx 90,2^{\circ }\end{array}$$

 

Référence :

Office of the Commissioner of Baseball, OFFICIAL BASEBALL RULES, 2023 Edition

Alsina, Claudi et Roger B. Nelsen, A Panoply of Polygons, AMS|MAA Press, 2023