The Dude Minds…

Ce n’est pas tous les jours qu’on demande à des élèves de troisième secondaire, qui sont en train d’apprendre, non sans mal, à différencier les nombres rationnels des nombres irrationnels, de marcher dans les pas de Wantzel, Hermite et von Lindemann.

Extrait du cahier d’exercices Sommets, Troisième secondaire, Chenelière Éducation

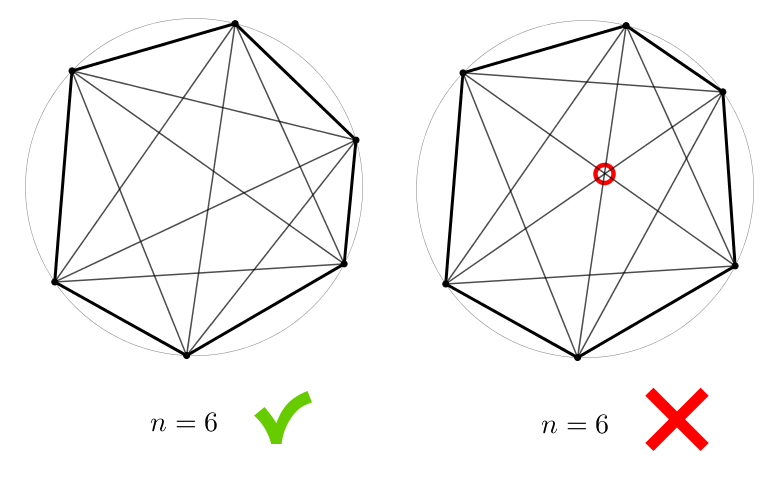
Démontre que la construction est irréalisable. Hmmmmm…. À quel genre de solution s’attend-on ici? Dans le cahier, nul mention des nombres constructibles (ce n’est pas au programme).

Ainsi est venu le temps d’un petit rappel à tous, qui pourtant semble relever de l’évidence : il faut faire les exercices (et les comprendre) et résoudre les problèmes avant de les donner aux élèves.

Aussi, je ne jetterai certainement pas la première pierre, car mon propre blogue regorge assurément de dizaines de coquilles, sinon erreurs, imprécisions ou détours inutiles, mais au prix qu’on paie chaque année pour ces cahiers, ça me déprime. Je dois avouer que je regrette un peu le temps révolu des manuels.

Et que disait le corrigé ? 

Bon ! Je pense qu’on peut passer au problème suivant !

Inspiré de cette question.

On place \(n\) points sur la circonférence d’un cercle pour former un polygone à \(n\) côtés tout en s’assurant qu’il n’y ait pas trois de ses diagonales ou plus qui se coupent en un même point.

Un classique

Combien y a-t-il de diagonales dans un tel polygone à \(n\) côtés ?

Une diagonale relie deux sommets qui ne sont pas adjacents. Pour tracer toutes les diagonales du polygone, on relie chaque sommet à tous les autres sommets, sauf trois : on ne peut relier un sommet à lui-même et aux deux sommets qui lui sont adjacents (en fait le sommet est déjà relié aux deux sommets qui lui sont adjacents par deux des côtés du polygone). Puisqu’il y a \(n\) sommets et que chaque sommet est relié à \(n-3\) autres sommets, on pourrait croire qu’il y a \(n(n-3)\) diagonales mais on ferait erreur. Chaque diagonale a deux extrémités, elle relie deux sommets. L’expression \(n(n-3)\) compte donc les diagonales en double. On a plutôt \[\text{nombre de diagonales} = \frac{n(n-3)}{2}\]Génial non ? 

Dans le polygone ci-dessus à \(9\) côtés, inutile de compter les diagonales une par une : il y en a \[\frac{9(9-3)}{2} = \frac{9\cdot 6}{2} = 27\]

La suite

Combien y a-t-il de points d’intersection formés par les diagonales ?

Hmmm… là, ça semble moins évident. Combien de points d’intersection ces diagonales forment-elles en effet ? Lorsque j’ai donné ce problème à un collègue, il s’est empressé de faire ce que tout bon matheux fait : étudier d’abord les petits cas, consigner les données et y chercher une régularité.

Nombre de côtés \(n\)	Nombre de points d'intersection formés par les diagonales
4	1
5	5
6	15
7	35
8	70
9	126
...	...

Je dois avouer que pour ma part, ces nombres ne me disaient pas grand chose. Une petite analyse des accroissements semble éventuellement révéler un polynôme de degré 4 [1].

Mais en tant que fin amateur du triangle de Pascal, mon collègue a tout de suite remarqué ceci : 

 

Comment cela pourrait-il nous aider à découvrir la solution ? En comptant à partir du 0^e étage du triangle, l’allée verte apparaît pour la première fois seulement au quatrième étage. Ce n’est peut-être pas si surprenant sachant que les triangles n’ont pas de diagonales et qu’on ne peut considérer des polygones à \(0\), \(1\) ou \(2\) côtés. Considérant ensuite que les entrées du triangle correspondent aux coefficients binomiaux, le premier \(1\) vert peut être interprété comme le nombre de façons de choisir sans répétition et sans ordre \(4\) éléments dans un ensemble de \(4\) éléments. Le \(5\) vert qui suit, au cinquième étage, correspond au nombre de façons de choisir sans répétition et sans ordre \(4\) éléments dans un ensemble de \(5\) éléments. Le \(15\) vert qui suit correspond au nombre de façon de choisir sans répétition et sans ordre \(4\) éléments dans un ensemble de \(6\) éléments. Et ainsi de suite… Comment tout cela se traduit-il géométriquement ? 

Si on choisit quatre sommets parmi les \(n\) sommets du polygone, on forme un quadrilatère. Ce quadrilatère possède deux diagonales qui se coupent ! Bien sûr, les diagonales du quadrilatère appartiennent aussi au polygone à \(n\) côtés. Et chaque couple de diagonales du polygone à \(n\) côtés, qui définissent chaque point d’intersection, appartient à un quadrilatère unique. Ainsi, le nombre de points d’intersection des diagonales correspond au nombre de quadrilatères qu’il est possible de former avec les \(n\) sommets. En d’autres mots, c’est le nombre de façons de choisir sans répétition et sans ordre \(4\) sommets dans un ensemble de \(n\) sommets. \begin{align*}\text{nombre de points d’intersection} &= \binom{n}{4}\\ \\  &= \frac{n!}{4!(n-4)!}\end{align*}

 

[1]  Pour les curieux, le polynôme en question est \[\frac{1}{24}\left(n^{4}-6n^{3}+11n^{2}-6n\right)\]

On a déjà vu la méthode « classique » au début de ce billet, ici. Là, on s’intéresse à la version combinatoire.

On considère l’ensemble \[\left\{0, \, 1, \, 2,\, 3,\ \dots \ , \, n \right\}\]De combien de façons peut-on choisir deux nombres de cet ensemble qui contient \(n+1\) éléments ?

D’une part, si on se rappelle nos combinaisons, il y a \begin{align*}\binom{n+1}{2} &= \frac{(n+1)!}{2!(n+1-2)!} \\ \\ &=\frac{(n+1)(n)(n-1)!}{(2)(1)(n-1)!}\\ \\ &=\frac{n(n+1)}{2}\end{align*}façons de choisir deux nombres de cet ensemble qui contient \(n+1\) éléments.

D’autre part, si on choisit deux nombres dans \(\left\{0, \, 1, \, 2,\, 3,\, \dots, \, n \right\}\), il y aura forcément un nombre plus grand que l’autre. Puisque \(0\) ne peut être le plus grand nombre, celui-ci sera choisi dans l’ensemble \(\left\{1, \, 2, \, 3, \ \dots  \ , \, n\right\}\) qui comporte \(n\) éléments. Disons que ce nombre est \(k\). Le plus petit nombre peut donc être choisi dans l’ensemble suivant \[\left\{0,\, 1,\, 2,\, 3, \ \dots \ , \, k-1\right\}\]qui comporte \(k\) éléments. En d’autres mots, pour chacune des possibilités pour le plus grand nombre, il y a \(k\) possibilités pour le plus petit nombre. Ainsi, le nombre de sélections possibles est donc \[\sum_{k=1}^{n}k=1 + 2 + 3 + \ \dots \ + n\]

Puisqu’on a compté la même chose de deux manières différentes, on a \[\sum_{k=1}^{n} k = \frac{n(n+1)}{2}\]

Référence : Benjamin, Arthur T. et Jennifer J. Quinn, Proofs that Really Count : The Art of Combinatorial Proof, MAA Press, 2003