Bien embêté est celui qui veut convaincre un jeune de troisième secondaire que le volume d’une pyramide est égal au tiers du volume du prisme de même base et de même hauteur, sans recourir à quelconque artifice des mathématiques supérieures. Quand je demande aux élèves « pourquoi est-ce ainsi ? », ils me répondent unanimement qu’ils ont vu leur enseignant, armé de ces solides creux de plastique et d’un verre d’eau, remplir le prisme d’eau avec le contenu de trois pyramides. Voilà ! Ça rentre trois fois ! Ils sont convaincus. Comment leur faire part, alors, que la réalisation de cette expérience est possible parce que le volume de la pyramide de même base et de même hauteur est le tiers de celui du prisme et non l’inverse ! Distinction importante, confusion inévitable.
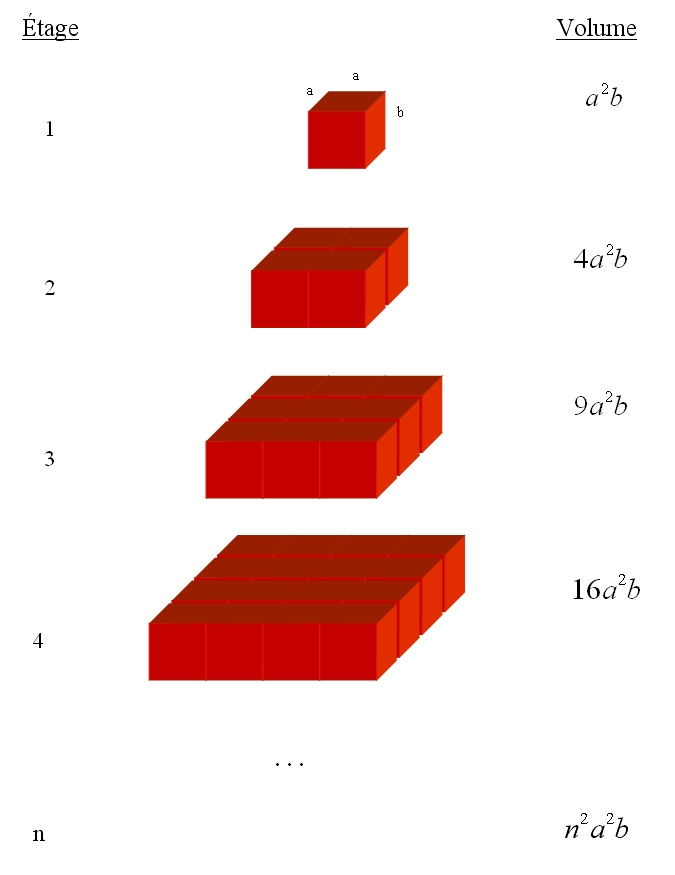
Bon voici. On a seulement besoin d’un petit résultat préliminaire, déjà examiné dans ce billet : la somme des \(n\) premiers carrés. La sommes des \(n\) premiers carrés est : \[\frac{n(n+1)(2n+1)}{6}\]Commençons. Nous allons construire une pyramide un peu approximative, un peu grossière, comme si elle était faite de blocs. Le premier étage est composé d’un seul bloc, dont on fixera, pour les besoins de la cause, les dimensions à \(a\times a\times b\). Le deuxième étage est composé de quatre blocs isométriques. Le troisième étage de neuf de ces blocs isométriques. Et ainsi de suite…
Notre « pyramide » possède \(n\) étages comme dans le schéma suivant
La volume de la « pyramide » sera donc égal à la somme des volumes des étages. On obtient \[V_{p} = a^{2}b+4a^{2}b+9a^{2}b+\dots +n^{2}a^{2}b\]En mettant \(a^{2}b\) en évidence, on obtient \[V_{p}=a^{2}b\left(1+4+9+\dots+n^{2}\right)\]On reconnait immédiatement la somme des \(n\) premiers carrés dans la parenthèse. On peut donc réécrire la dernière formule comme \[V_{p}=a^{2}b\left(\frac{n(n+1)(2n+1)}{6}\right)\]que l’on développe pour obtenir \[V_{p}=a^{2}b\left(\frac{2n^{3}+3n^{2}+n}{6}\right)\]Pour des raisons encore obscures, mais qui deviendront rapidement apparentes, on décide me mettre en évidence le cube de \(n\) dans la parenthèse \[V_{p}=a^{2}b\cdot n^{3}\left(2+\frac{3}{n}+\frac{1}{n^{2}}\right)\left(\frac{1}{6}\right)\]On trouve d’abord que la hauteur de la « pyramide » est égale à \(n\) fois (il y a, après tout, \(n\) étages) la hauteur \(b\) du prisme à base carré. Si \(h\) est la hauteur de la « pyramide », alors on a \[h=bn\]On trouve ensuite une expression pour l’aire de la base de la « pyramide ». En effet, au énième et ultime étage, il y a \(n^{2}\) petits carrés d’aire \(a^{2}\) . Si \(A_{b}\) est l’aire de la base de la « pyramide », alors on a \[A_{b} = a^{2}n^{2}\]Le besoin de mettre le cube de \(n\) en évidence est maintenant clair, on peut réécrire \[V_{p} = a^{2}b \cdot n^{3}\left(2+\frac{3}{n}+\frac{1}{n^{2}}\right)\left(\frac{1}{6}\right)\]comme \[V_{p}=\left(a^{2}n^{2}\right)\left(bn\right)\left(2+\frac{3}{n}+\frac{1}{n^{2}}\right)\left(\frac{1}{6}\right)\]ce qui est équivalent à \[V_{p}= A_{b}\cdot h\left(2+\frac{3}{n}+\frac{1}{n^{2}}\right)\left(\frac{1}{6}\right)\]La clé du raisonnement est ici. En fixant l’aire de la base et la hauteur, et mais en augmentant le nombre d’étages \(n\), on obtient un solide qui s’apparente de plus en plus à la pyramide recherchée. Si \(n\) augmente, alors \(a^{2}\) (et donc \(a\)) diminue dans \[A_{b} = a^{2}n^{2}\]En d’autres mots, le sommet de la “pyramide” devient de plus en plus pointu. Si bien qu’en faisant tendre \(n\) vers l’infini, \(a^{2}\) (et donc aussi \(a\)) tend vers zéro. D’autre part, si \(n\) augmente, \(b\) diminue dans \[h=bn\]En d’autres mots, les faces de la « pyramide » deviennent de plus en plus « lisses » : les marches plus nombreuses, mais les contre-marches plus petites. Si bien qu’en faisant tendre \(n\) vers l’infini, \(b\) tend vers zéro. En faisant tendre \(n\) vers l’infini, on obtient notre pyramide ! Dans la formule, les termes \[\frac{1}{n} \quad \text{et} \quad \frac{1}{n^{2}}\]tendent alors tous les deux vers zéro lorsque \(n\) tend vers l’infini. On obtient donc \[V_{p} = A_{b}\cdot h\left(2+0+0\right)\left(\frac{1}{6}\right)\]ce qui fait\[V_{p}=\frac{A_{b}\cdot h}{3}\]La fameuse formule recherchée !