The Dude Minds…

Voici une méthode astucieuse pour produire des triplets pythagoriciens, c’est-à-dire des triplets de nombres entiers non-nuls qui satisfont la relation de Pythagore : $$a^2+b^2=c^2$$On choisit deux nombres entiers strictement positifs.  On appelle le plus grand de ces deux nombres $x$ et l’autre, le plus petit, $y$  .  On calcule $$a=2xy,b=x^2-y^2\text{et}c=x^2+y^2$$On obtient ainsi un triplet de nombres entiers qui satisfont la relation de Pythagore.  En effet, on observe que $$\begin{array}{rl}{a}^2+b^2& =(2xy{)}^2+{(x^2-y^2)}^2\\ \\ & =4x^2{y}^2+x^4-2x^2{y}^2+y^4\\ \\ & =x^4+2x^2{y}^2+y^4\\ \\ & ={(x^2+y^2)}^2\\ \\ & =c^2\end{array}$$

Voilà !

Prenez quelques minutes de votre temps et découvrez ce résultat fort étonnant.

Ce qu’il faut savoir :

Dans un triangle, les trois médiatrices sont concourantes ;

dans un triangle, les trois hauteurs sont concourantes ;

dans un triangle, les trois médianes sont concourantes.

Voilà ce qu’il faut savoir ! Eh bien commençons !  Tout point situé sur la médiatrice d’un segment est équidistant des deux extrémités du segment.  Traçons la médiatrice de $AB$ qui la coupe en $C$.  $D$ est un point de cette médiatrice.  Montrons que $$\overline{AD}\cong \overline{BD}$$Le cas est trivial si $D$ et $C$ sont confondus, point milieu de $\overline{AB}$ (définition de médiatrice).

Si $D$ n’est pas en $C$, alors par définition de médiatrice,  on a  bien $$\overline{AC}\cong \overline{BC}$$et on a aussi $$m\mathrm{\angle }ACD=m\mathrm{\angle }BCD={90}^{\circ }$$Puisque les triangles $ACD$ et $BCD$ partagent le côté $CD$,  on trouve qu’ils sont isométriques par le cas d’isométrie CAC.  Et comme dans les triangles isométriques les côtés homologues sont isométriques, on trouve $$\overline{AD}\cong \overline{BD}$$La réciproque est aussi vraie.  Si $D$ est équidistant de $A$ et de $B$, on peut affirmer que $$\overline{AD}\cong \overline{BD}$$En particulier, si $D$ était sur $\overline{AB}$ ($C$ sur l’image), on aurait aussi $$\overline{AC}\cong \overline{BC}$$Puisque les deux triangles $ACD$ et $BCD$ partagent le côté $CD$, on trouve qu’ils sont isométriques par CCC.  Les angles $ACD$ et $BCD$ étant d’une part des angles homologues isométriques, et d’autre part adjacents supplémentaires, on déduit que $$m\mathrm{\angle }ACD=m\mathrm{\angle }BCD={90}^{\circ }$$$DC$ est donc une médiatrice.

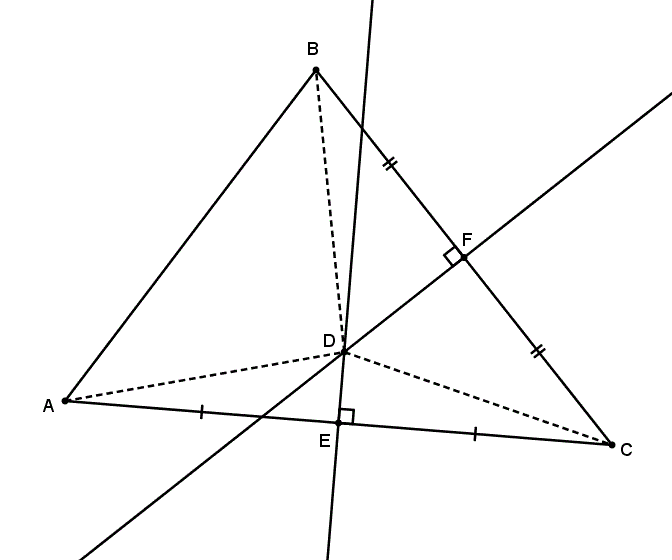
Considérons le triangle $ABC$ suivant.  $DF$ est la médiatrice de $\overline{BC}$ et $DE$ est la médiatrice de $\overline{AC}$.  Les deux médiatrices se coupent en $D$.

Puisque $DF$ est la médiatrice de $\overline{BC}$, on trouve $$\overline{BD}\cong \overline{CD}$$Puisque $DE$ est la médiatrice de $\overline{AC}$, on trouve $$\overline{AD}\cong \overline{CD}$$et par transitivité, on conclut que $$\overline{AD}\cong \overline{BD}$$Mais cela implique donc que $D$ est situé sur le médiatrice de $\overline{AB}$ puisqu’il est équidistant de $A$ et de $B$ ! Les trois médiatrices se rencontrent en un point.  C’était la première chose à savoir !

Portons maintenant notre attention sur le triangle $ABC$ suivant :

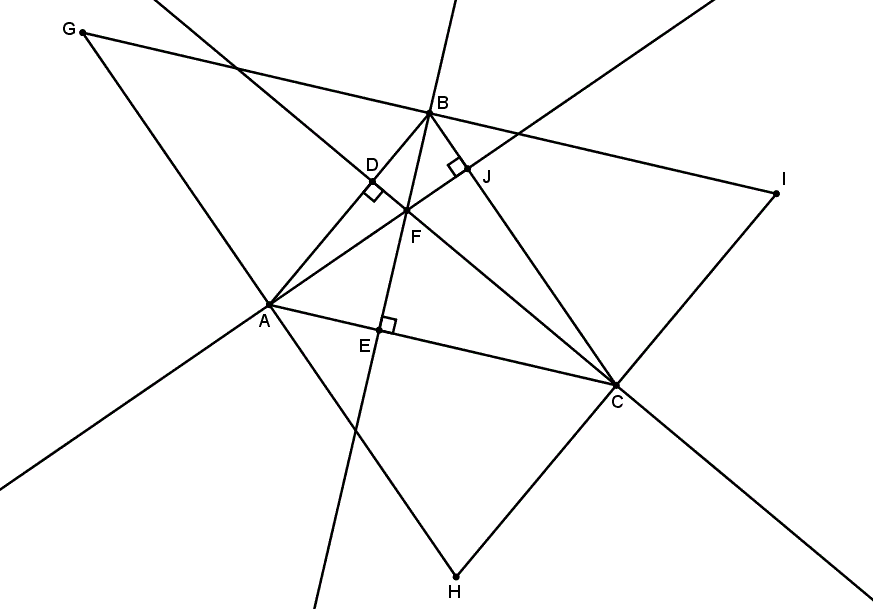
On a d’abord tracé les trois hauteurs $AJ$, $BE$ et $CD$.  On a ensuite tracé $GI$ parallèle à $AC$ et passant par $B$, $HI$ parallèle à $AB$ et passant par $C$ et $GH$ parallèle à $BC$ et passant par $A$.

Toutes ces droites parallèles forment évidemment une panoplie d’angles alternes-internes isométriques.

Considérons les parallèles $AC$ et $GI$ et la sécante $BC$.  Les angles $IBC$ et $ACB$ sont alternes-internes isométriques.

Considérons les parallèles $AB$ et $HI$ et la sécante $BC$.  Les angles $ABC$ et $BCI$ sont aussi alternes-internes isométriques.

Les triangles $BIC$ et $ABC$ partagent le côté $BC$ et sont donc isométriques par $ACA$.  Et comme dans les triangles triangles isométriques, les côtés homologues sont isométriques, on trouve$$\overline{AC}\cong \overline{BI}$$Considérons les parallèles $BC$ et $GH$ et la sécante $AB$.  Les angles $GAB$ et $ABC$ sont alternes-internes isométriques.

Considérons à nouveau les parallèles $AC$ et $GI$ et la sécante $AB$.   Les angles $GBA$ et $BAC$ sont alternes-internes isométriques.

Les triangles $GAB$ et $CBA$ partagent le côté $AB$ et sont donc isométriques par $ACA$.  Et comme dans les triangles triangles isométriques, les côtés homologues sont isométriques, on trouve$$\overline{AC}\cong \overline{BG}$$Cela implique donc, par transitivité, que $$\overline{BG}\cong \overline{BI}$$On peut dire que $B$ est le point milieu de $\overline{GI}$.  Par le même raisonnement, on pourrait trouver que $A$ est le point milieu de $\overline{GH}$ et $C$ est le point milieu de $\overline{HI}$.

Comme $BE$ est perpendiculaire à $AB$ (définition de hauteur) et $AB$ est parallèle à $GI$ (par construction), on a $BE$ perpendiculaire à $GI$.  Par le même raisonnement, on trouve que $AJ$ est perpendiculaire à $GH$ et $DC$ est perpendiculaire à $HI$.

$BE$, $AJ$ et $DC$ sont donc les médiatrices du triangle $GHI$.  Et comme les médiatrices sont concourantes, on trouve que $BE$, $AJ$ et $DC$, qui sont aussi les hauteurs de $ABC$, se rencontrent en $F$.  Les trois hauteurs d’un triangle se rencontrent donc en un même point.  C’était la deuxième chose à savoir !

Considérons maintenant le triangle $ABC$ suivant :

Dans le triangle $ABC$, on a tracé les médianes $CE$ et $AD$ qui se coupent en $G$.  Traçons aussi $DE$.  Par définition de médiane, on trouve que $$m\overline{AB}=2m\overline{BE}$$et $$m\overline{BC}=2m\overline{BD}$$Les triangles $ABC$ et $EBD$ partagent l’angle $EBD$.  Ils sont donc semblables par CAC.  Puisque dans les triangles semblables les côtés homologues sont dans le même rapport, on déduit que $$m\overline{AC}=2m\overline{ED}$$Dans les triangles semblables, les angles homologues étant isométriques, on trouve que les angles $BED$ et $BAC$ sont isométriques.  Et puisque ces angles sont aussi correspondants, on trouve que $ED$ est parallèle à $AC$ (puisque des angles correspondants isométriques sont formés par des parallèles).  En considérant cette dernière paire de parallèles et la sécante $CE$, on trouve que les angles $DEG$ et $ACG$ sont alternes-internes isométriques.  Avec les angles $EGD$ et $CGA$ opposés par le sommet, et donc isométriques, on conclut que les triangles $EGD$ et $CGA$ sont semblables par AA.  On avait déjà établit que $$m\overline{AC}=2m\overline{ED}$$et puisque dans les triangles semblables on observe des côtés homologues proportionnels, alors on déduit que $$m\overline{EG}=2m\overline{CG}$$et $$m\overline{DG}=2m\overline{AG}$$Les médianes se coupent donc au ${\displaystyle \frac{2}{3}}$ de leur longueur à partir du sommet (ou dans un rapport $2:1$).  En répétant cette démarche avec l’autre médiane, on trouve que les médianes se rencontrent effectivement en un même point.  C’était la troisième chose à savoir !

Enfin, considérons le triangle $ABC$ suivant :

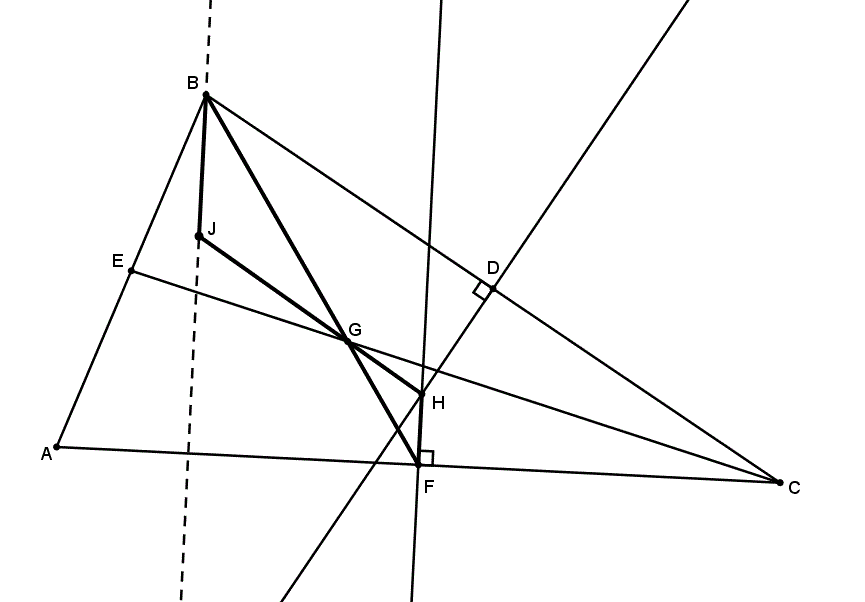
$BF$ et $CE$ sont deux droites supportant les médianes se coupant en $G$.  $FH$ et $DH$ sont deux médiatrices se coupant en $H$.  Prolongeons $GH$ jusqu’en $J$ de telle sort que $$m\overline{GJ}=2m\overline{GH}$$On sait que $$m\overline{GB}=2m\overline{GF}$$On trouve aussi que l’angle $JGB$ est congru à l’angle $HGF$ puisqu’ils sont opposés par le sommet.  Les triangles $JGB$ et $HGF$ sont donc semblables par le cas de similitude CAC.

Et comme dans les triangles semblables, les angles homologues sont isométriques, on trouve$$\mathrm{\angle }GJB\cong \mathrm{\angle }GHF$$Cela implique que les droites $JB$ et $FH$ sont parallèles puisque des angles alternes-internes isométriques sont formés par des parallèles (en utilisant la sécante $JH$).

Puisque $HF$ est une médiatrice, on trouve que $HF$ et $AC$ sont perpendiculaires.  $JB$ est donc aussi perpendiculaire à $AC$.  $JB$ est donc supportée par la hauteur issue de $B$.  $J$est donc le point d’intersection des hauteurs.

Dans un triangle, les points d’intersection des hauteurs, des médianes et des médiatrices sont alignées sur une même droite : la droite d’Euler.

Référence : Dörrie, Heinrich, 100 Great Problems of Mathematics (1965)