The Dude Minds…

On connait beaucoup de choses sur les médianes, les hauteurs, les médiatrices ou les bissectrices d’un triangle.  Le  théorème  de Stewart  concerne les segments internes du triangles joignant un sommet à son côté opposé d’une manière quelconque .  Considérons le triangle suivant :

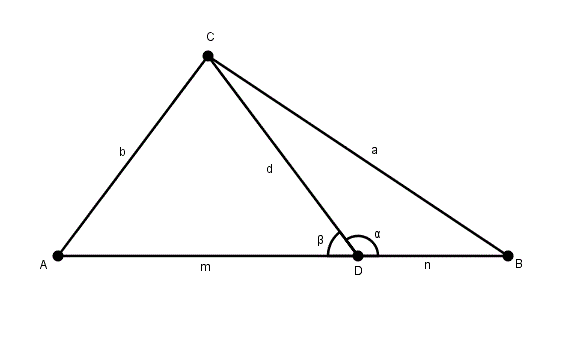
Remarquons que$$\alpha +\beta ={180}^{\circ }$$et donc que $$\cos (\alpha )=-\cos (\beta )(1)$$Avec la loi des cosinus, dans le triangle $ADC$, on trouve$$b^2=m^2+d^2–2md\cdot \cos (\beta )$$En isolant le cosinus, on obtient$$\cos (\beta )=\frac{-b^2+m^2+d^2}{2md}$$Avec la loi des cosinus, mais cette fois-ci dans le triangle $CDB$, on obtient$$a^2=n^2+d^2–2nd\cdot \cos (\alpha )$$En isolant le cosinus, on obtient$$\cos (\alpha )=\frac{-a^2+n^2+d^2}{2nd}$$Ce qui implique en vertu de $(1)$ que$$-\cos (\beta )=\frac{-a^2+n^2+d^2}{2nd}$$Et donc que$$\cos (\beta )=\frac{a^2–n^2–d^2}{2nd}$$En égalant les deux expressions, on obtient$$\frac{-b^2+m^2+d^2}{2md}=\frac{a^2–n^2–d^2}{2nd}$$Puis en mettant sur dénominateur commun$$\frac{-b^{2}n+m^{2}n+d^{2}n}{2mnd}=\frac{a^{2}m–n^{2}m–d^{2}m}{2mnd}$$ce qui fait$$-b^{2}n+m^{2}n+d^{2}n=a^{2}m–n^{2}m–d^{2}m$$ou de manière équivalente$$d^{2}n+d^{2}m+m^{2}n+n^{2}m=a^{2}m+b^{2}n$$En effectuant une mise en évidence double, on obtient$$d^2(n+m)+nm(m+n)=a^{2}m+b^{2}n$$puis$$(d^2+nm)(m+n)=a^{2}m+b^{2}n$$Et comme$$c=m+n$$on obtient finalement$$c(d^2+nm)=a^{2}m+b^{2}n$$Voilà ! Le théorème de Stewart.

Référence :  Alfred S. Posamentier et Salkind, Charles T., Challenging Problems In Geometry (1996)