Partage équitable

Saviez-vous que dans un triangle, il existe toujours au moins une droite qui partage le périmètre et l’aire en deux parties égales en même temps ?

L’aire

On considère un point $P$ dans un triangle $ABC$ quelconque. Soit une droite qui passe par $P$ et qui divise le triangle en deux régions. Sur le schéma ci-dessous, on a colorié les deux régions en rouge et en vert. On pose $K$ l’aire du triangle $ABC$. L’aire du triangle rouge est $rK$ et celle du quadrilatère vert est $(1-r)K$ avec, bien entendu, $0<r<1$. Si les deux régions, la rouge et la verte, ont la même aire, c’est-à-dire si $r=1-r=\frac{1}{2}$, alors on a gagné ! Cette droite fait l’affaire, inutile de cherche plus loin !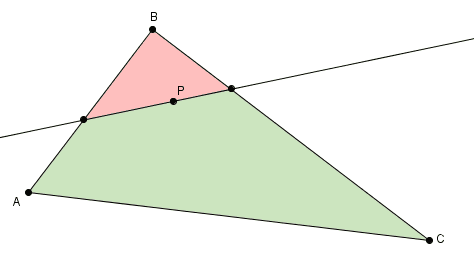

Si les deux régions n’ont pas la même aire, comme c’est fort probablement le cas, voici comment on procède [1]. On effectue la rotation (par exemple, antihoraire) de la droite, autour du point $P$. Lorsque la droite tourne autour du point $P$, les aires changent. Si l’aire de la région rouge change, passant de $rK$ à $r_{1}K$, celle de la verte change aussi, passant de 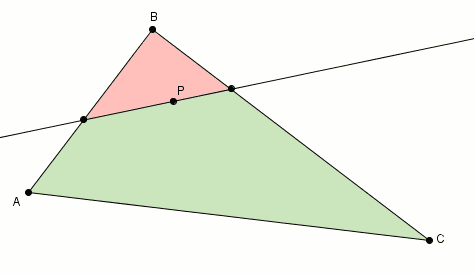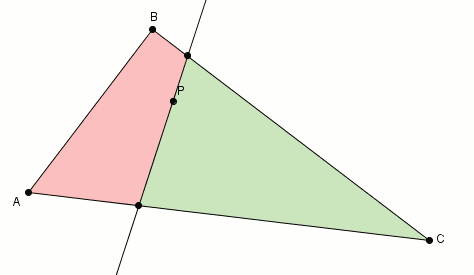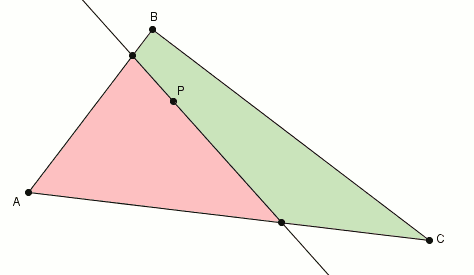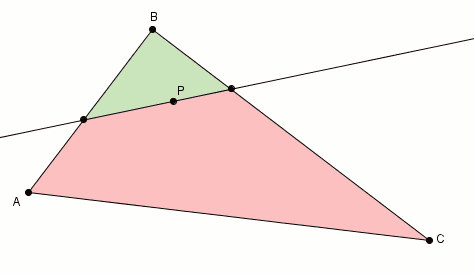$(1-r)K$ à $(1-r_1)K$.

Qu’arrive-t-il à la valeur de $r$ lorsque la droite effectue un demi-tour ? Les régions rouge et verte s’intervertissent leur rôle. La droite étant envoyée sur elle-même grâce à la rotation de 180° de centre $P$, la région rouge, initialement d’aire $rK$, devient la région d’aire $(1-r)K$, et vice-versa pour la région verte (initialement d’aire $(1-r)K$, elle devient la région d’aire $rK$). Si $r$ est au départ inférieur à $\frac{1}{2}$, alors $1-r$ est supérieur à $\frac{1}{2}$ et, réciproquement, si $r$ est au départ supérieur à $\frac{1}{2}$, alors $1-r$ est inférieur à $\frac{1}{2}$. En passant de manière continue de $r$ à $r-1$, la valeur intermédiaire de $\frac{1}{2}$ est certainement atteinte.

Le périmètre

Un raisonnement semblable peut être appliqué pour trouver une droite qui divise le périmètre en deux parties de même longueur.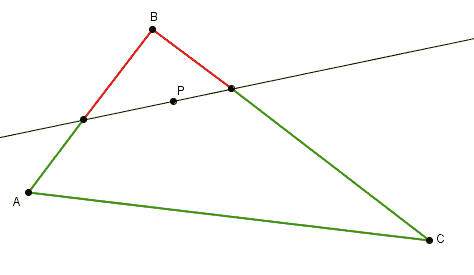

En effectuant la rotation de la droite autour du point $P$, les segments rouges et verts s’intervertissent leur rôle.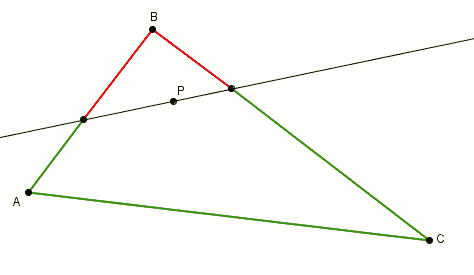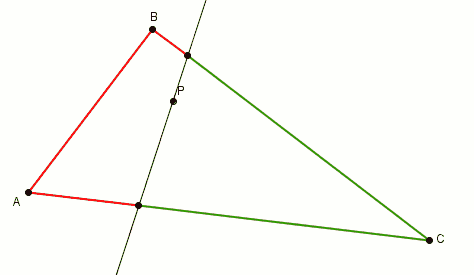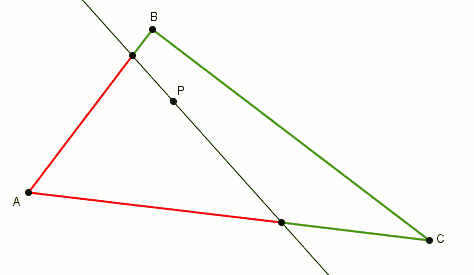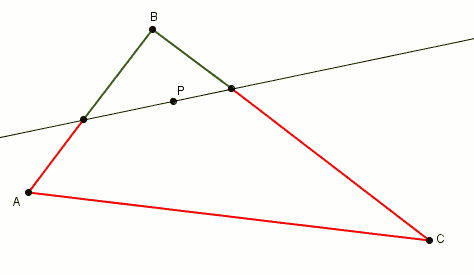

Il est donc possible de trouver une droite qui divise le périmètre en deux parties de même longueur pour une certaine position intermédiaire. On note cependant qu’il ne s’agit pas, en général, de la même droite qui divise aussi l’aire en deux régions de même aire. On note aussi au passage que cet argument peut s’appliquer à n’importe quel polygone convexe, pas seulement au triangle !

L’aire et le périmètre, en même temps.

Voici donc comment trouver une droite qui divise l’aire et le périmètre en même temps. On commence par trouver une droite qui divise le périmètre en utilisant, par exemple, la méthode décrite ci-dessus. Dans le triangle $ABC$ ci-dessous, d’aire $K$, on considère une telle droite $QR$. Cette droite divise le triangle en deux régions, une à gauche de la droite, d’aire $rK$, et l’autre à droite de la droite, d’aire 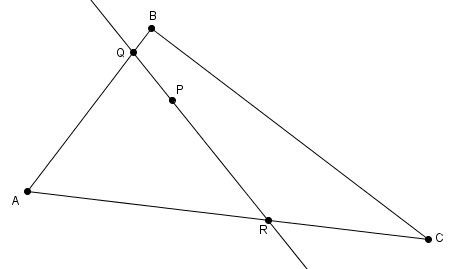$(1-r)K$.

Si la droite $QR$ divise aussi l’aire du triangle, c’est-à-dire si $r=1-r=\frac{1}{2}$, on a gagné ! La droite $QR$ fait l’affaire. Si ce n’est pas le cas, et ce n’est probablement pas le cas, on détermine un sens à la rotation, par exemple antihoraire, et on déplace $Q$ sur le périmètre du triangle sur d’une distance $\delta$ jusqu’à $Q_1$. Pour que la droite partage toujours le périmètre, on déplace aussi $R$ sur le périmètre du triangle, dans le même sens, sur une distance de 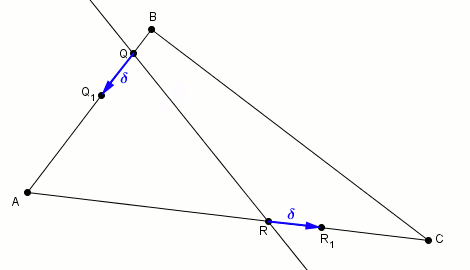$\delta$ jusqu’en $R_1$.

La nouvelle droite $Q_1{R}_1$ partage toujours le périmètre, tout comme la droite $QR$ originale. Qu’arrive-t-il si on prend le demi-périmètre du triangle comme valeur de $\delta$ ? Le point $R$ est envoyé en $Q$ et vice-versa. La région à gauche de la droite se retrouve à droite de celle-ci et vice-versa. Autrement dit, l’aire de la région qui était au départ à gauche est passée de $rK$ à $(1-r)K$. L’aire de la région qui était au départ à droite est passée de $(1-r)K$ à $rK$. Si $r<\frac{1}{2}$, alors $1-r>\frac{1}{2}$ et si $r>\frac{1}{2}$ alors $1-r<\frac{1}{2}$. Les deux régions s’intervertissent leur rôle et, comme dans l’explication précédente, on peut conclure qu’il existe une position intermédiaire (une valeur de $\delta$) pour laquelle les deux régions possèdent la même aire ($r=1-r=\frac{1}{2}$). Voilà !

Sur le nombre de ces droites dans les triangles

Dans un triangle il y a peut-être plus d’une droite qui partage le périmètre et l’aire. Dans un triangle $ABC$, de côtés $a$, $b$, $c$ avec $a<b<c$, il y a une, deux ou trois de ces droites, respectivement, si ${(a+b+c)}^2<2bc$, ${(a+b+c)}^2=2bc$ ou ${(a+b+c)}^2>2bc$.

On considère un triangle $PQR$, de côtés $p$, $q$, $r$ et une droite coupant les côtés de l’angle $P$, à une distance $\theta q$ de $P$ sur le côté de mesure $q$ et une distance ${\theta }_{1}r$ de $P$ sur le côté de mesure $r$. Cette droite partage le périmètre et l’aire, on a ici $\theta$, ${\theta }_1<1$. L’inégalité est stricte, sans quoi la droite considérée passe par un sommet, et pour diviser l’aire il faudrait qu’il s’agisse d’une médiane. Or, puisque le triangle est scalène, la médiane ne partage pas le périmètre (on considérera les triangles équilatéraux et isocèles plus tard).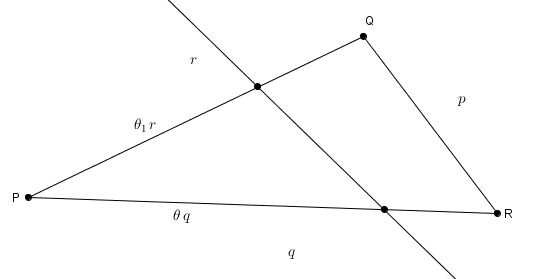

Si la droite partage l’aire en deux parties égales, alors on a $$\begin{array}{rl}\frac{\theta q\cdot {\theta }_{1}r\cdot \sin \left(P\right)}{2}& =\frac{1}{2}\left(\frac{q\cdot r\cdot \sin \left(P\right)}{2}\right)\\ \\ \theta \cdot {\theta }_1\left(\frac{q\cdot r\cdot \sin \left(P\right)}{2}\right)& =\frac{1}{2}\left(\frac{q\cdot r\cdot \sin \left(P\right)}{2}\right)\\ \\ \theta \cdot {\theta }_1& =\frac{1}{2}\end{array}$$ ou, de manière équivalente, $${\theta }_1=\frac{1}{2\theta }$$On note ici qu’il suffit de considérer les valeurs de $\theta$, ${\theta }_1>\frac{1}{2}$. En combinant les deux restrictions, on s’intéresse aux valeurs de $\theta$ et ${\theta }_1$ telles que $$\frac{1}{2}<\theta <1$$et $$\frac{1}{2}<{\theta }_1<1$$

D’autre part, si la droite partage le périmètre, alors on a $$\theta q+{\theta }_{1}r=\frac{p+q+r}{2}$$ou, de manière équivalente, $$2\theta q+2{\theta }_{1}r=p+q+r$$On substitue ${\theta }_1$ par $\frac{1}{2\theta }$ dans l’équation précédente, $$2\theta q+2\left(\frac{1}{2\theta }\right)r=p+q+r$$ce qui fait $$2\theta q+\frac{1}{\theta }r=p+q+r$$On multiplie chaque côté par $\theta$ $$2q{\theta }^2+r=(p+q+r)\theta$$ou, de manière équivalente, $$2q{\theta }^2-(p+q+r)\theta +r=0$$L’équation précédente est une équation quadratique en $\theta$. On considère $$f\left(\theta \right)=2q{\theta }^2-(p+q+r)\theta +r$$pour des valeurs de $$\frac{1}{2}<\theta <1$$On remarque que $$\begin{array}{rl}f\left(\frac{1}{2}\right)& =2q{\left(\frac{1}{2}\right)}^2–(p+q+r)\left(\frac{1}{2}\right)+r\\ \\ & =\frac{1}{2}q-\frac{1}{2}p-\frac{1}{2}q-\frac{1}{2}r+r\\ \\ & =\frac{1}{2}(r-p)\end{array}$$ et aussi que $$\begin{array}{rl}f\left(1\right)& =2q{\left(1\right)}^2-(p+q+r)\left(1\right)+r\\ \\ & =2q-p-q-r+r\\ \\ & =q-p\end{array}$$

D’autre part, en complétant le carré, on obtient $$\begin{array}{rl}f\left(\theta \right)& =2q{\theta }^2-(p+q+r)\theta +r\\ \\ & =2q({\theta }^2-\frac{p+q+r}{2q}\theta +{\left(\frac{p+q+r}{4q}\right)}^2-{\left(\frac{p+q+r}{4q}\right)}^2+\frac{r}{2q})\\ \\ & =2q({(\theta -\frac{p+q+r}{4q})}^2+\frac{r}{2q}-\frac{{(p+q+r)}^2}{16q^2})\\ \\ & =2q{(\theta -\frac{p+q+r}{4q})}^2+r-\frac{{(p+q+r)}^2}{8q}\\ \\ & =2q{(\theta -\frac{p+q+r}{4q})}^2+\frac{8qr-{(p+q+r)}^2}{8q}\end{array}$$

Ainsi, la fonction atteint son minimum en ${\displaystyle \theta =\frac{p+q+r}{4q}}$ et ce minimum est ${\displaystyle \frac{8qr-{(p+q+r)}^2}{8q}}$.

Il nous suffit maintenant d’examiner quelques signes.

Si $P$ joue le rôle de $B$, autrement dit si $p$ joue le rôle de $b$, et on se rappelle que $a<b<c$, alors $$f\left(\frac{1}{2}\right)=\frac{1}{2}(r-p)$$et $$f\left(1\right)=q-p$$sont de signes contraires (si $q<p<r$ alors $r-p$ est strictement positif et $q-p$ est strictement négatif et si $r<p<q$ alors $r-p$ est strictement négatif et $q-p$ est strictement positif). $f\left(\theta \right)$ prend donc la valeur de $0$ sur cet intervalle et il y a dans ce cas toujours une droite qui coupe les côtés $a$ et $c$.

Si $P$ joue le rôle de $C$, autrement dit si $p$ joue le rôle de $c$, le plus grand côté du triangle, alors $$f\left(\frac{1}{2}\right)=\frac{1}{2}(r-p)$$est strictement négatif, $$f\left(1\right)=q-p$$est strictement négatif et $$f\left(\frac{p+q+r}{4q}\right)=\frac{8qr-{(p+q+r)}^2}{8q}$$est aussi strictement négatif. Le dernière affirmation nécessite peut-être une précision. Si $p>q$ alors $$\begin{array}{rl}{(p+q+r)}^2>{(2q+r)}^2& =4q^2+4qr+r^2\\ \\ & =4q^2-4qr+r^2+8qr\\ \\ & ={(2q-r)}^2+8qr\\ \\ & \ge 8qr\end{array}$$ Il n’y a donc aucune valeur de $\theta$ entre $\frac{1}{2}$ et $1$ pour laquelle $f\left(\theta \right)=0$. En d’autres mots, il n’y a aucune droite qui croise les côtés $a$ et $b$.

Enfin, si $P$ joue le rôle de $A$, autrement dit si $p$ joue le rôle de $a$, le plus petit côté du triangle, $$f\left(\frac{1}{2}\right)=\frac{1}{2}(r-p)$$est strictement positif et $$f\left(1\right)=q-p$$est aussi strictement positif. Il y a donc aucune, une ou deux solutions selon la valeur de $$f\left(\frac{p+q+r}{4q}\right)=\frac{8qr-{(p+q+r)}^2}{8q}$$Si $\frac{8qr-{(p+q+r)}^2}{8q}$ est strictement positif, il n’y a aucune valeur pour $\theta$ et aucune droite ne croise les côtés $b$ et $c$. Si $\frac{8qr-{(p+q+r)}^2}{8q}$ est nul, alors il y a une valeur pour $\theta$ (qui, au passage, serait $\theta =\frac{p+q+r}{4q}$) et une droite qui croise les côtés $b$ et $c$. Enfin, si $\frac{8qr-{(p+q+r)}^2}{8q}$ est strictement négatif, il y a deux valeurs pour $\theta$ et deux droites qui croisent les côtés $b$ et $c$.

Comme $8q$ (le dénominateur) est strictement positif, on peut exprimer la condition sous la forme suivante $$8bc-{(a+b+c)}^2\begin{array}{c}>\\ =\\ <\end{array}0$$ou $$8bc\begin{array}{c}>\\ =\\ <\end{array}{(a+b+c)}^2$$ce qui correspond au résultat attendu et énoncé plus haut dans ce billet. En comptant la droite qui croise les côtés $a$ et $c$, on a une, deux ou trois droites selon que, respectivement, $${(a+b+c)}^2\begin{array}{c}<\\ =\\ >\end{array}8bc$$

Si le triangle est équilatéral, on a $a=b=c$ et $${(a+b+c)}^2\begin{array}{c}<\\ =\\ >\end{array}8bc$$devient $${\left(3b\right)}^2\begin{array}{c}<\\ =\\ >\end{array}8b^2$$ou  $$9b^2\begin{array}{c}<\\ =\\ >\end{array}8b^2$$ou $$b^2\begin{array}{c}<\\ =\\ >\end{array}0$$Or comme $b^2$ est strictement positif, il y a toujours trois droites qui coupent le triangle. Ces trois droites sont les trois médianes (le cas $\theta =1$ rejeté ci-haut dans le cas du triangle scalène). Si le triangle est isocèle et que les deux plus petits côtés du triangle sont isométriques, c’est-à-dire que $a=b<c$, alors $${(a+b+c)}^2\begin{array}{c}<\\ =\\ >\end{array}8bc$$devient $${(2b+c)}^2\begin{array}{c}<\\ =\\ >\end{array}8bc$$ce qui fait $$4b^2+4bc+c^2\begin{array}{c}<\\ =\\ >\end{array}8bc$$ou de manière équivalente, $$4b^2-4bc+c^2\begin{array}{c}<\\ =\\ >\end{array}0$$et enfin $${(2b-c)}^2\begin{array}{c}<\\ =\\ >\end{array}0$$Puisque le membre de gauche est toujours strictement positif (pour être nul, il faudrait avoir $a=b=\frac{1}{2}c$, or là, on n’a plus de triangle), il y a toujours trois droites. Enfin, si le triangle est isocèle mais ce sont les deux plus grands côtés qui sont isométriques, alors $a<b=c$ et $${(a+b+c)}^2\begin{array}{c}<\\ =\\ >\end{array}8bc$$devient $${(a+2b)}^2\begin{array}{c}<\\ =\\ >\end{array}8b^2$$Puisque $a$, $b>0$,  $${(a+2b)}^2\begin{array}{c}<\\ =\\ >\end{array}8b^2$$devient $$a+2b\begin{array}{c}<\\ =\\ >\end{array}2\sqrt{2}b$$puis $$a\begin{array}{c}<\\ =\\ >\end{array}(2\sqrt{2}-2)b$$et enfin $$a\begin{array}{c}<\\ =\\ >\end{array}2(\sqrt{2}-1)b$$Puisque $2(\sqrt{2}-1)\approx 0,8284$, mais que néanmoins $0,8284>0,5$, selon la valeur de $a$ et $b=c$, il peut y avoir une, deux ou trois droites comme dans le cas d’un triangle scalène.

Un exemple…

On considère à titre d’exemple le triangle scalène de côtés 40, 45 et 50.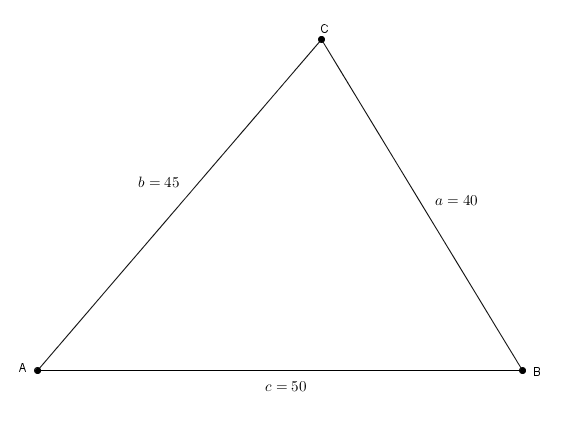Les sommets $A$, $B$ et $C$ et les côtés $a$, $b$ et $c$ sont placés comme il le faut. On constate d’abord que $$\begin{array}{rl}{(40+45+50)}^2& ={135}^2\\ \\ & =18225\\ \\ & >8\left(45\right)\left(50\right)=1800\end{array}$$ Il y a donc 3 droites possibles, une coupant les côtés $a$ et $c$ et deux coupant les côtés $b$ et $c$. En remplaçant par les bonnes valeurs, on trouve d’abord les solutions à $$2\left(50\right){\theta }^2-(40+45+50)\theta +40=0$$ou, de manière équivalente, $$100{\theta }^2-135\theta +40=0$$Les solutions de cette équation quadratique sont $\theta =\frac{27-\sqrt{89}}{40}\approx 0,493$ et $\theta =\frac{27+\sqrt{89}}{40}\approx 0,911$. En se rappelant que $${\theta }_1=\frac{1}{2\theta }$$et que $$\frac{1}{2}<\theta <1$$et $$\frac{1}{2}<{\theta }_1<1$$seule la deuxième solution, $\theta =\frac{27+\sqrt{89}}{40}\approx 0,911$, est acceptée. On trouve, par ailleurs, $$\begin{array}{rl}{\theta }_1& =\frac{1}{2\frac{27+\sqrt{89}}{40}}\\ \\ & =\frac{20}{27+\sqrt{89}}\end{array}$$ puis, en rationalisant,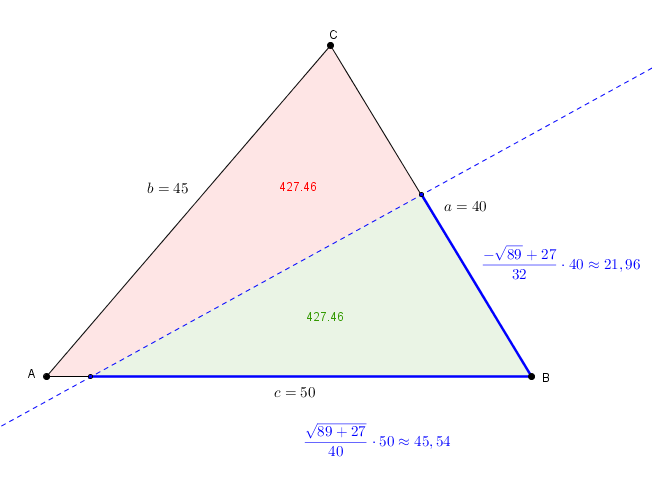 $$\begin{array}{rl}{\theta }_1& =\frac{20(27-\sqrt{89})}{729-89}\\ \\ & =\frac{20(27-\sqrt{89})}{640}\\ \\ & =\frac{27-\sqrt{89}}{32}\approx 0,549\end{array}$$

On trouve ensuite les solutions de $$2\left(50\right){\theta }^2-(40+45+50)\theta +45=0$$ou, de manière équivalente, $$100{\theta }^2–135\theta +45=0$$Cette fois-ci les solutions sont $\theta =\frac{3}{5}$ et $\theta =\frac{3}{4}$ et les deux sont acceptées. La première nous donne ${\theta }_1=\frac{1}{2\left(\frac{3}{5}\right)}=\frac{5}{6}$ et la deuxième ${\theta }_1=\frac{1}{2\left(\frac{3}{4}\right)}=\frac{2}{3}$. Ces valeurs correspondent respectivement à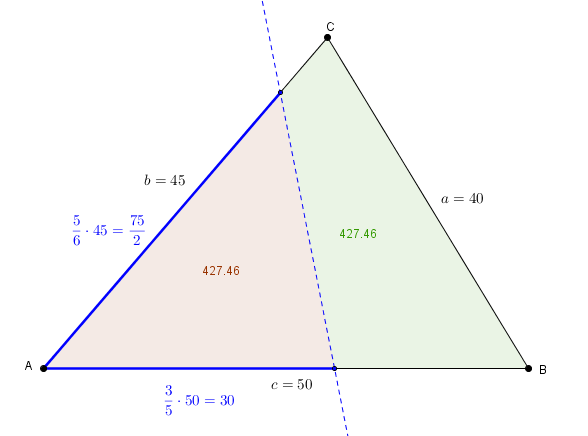et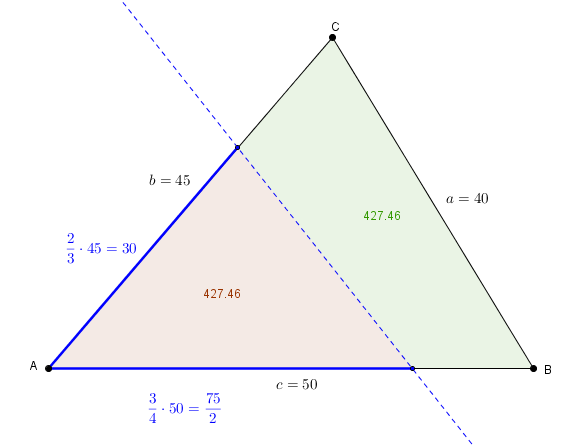

On note au passage, en utilisant ce dernier cas à titre d’exemple, que l’aire du triangle rouge sur la figure est $$\frac{30\cdot \frac{75}{2}\cdot \sin \left(A\right)}{2}=\frac{1125}{2}\cdot \sin \left(A\right)$$ce qui correspond bien à la moitié de l’aire du triangle $ABC$ $$\frac{45\cdot 50\cdot \sin \left(A\right)}{2}=1125\cdot \sin \left(A\right)$$On observe aussi que $$30+\frac{75}{2}=\frac{135}{2}$$correspond aussi à la moitié du périmètre $$40+45+50=135$$

[1] La démarche ci-dessus bien qu’intuitive, n’est pas parfaitement rigoureuse en ce sens qu’elle s’appuie tacitement sur des propriétés fondamentales des nombres réels et sur le théorème des valeurs intermédiaires de fonctions continues qu’on étudierait dans un cours d’analyse.

Références :

Niven, Ivan, Maxima and Minima Without Calculus, MAA, 1981

Dunkel, Otto and E. P. Starke, The American Mathematical Monthly, Vol. 49, pp. 64-68