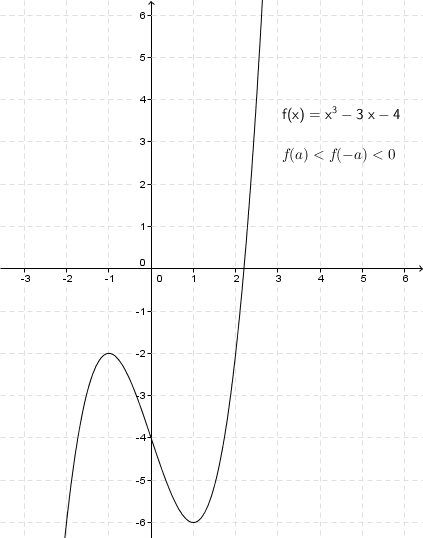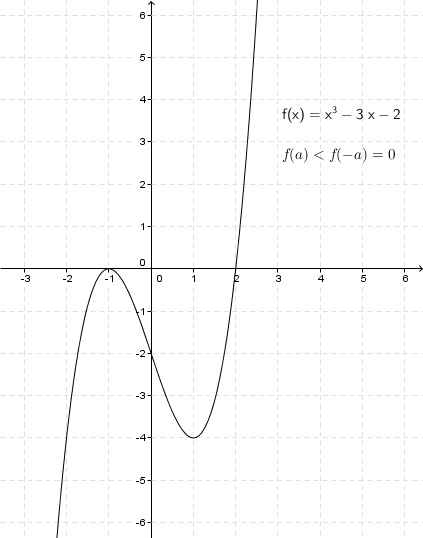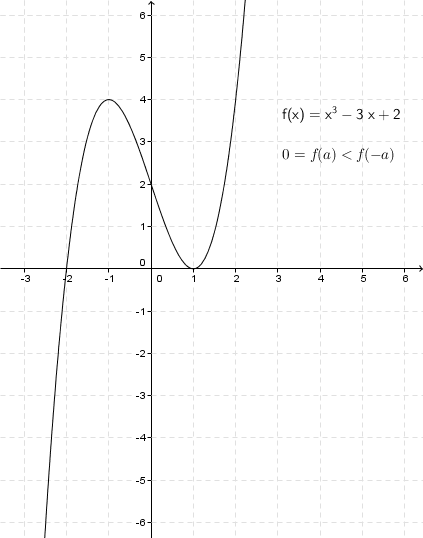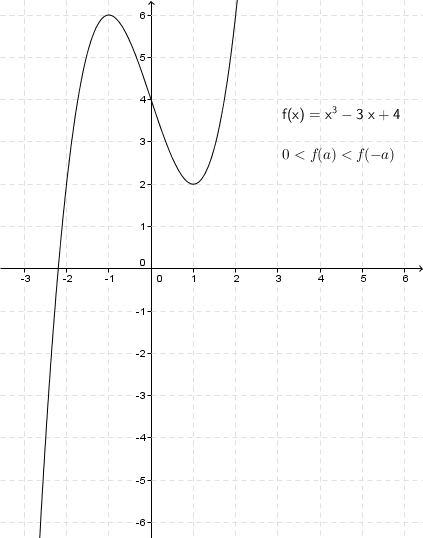Pas de discrimination !

On considère l’équation polynomiale du deuxième degré suivante $$x^2+bx+c=0$$Si le coefficient de $x^2$ est différent de $1$, disons $a$, il suffit, pour obtenir la forme ci-dessus, de diviser chaque terme à gauche et à droite par $a$. Un tel polynôme, dont le coefficient du terme de plus haut degré est $1$, est dit unitaire (monic polynomial en anglais).

Bref, cette équation possède deux solutions, réelles (distinctes ou non) ou complexes (conjugués l’une de l’autre). On appelle ces deux solutions $r$ et $s$ et on considère l’expression $${(r-s)}^2$$Si les deux solutions sont réelles et distinctes, alors il est certain que $${(r-s)}^2>0$$car le carré d’un nombre réel non-nul est toujours strictement positif. Si le polynôme a une solution réelle double, c’est-à-dire si $$r=s$$alors on a évidemment $${(r-s)}^2=0$$Enfin, si les deux solutions sont complexes (dans le sens de non réelles), alors on a $${(r-s)}^2<0$$Ah ? Pourquoi ? Les deux solutions complexes du polynôme sont les conjugués l’une de l’autre. Ainsi en posant, $$\begin{array}{rl}r& =t+ui\\ \\ s& =t-ui\end{array}$$avec $t$ et $u$ réels, on peut calculer $${(r-s)}^2$$et obtenir $$\begin{array}{rl}{(t+ui-(t-ui))}^2& ={(t+ui-t+ui)}^2\\ \\ & ={\left(2ui\right)}^2\\ \\ & =2^2{u}^2{i}^2\\ \\ & =-4u^2\end{array}$$ce qui vérifie effectivement $${(r-s)}^2<0$$puisque $u$ étant non-nul, $u^2$ est strictement positif et $-4u^2$ strictement négatif. On peut donc considérer, à juste titre, l’expression $$\delta ={(r-s)}^2$$que l’on baptise $\delta$ et qui met en vedette les solutions de l’équation, comme un discriminant de l’équation : le signe de $\delta$ détermine si l’équation du départ possède deux solutions réelles distinctes ($\delta$ est strictement positif), une solution réelle double ($\delta$ est nul) ou deux solutions complexes ($\delta$ est strictement négatif).

C’est cependant un peu embêtant de devoir connaître $r$ et $s$ pour découvrir la nature de… $r$ et $s$. Qui plus est, on connaît notre bon vieux $$\mathrm{\Delta }=b^2-4c$$calculé commodément à partir des coefficients de l’équation initiale. Mais voilà, on peut établir un lien entre $\delta$ et $\mathrm{\Delta }$. En effet, si $r$ et $s$ sont les solutions, alors notre polynôme unitaire se factorise comme $$x^2+bx+c=(x-r)(x-s)$$ce qui donne en développant $$\begin{array}{rl}{x}^2+bx+c& =(x-r)(x-s)\\ \\ & =x^2-rx-sx+rs\\ \\ & =x^2-(r+s)x+rs\end{array}$$et on trouve ainsi $$\begin{array}{rl}b& =-(r+s)\\ \\ c& =rs\end{array}$$

Par ailleurs, $$\begin{array}{rl}{(r-s)}^2& =r^2-2rs+s^2\\ \\ & =r^2-2rs+s^2+4rs-4rs\\ \\ & =r^2+2rs+s^2-4rs\\ \\ & ={(r+s)}^2-4rs\\ \\ & ={(-(r+s))}^2-4rs\end{array}$$ et en remplaçant par $b$ et $c$ on obtient $$\begin{array}{rl}{(r-s)}^2& ={(-(r+s))}^2-4rs\\ \\ & =b^2-4c\end{array}$$Ah ! On a donc $$\begin{array}{rl}{(r-s)}^2& =b^2-4c\\ \\ \delta & =\mathrm{\Delta }\end{array}$$Fascinant ! L’intérêt de considérer le discriminant sous cette forme est que cette technique s’applique aux équations polynomiales de degrés supérieurs à 2 : on peut donc trouver des discriminants pour ces équations et tirer des informations sur les solutions à partir des coefficients. On considère à titre d’exemple la forme réduite de l’équation polynomiale de degré 3 suivante (au besoin, on peut toujours réduire) $$x^3+px+q=0$$C’est aussi une équation unitaire. Cette équation possède 3 solutions réelles distinctes, 2 solutions réelles distinctes (dont une double) ou 1 solution réelle et 2 complexes (toujours dans le sens de non-réelles, et qui sont les conjugués l’une de l’autre).

La méthode “intuitive”

Pour chercher de l’information sur les zéros et en utilisant un minimum (!) de calcul différentiel, on pourrait étudier la fonction $$f(x)=x^3+px+q$$Cette équation polynomiale unitaire de degré impair passe du négatif pour des valeurs de $x$ suffisamment petites au positif pour des valeurs de $x$ suffisamment grandes. Elle possède aussi au plus deux changements de croissance/décroissance.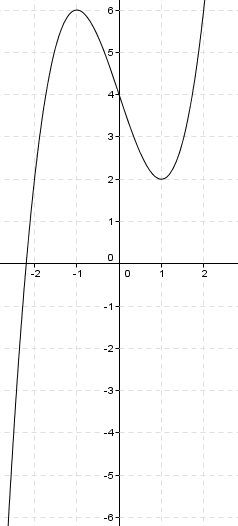L’étude de cette fonction, sans le terme en $x^2$, est par ailleurs assez facile. La dérivée de cette fonction est $$f^{\prime }(x)=3x^3+p$$En posant la dérivée égale à $0$ $$3x^2+p=0$$on trouve les abscisses des extrema $$x=\pm \sqrt{-\frac{p}{3}}$$En posant $$a=\sqrt{-\frac{p}{3}}$$comme la racine positive, on peut déduire les résultats suivants. Si $$f(a)<f(-a)<0$$alors la fonction possède un zéro réel et deux zéros complexes. Si $$f(a)<f(-a)=0$$alors la fonction possède deux zéros réels distincts, dont un zéro double. Si $$f(a)<0<f(-a)$$alors la fonction possède trois zéros réels distincts. Si $$0=f(a)<f(-a)$$alors la fonction possède deux zéros réels distincts, dont un zéro double. Enfin si $$0<f(a)<f(-a)$$la fonction possède un zéro réel et deux zéros complexes.

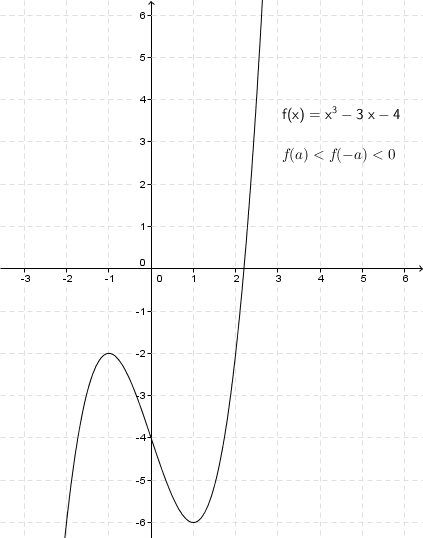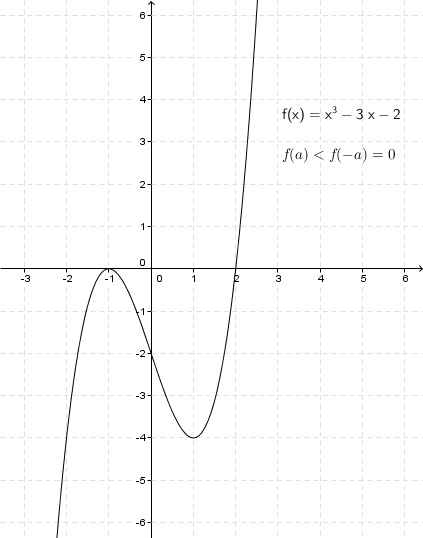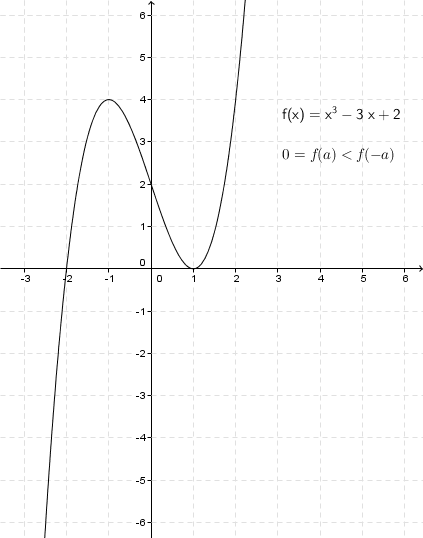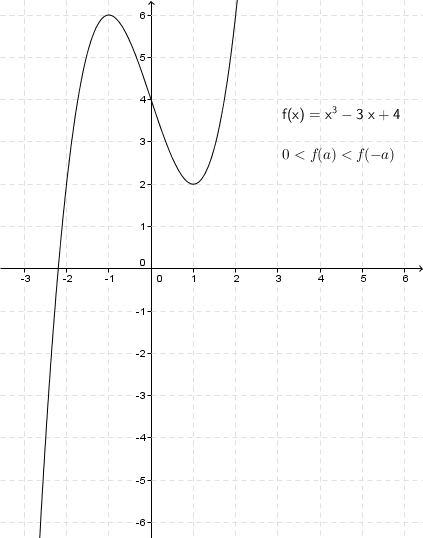
On peut réécrire les cinq cas précédents de manière plus concise en ayant recours de manière astucieuse à la loi des signes et en vérifiant que les trois cas suivants sont équivalents. Si $$f(-a)f(a)>0$$alors la fonction possède un zéro réel et deux complexes. Si $$f(-a)f(a)=0$$alors la fonction possède deux zéros réels distincts, dont un zéro double. Enfin si $$f(-a)f(a)<0$$alors la fonction possède trois zéros réels distincts. Pour le calcul de $f(-a)f(a)$, il suffit de multiplier $$f(-a)f(a)=({(-a)}^3+p(-a)+q)({\left(a\right)}^3+p\left(a\right)+q)$$et de quelques étapes algébriques assez simples mais un peu fastidieuses $$\begin{array}{rl}f(-a)f(a)& =({(-a)}^3+p(-a)+q)({\left(a\right)}^3+p\left(a\right)+q)\\ \\ & =({(-a)}^2\cdot (-a)-pa+q)(a^2\cdot a+pa+q)\\ \\ & =((-\frac{p}{3})\cdot (-a)-pa+q)((-\frac{p}{3})\cdot a+pa+q)\\ \\ & =(\left(\frac{p}{3}\right)\cdot a-pa+q)((-\frac{p}{3})\cdot a+pa+q)\\ \\ & =((\frac{p}{3}-p)a+q)((-\frac{p}{3}+p)a+q)\\ \\ & =(-\frac{2p}{3}a+q)(\frac{2p}{3}a+q)\\ \\ & =-\frac{4p^2}{9}{a}^2-\frac{2pq}{3}a+\frac{2pq}{3}a+q^2\\ \\ & =-\frac{4p^2}{9}(-\frac{p}{3})+q^2\\ \\ & =\frac{4p^3}{27}+q^2\end{array}$$On multiplie par $-27$, pour des raisons qui ne sont peut-être pas claires pour l’instant, mais qui le deviendront plus tard. Multiplier par $27$, oui, pour se débarrasser du dénominateur, mais $-27$ ? On obtient $$-27f(-a)f(a)=-4p^3-27q^2$$On pose $$\mathrm{\Delta }=-4p^3-27q^2$$notre discriminant, et, puisqu’on a multiplié $f(-a)f(a)$ par un nombre négatif, on change les signes de côté dans les inéquations précédentes. Ainsi, toujours avec $$x^3+px+q=0$$si $$\mathrm{\Delta }<0$$alors l’équation possède une solution réelle et deux solutions complexes. Si $$\mathrm{\Delta }=0$$alors l’équation possède deux solutions réelles distinctes, dont une solution double. Enfin si $$\mathrm{\Delta }>0$$alors l’équation possède trois solutions réelles distinctes.

La méthode des zéros

De manière analogue à ce qu’on avait fait avec l’équation du deuxième degré, on considère l’expression $$\delta ={(r-s)}^2{(r-t)}^2{(s-t)}^2$$où $r$, $s$ et $t$ sont les trois solutions à l’équation. Les solutions d’une équation réduite du troisième degré ont la forme $$\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}$$c’est-à-dire la somme de deux racines cubiques. On pose $$r=A+B$$où $A=\sqrt[3]{-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}$ et $B=\sqrt[3]{-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}}$ sont les racines cubiques telle que $r$ est réel (il y a toujours au moins une racine réelle à une équation du troisième degré). En d’autres mots, on choisit $A$ et $B$ tels que $$AB=-\frac{p}{3}$$Il est connu qu’on peut exprimer les deux autres solutions en fonction de $A$ et $B$. Ces solutions sont $$s=\omega A+{\omega }^{2}B,t={\omega }^{2}A+\omega B$$et dans lesquelles $$\omega =\frac{-1+\sqrt{3}i}{2}$$et $${\omega }^2=\frac{-1-\sqrt{3}i}{2}$$sont les racines cubiques de l’unité. Le calcul de  $${(r-s)}^2{(r-t)}^2{(s-t)}^2$$peut s’avérer fort fastidieux alors on fait preuve d’astuce. On peut vérifier que $$\begin{array}{rl}r-s& =A+B-(\omega A+{\omega }^{2}B)\\ \\ & =A-\omega A+B-{\omega }^{2}B\end{array}$$Comme $${\omega }^3=1$$on peut effectuer une mise en évidence double et trouver $$\begin{array}{rl}r-s& =A-\omega A+B-{\omega }^{2}B\\ \\ & =A-\omega A+{\omega }^{3}B-{\omega }^{2}B\\ \\ & =A(1-\omega )-{\omega }^{2}B(1-\omega )\\ \\ & =(1-\omega )(A-{\omega }^{2}B)\end{array}$$De la même manière, on trouve$$\begin{array}{rl}r-t& =A+B-({\omega }^{2}A+\omega B)\\ \\ & =A-{\omega }^{2}A+B-\omega B\\ \\ & ={\omega }^{3}A-{\omega }^{2}A+{\omega }^{3}B-{\omega }^{4}B\\ \\ & =-{\omega }^2(A-\omega A-\omega B+{\omega }^{2}B)\\ \\ & =-{\omega }^2(A(1-\omega )-\omega B(1-\omega ))\\ \\ & =-{\omega }^2(1-\omega )(A-\omega B)\end{array}$$et $$\begin{array}{rl}s-t& =\omega A+{\omega }^{2}B-({\omega }^{2}A+\omega B)\\ \\ & =\omega A-{\omega }^{2}A+{\omega }^{2}B-\omega B\\ \\ & =\omega (A-\omega A+\omega B-B)\\ \\ & =\omega (A(1-\omega )-B(1-\omega ))\\ \\ & =\omega (1-\omega )(A-B)\end{array}$$Enfin, on a un dernier ingrédient, $$\begin{array}{rl}{(1-\omega )}^3& =1-3\omega +3{\omega }^2-{\omega }^3\\ \\ & =1-3\omega +3{\omega }^2-1\\ \\ & =-3\omega +3{\omega }^2\\ \\ & =3({\omega }^2-\omega )\end{array}$$qui donne finalement $$\begin{array}{rl}{(1-\omega )}^3& =3({\omega }^2-\omega )\\ \\ & =3(\frac{-1-\sqrt{3}i}{2}-\frac{-1+\sqrt{3}i}{2})\\ \\ & =3\left(\frac{-2\sqrt{3}i}{2}\right)\\ \\ & =-3\sqrt{3}i\end{array}$$Ainsi, en remplaçant dans l’expression de $\delta$, $${(r-s)}^2{(r-t)}^2{(s-t)}^2={\left({(r-s)}^2(r-t)(s-t)\right)}^2$$on obtient $$\begin{array}{rl}{(r-s)}^2{(r-t)}^2{(s-t)}^2& ={\left((r-s)(r-t)(s-t)\right)}^2\\ \\ & ={\left(3\sqrt{3}i(A-{\omega }^{2}B)(A-\omega B)(A-B)\right)}^2\\ \\ & ={\left(3\sqrt{3}i(A^3-A^{2}B-\omega A^{2}B+\omega A{B}^2-{\omega }^2{A}^{2}B+{\omega }^{2}A{B}^2+{\omega }^{3}A{B}^2-{\omega }^3{B}^3)\right)}^2\\ \\ & ={\left(3\sqrt{3}i(A^3-B^3-(1+\omega +{\omega }^2)A^{2}B+(1+\omega +{\omega }^2)A{B}^2)\right)}^2\end{array}$$Or comme $$\begin{array}{rl}1+\omega +{\omega }^2& =1+\frac{-1+\sqrt{3}i}{2}+\frac{-1-\sqrt{3}i}{2}\\ \\ & =1-\frac{2}{2}\\ \\ & =0\end{array}$$l’expression précédente devient $$\begin{array}{rl}{(r-s)}^2{(r-t)}^2{(t-s)}^2& ={\left(3\sqrt{3}i(A^3-B^3-(1+\omega +{\omega }^2)A^{2}B+(1+\omega +{\omega }^2)A{B}^2)\right)}^2\\ \\ & ={\left(3\sqrt{3}i(A^3-B^3)\right)}^2\end{array}$$Ouf ! En se rappelant que $A$ et $B$ étaient les racines cubiques, on trouve finalement $$\begin{array}{rl}{(r-s)}^2{(r-t)}^2{(t-s)}^2& ={\left(3\sqrt{3}i(A^3-B^3)\right)}^2\\ \\ & =-27{(-\frac{q}{2}+\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}-(-\frac{q}{2}-\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}))}^2\\ \\ & =-27{\left(2\sqrt{{\left(\frac{q}{2}\right)}^2+{\left(\frac{p}{3}\right)}^3}\right)}^2\\ \\ & =-27(4{\left(\frac{q}{2}\right)}^2+4{\left(\frac{p}{3}\right)}^3)\\ \\ & =-27(\frac{4q^2}{4}+\frac{4p^3}{27})\\ \\ & =-27(q^2+\frac{4p^3}{27})\end{array}$$Et c’est non sans un certain plaisir qu’on distribue le $-27$ à l’intérieur des parenthèses pour obtenir $$\begin{array}{rl}{(r-s)}^2{(r-t)}^2{(t-s)}^2& =-27(q^2+\frac{4p^3}{27})\\ \\ & =-4p^3-27q^2\end{array}$$le discriminant de l’équation polynomiale réduite du troisième degré. Et encore une fois, on constate que $$\delta =\mathrm{\Delta }$$

Référence : Ron Irving, (2013) Beyond the Quadratic Formula