Plus tôt cette année, un peu avant la journée de \(\pi\), j’ai vu dans une infolettre mathématique hebdomadaire cette rubrique :
Je dois avouer que l’infolettre est d’ordinaire assez bien ficelée et que je trouve les contenus souvent intéressants et pertinents, surtout pour un enseignant au secondaire. Sans surprise j’étais donc enthousiasmé par la suite présentée, une suite simple, nouvelle en ce qui me concerne, et qui tend vers une constante célébrée. Je l’ai donc soumise avec entrain à certains élèves qui étaient encore dans la classe au moment où j’ai consulté l’infolettre. J’ai même osé dire à un élève dont je savais les parents professeurs de mathématiques : « Tiens, tu montreras ça à ton père ! Je ne sais pas encore pourquoi ça tend vers \(\pi\), mais c’est intriguant ! »
Curieux de connaître la rapidité avec laquelle la suite converge vers \(\pi\), en arrivant à la maison j’ai concocté un petit script en python :
Aïe aïe aïe ! J’ai été surpris de constater qu’en réalité la suite ne tend pas vers \(\pi\), malgré ce qu’insinuait l’infolettre. Elle semble tendre vers un autre nombre pas loin, à près de \(0,\!00005\) de \(\pi\). Close, but no cigar. Oups ! Un petit courriel plus tard pour expliquer mon trop plein d’enthousiasme (et la bévue) au père de mon élève, et je me mettais au travail. « … numbers that converge to a recognisable number ». Ah ? Lequel ? Je ne vois pas.
Feu l’Inverseur de Plouffe
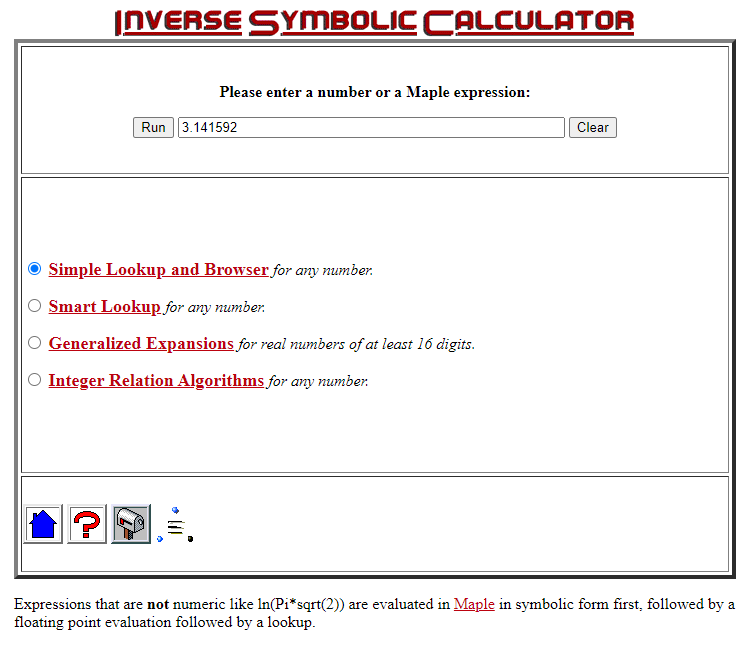
Étant incapable d’utiliser à bon escient la référence du Journal of Recreational Mathematics, mon premier réflexe a été de tenter de me rendre sur le site de l’Inverseur de Plouffe, pour voir si ce nombre mystère s’y trouvait. Je dis « tenter » car c’est à ce moment que j’ai découvert que l’Inverseur de Plouffe n’est plus en ligne… depuis… 12 ans. Re-oups. Ça ne nous rajeunit pas, disons.
La fraction médiane ? (non)
Je dois avouer que j’ai ensuite passé un peu (trop) de temps à investiguer du côté des fractions médianes. La fraction médiane de \(\frac{a}{b}\) et \(\frac{c}{d}\) est \(\frac{a+c}{b+d}\). Et dans la suite, on somme les dividendes (numérateurs) et les diviseurs (dénominateurs) des deux termes précédents. On note parfois \(\oplus\) l’opération de faire la somme des numérateurs et des dénominateurs \[\frac{a}{b}\oplus \frac{c}{d} = \frac{a+c}{b+d}\]que les anglophones nomment « the freshman’s sum » parce qu’il s’agit d’une façon erronée d’effectuer l’addition (traditionnelle) de fractions, erreur que répètent parfois certains élèves novices. L’intérêt de la fraction médiane est que si \[\frac{a}{b}<\frac{c}{d}\] et que \(a\), \(b\), \(c\) et \(d\) sont positifs, alors \[\frac{a}{b}<\frac{a+c}{b+d}<\frac{c}{d}\]
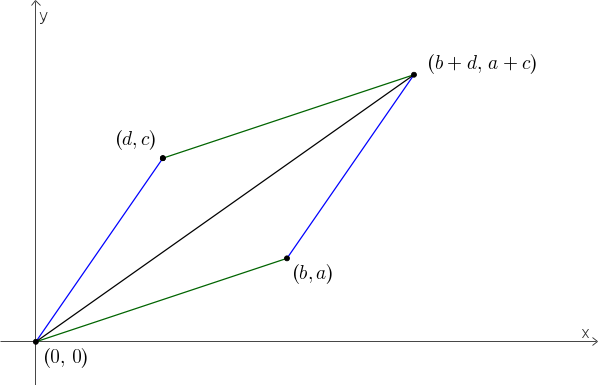
Les pentes des côtés du parallélogramme sont \(\frac{a}{b}\) et \(\frac{c}{d}\) et \(\frac{a}{b}<\frac{c}{d}\).
La pente de la diagonale du parallélogramme est \(\frac{a+c}{b+d}\) et \(\frac{a}{b}<\frac{a+c}{b+d}<\frac{c}{d}\).
On peut s’en convaincre algébriquement en calculant les différences strictement positives entre \(\frac{a+c}{b+d}\) et \(\frac{a}{b}\) \begin{align*}\frac{a+c}{b+d}-\frac{a}{b} &=\frac{b(a+c)}{b(b+d)}-\frac{a(b+d)}{b(b+d)} \\ \\ &=\frac{ab+bc}{b^{2}+bd}-\frac{ab+ad}{b^{2}+bd} \\ \\ &= \frac{ab + bc-ab-ad}{b^{2}+bd} \\ \\ &=\frac{bc-ad}{b^{2}+bd}\\ \\ &=\frac{\frac{bc}{bd}-\frac{ad}{bd}}{\frac{b^{2}}{bd}+\frac{bd}{bd}} \\ \\ &= \frac{\frac{c}{d}-\frac{a}{b}}{\frac{b}{d}+1} > 0 \end{align*}car \begin{align*}\frac{c}{d}&>\frac{a}{b} \\ \\ \frac{c}{d}-\frac{a}{b}&>0\end{align*}et \[\frac{b}{d}+1>0\]et entre \(\frac{c}{d}\) et \(\frac{a+c}{b+d}\) \begin{align*}\frac{c}{d}-\frac{a+c}{b+d}&=\frac{c(b+d)}{d(b+d)}-\frac{d(a+c)}{d(b+d)}\\ \\ &=\frac{bc+cd}{bd+d^{2}}-\frac{ad+cd}{bd+d^{2}}\\ \\ &=\frac{bc+cd-ad-cd}{bd+d^{2}} \\ \\ &=\frac{bc-ad}{bd+d^{2}} \\ \\ &=\frac{\frac{bc}{bd}-\frac{ad}{bd}}{\frac{bd}{bd}+\frac{d^{2}}{bd}} \\ \\ &=\frac{\frac{c}{d}-\frac{a}{b}}{1+\frac{d}{b}} > 0\end{align*} car \[\frac{c}{d}-\frac{a}{b}>0\] et \[1+\frac{b}{d}>0\]Les fractions médianes peuvent donc nous servir à trouver des approximations rationnelles à des nombres irrationnels sans trop de peine. Par exemple, pour \(\pi\), on peut utiliser les fractions \(\frac{3}{1}\) et \(\frac{4}{1}\) puisque \[\frac{3}{1}<\pi< \frac{4}{1}\]La première fraction médiane est \[\frac{3}{1}\oplus \frac{4}{1}=\frac{3+4}{1+1} = \frac{7}{2}\]Puisque \[\frac{3}{1}< \pi <\frac{7}{2}\]la deuxième fraction médiane serait \[\frac{3}{1}\oplus\frac{7}{2} = \frac{3+7}{1+3} = \frac{10}{3}\]Puisque \[\frac{3}{1}<\pi <\frac{10}{3}\]la suivante serait \[\frac{3}{1}\oplus \frac{10}{3} = \frac{10+3}{1+3} = \frac{13}{4}\]Puis comme \[\frac{3}{1}<\pi <\frac{13}{4}\]la suivante serait \[\frac{3}{1}\oplus \frac{13}{4} = \frac{3+13}{1+4} = \frac{16}{5}\]Puisque \(\pi\) était beaucoup plus près de la fraction de départ \(\frac{3}{1}\) que de la fraction de départ \(\frac{4}{1}\), on semble s’approcher de \(\pi\) par la droite, en d’autres mots, la fraction médiane est pour l’instant toujours supérieure à \(\pi\). Bien sûr, cela ne sera pas toujours le cas. Poursuivons encore quelques étapes,\[\frac{3}{1}<\pi <\frac{16}{5}\]nous donne \[\frac{3}{1}\oplus \frac{16}{5} = \frac{3+16}{1+5} =\frac{19}{6}\]puis \[\frac{3}{1}<\pi <\frac{19}{6}\]nous donne \[\frac{3}{1}\oplus \frac{19}{6} = \frac{22}{7}\]approximation célébrée de \(\pi\). \[\frac{3}{1}<\pi <\frac{22}{7}\]nous donne une enième approximation par la droite \[\frac{3}{1}\oplus \frac{22}{7} = \frac{3+22}{1+7} = \frac{25}{8}\]avant que \[\frac{22}{7}<\pi <\frac{25}{8}\]nous donne une première approximation par la gauche \[\frac{22}{7}\oplus\frac{25}{8} = \frac{25+22}{7+8} = \frac{47}{15}\]Les approximations obtenues avec les fractions médianes sont sensibles au choix des fractions de départ et convergent lentement par rapport à d’autres méthodes. Les meilleures approximations rationnelles sont celles obtenues à l’aide des fractions continues, et en comparaison, celles des fractions médianes font pâle figure. Il nous a fallu de nombreuses étapes pour trouver \[\frac{47}{15}\approx 3,\!1333\]une approximation qui n’est pas, en soi, exceptionnelle.
En outre, dans la suite,
en considérant les divisions comme des fractions, on approche le nombre mystère en trouvant la fraction médiane des deux dernier termes. Or, sans plan clair et agacé par le fait qu’on utilise uniquement les deux dernières fractions et jamais celle qui précède les deux dernières, comme c’est arrivé dans mon exemple pour \(\pi\), j’ai eu l’impression d’emprunter un cul-de-sac. Or, ce n’était pas en vain : à quelle notion pourrait-on faire référence lorsqu’on considère les sommes des deux derniers termes ?
La suite de Fibonacci (oui !)
En effet, si on considère la suite de Fibonacci, \[1, \ 1, \ 2, \ 3, \ 5, \ 8, \ 13, \ 21, \ 34, \ 55, \ 89, \ 144, \ 233, \ 377, \ 610\, \ \dots\]on peut observer que les diviseurs correspondent aux quintuple des termes de de la suite.\[\textcolor{Red}{5}, \ \textcolor{Red}{5}, \ 10, \ 15, \ 25, \ 40, \ 65, \ 105, \ 170, \ 275, \ 445, \ 720, \ , 1\,165,\ 1\,885, \ 3\,050\, \ \dots\]Pour les dividendes, c’est moins évident, mais ce sont les sextuple des termes de la suite, avec un déphasage \[6, \ 6, \ \textcolor{Blue}{12}, \ \textcolor{Blue}{18}, \ 30, \ 48, \ 78, \ 126, \ 204, \ 330, \ 534, \ 864, \ 1\,398, \ 2\,262, \ 3\,660\, \ \dots\]Si \(F_{n}\) représente le \(n^{\text{e}}\) terme de la suite de Fibonacci, alors les termes de la suite de l’infolettre sont \[\displaystyle \frac{6F_{n+2}}{5F_{n}}\]En se rappelant que \(F_{n+2} = F_{n+1}+F_{n}\), o peut évaluer la limite \begin{align*}\lim_{n\to \infty}\frac{6F_{n+2}}{5F_{n}}&=\frac{6}{5}\cdot \lim_{n\to \infty}\frac{F_{n+2}}{F_{n}} \\ \\ &=\frac{6}{5}\cdot \lim_{n\to \infty}\frac{F_{n+1}+F_{n}}{F_{n}} \\ \\ &= \frac{6}{5}\left( \lim_{n\to \infty} 1 + \frac{F_{n+1}}{F_{n}}\right) \\ \\ &=\frac{6}{5}\left(1+\lim_{n \to \infty}\frac{F_{n+1}}{F_{n}}\right)\\ \\ &= \frac{6}{5}\left(1 + \varphi\right)\end{align*}car tel que vu précédemment sur ce blogue, le rapport des termes consécutifs de la suite tendent vers \(\varphi = \frac{1+\sqrt{5}}{2}\). Sachant en plus que \begin{align*}1 + \varphi &= 1+ \frac{1+\sqrt{5}}{2} \\ \\ &=\frac{3+\sqrt{5}}{2} \\ \\ &= \frac{6+2\sqrt{5}}{4} \\ \\ &= \frac{1+2\sqrt{5}+5}{4} \\ \\ &=\frac{(1+\sqrt{5})^{2}}{2^{2}} \\ \\ &=\left(\frac{1+\sqrt{5}}{2}\right)^{2} \\ \\ &=\varphi^{2}\end{align*}il est possible d’écrire \[\frac{6}{5}\left(1+\varphi\right) = \frac{6}{5}\varphi^{2}\]La suite tend donc vers \[\frac{6}{5}\varphi^{2} = \frac{9+3\sqrt{5}}{5} \approx 3,\!141640786499873817845504201238\]un nombre qui est à moins de \(0,\!000048132910080579383\) de \(\pi\). Grâce à cette valeur, je suis ensuite tombé sur cette page chez Futility Closet, contenant la même référence au Journal of Recreational Mathematics, mais hélas sans plus de détails.
PS. Au moment où j’allais publier le billet, j’ai découvert une version de l’Inverseur disponible ici : http://wayback.cecm.sfu.ca/projects/ISC/ISCmain.html
J’avais foi en l’Inverseur et j’aurai eu raison ! En effet, on y trouve :
\[18 + 6\sqrt{5} \approx 31,\!41640786499873817\]ce qui nous aurait bien sûr mis sur la bonne piste.