Quatre cercles et un triangle équilatéral

L’édition 2022 du concours Opti-Math+ demandait aux élèves les questions suivantes :

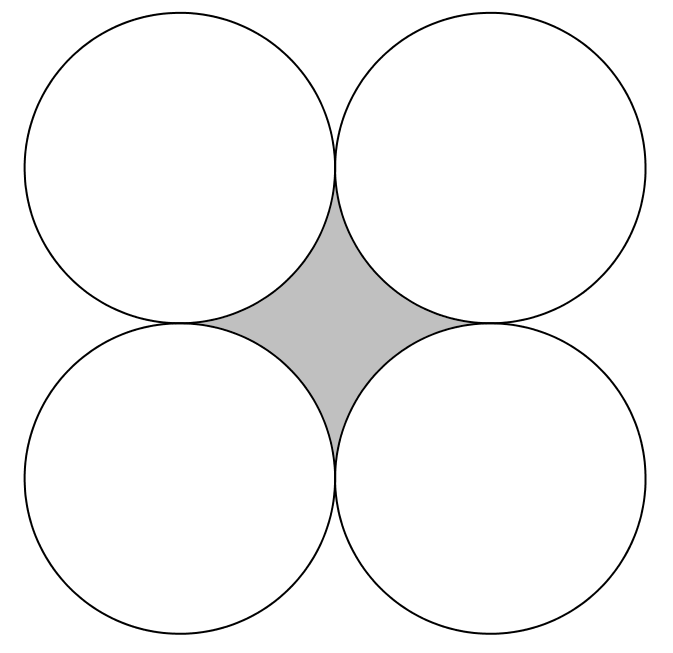
Soit quatre cercles isométriques tangents de 10 cm de diamètre disposés comme dans l’image suivante :

a) Quelle serait l’aire du plus grand cercle qu’on pourrait dessiner dans la zone grise ?

b) Quelle serait l’aire du plus grand triangle équilatéral qu’on pourrait dessiner dans la zone grise ?

 

Le cercle de la zone grise

La première question en est une assez classique pour ce type de concours. On peut tracer des rayons et former un triangle rectangle (au fait, pourquoi le triangle $O_1{O}_2{O}_3$ est-il rectangle ?)

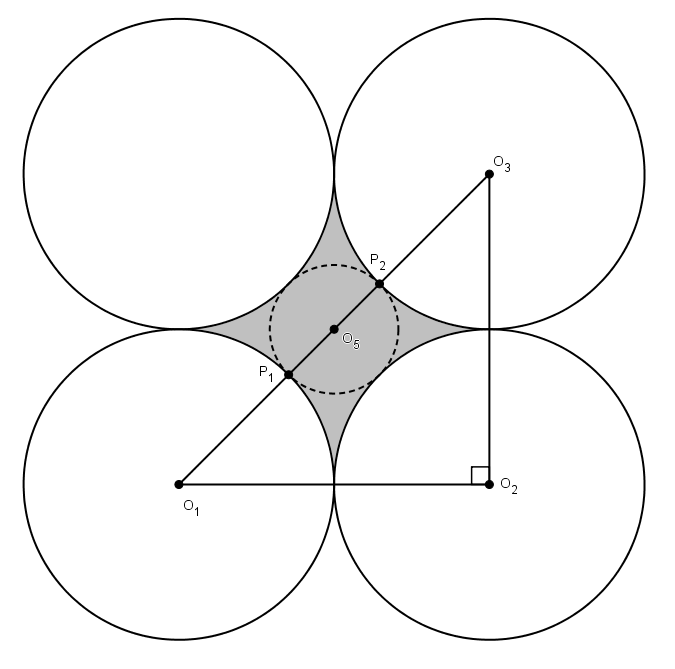
Puisque ces segments $O_1{O}_2$ et $O_2{O}_3$ correspondent à deux rayons, donc à un diamètre, on a $$m\overline{O_1{O}_2}=m\overline{O_2{O}_3}=10$$cm. Cela nous permet de trouver la mesure de $\overline{O_1{O}_3}$, en cm, avec la relation de Pythagore $$\begin{array}{rl}{\left(m\overline{O_1{O}_2}\right)}^2+{\left(m\overline{O_2{O}_3}\right)}^2& ={\left(m\overline{O_1{O}_3}\right)}^2\\ \\ {10}^2+{10}^2& ={\left(m\overline{O_1{O}_3}\right)}^2\\ \\ 200& ={\left(m\overline{O_1{O}_3}\right)}^2\\ \\ \sqrt{200}& =m\overline{O_1{O}_3}\\ \\ 10\sqrt{2}& =m\overline{O_1{O}_3}\end{array}$$Puisque les segments $O_1{P}_1$ et $O_2{P}_2$ sont des rayons, leur mesure est de $5$ cm. Le diamètre du cercle de la région grise (tracé en pointillé) est donc $$\begin{array}{rl}m\overline{P_1{P}_2}& =m\overline{O_1{O}_3}-m\overline{O_1{P}_1}-m\overline{O_3{P}_2}\\ \\ & =10\sqrt{2}-2\cdot 5\\ \\ & =10(\sqrt{2}-1)\end{array}$$cm et son rayon $$\begin{array}{rl}10(\sqrt{2}-1)÷2& =5(\sqrt{2}-1)\\ \\ & =5\sqrt{2}-5\end{array}$$cm. On peut répondre à la question. L’aire, en cm², est $$\begin{array}{rl}\text{Aire du triangle}& =\pi \cdot {(5\sqrt{2}-5)}^2\\ \\ & =\pi \cdot (50-50\sqrt{2}+25)\\ \\ & =\pi \cdot (75-50\sqrt{2})\\ \\ & \approx 13,4753\end{array}$$

Le triangle de la zone grise

J’étais un peu perplexe, lorsque j’ai essayé de faire l’épreuve seul, concernant la deuxième question. Cela me semblait difficile et je ne voyais pas d’amorce de solution simple. Le corrigé sur le site du concours prétend toujours au moment d’écrire ces lignes que le plus grand triangle équilatéral est inscrit dans le cercle pointillé décrit à la question précédente.

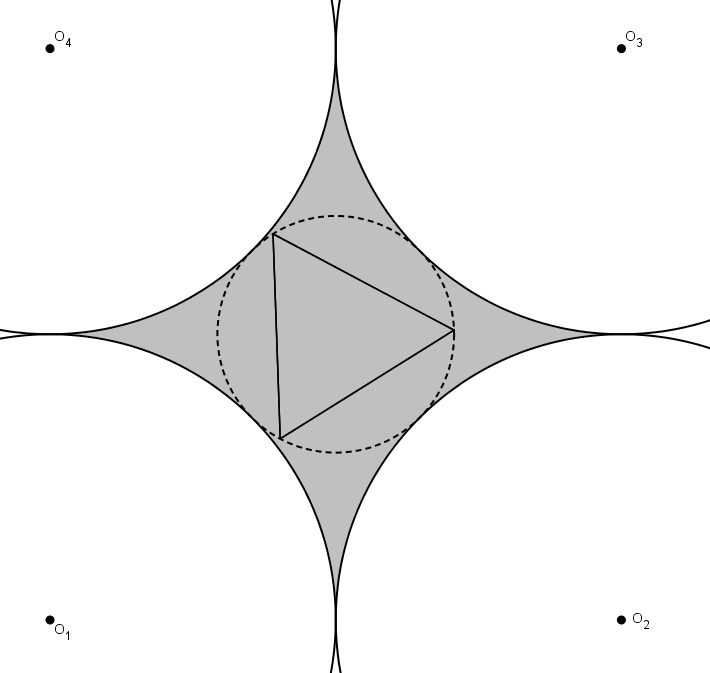
Son aire serait donc d’environ 9,9 cm² selon le corrigé (ou exactement $\frac{100\sqrt{3}(3-2\sqrt{2})}{3}$ cm² si on effectue les calculs et conserve les valeurs exactes). Or, en s’amusant un peu dans Géogébra, on découvre facilement des triangles dont les aires sont supérieures. Qu’en est-il en fait ?

Une démarche intuitive

Je me permets de partager ma démarche qui n’a pas le mérite d’être en tout point rigoureuse mais qui devrait convaincre, je l’espère, un élève du secondaire perplexe.

Il est possible de trouver des triangles équilatéraux inscrits dans ce cercle pointillé qui ne sont ni tangents aux grands cercles et qui ne lui touchent pas non plus par un de leurs sommets.

On peut « gonfler » un de ces triangles jusqu’à ce qu’un de ses côtés soit tangent à un grand cercle ou jusqu’à ce qu’un de ses sommets touchent un des grands cercles obtenant du même coup un triangle d’aire supérieure.

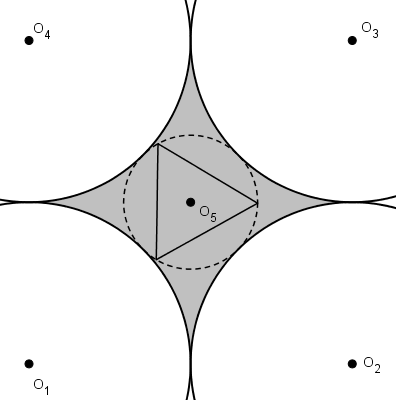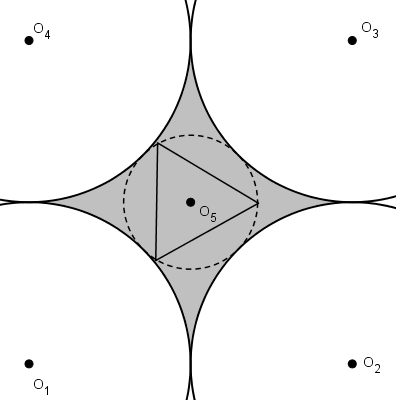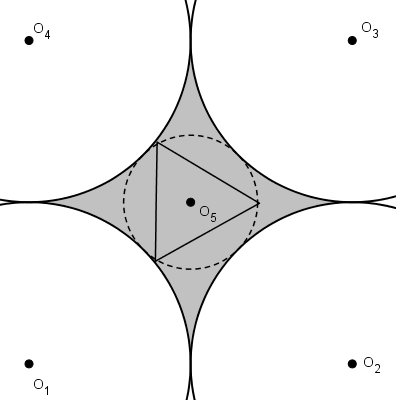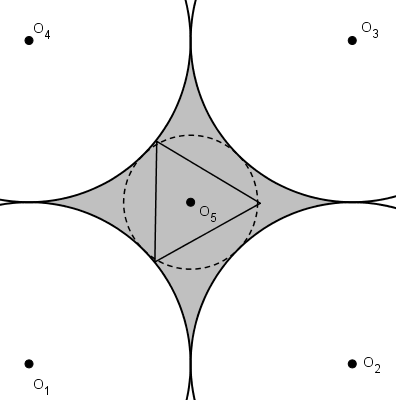
En partant de ce principe, on se rend compte qu’il n’est pas nécessaire de conserver le centre du cercle pointillé comme centre du triangle équilatéral. Il est peut-être même avantageux de déplacer le centre du triangle équilatéral.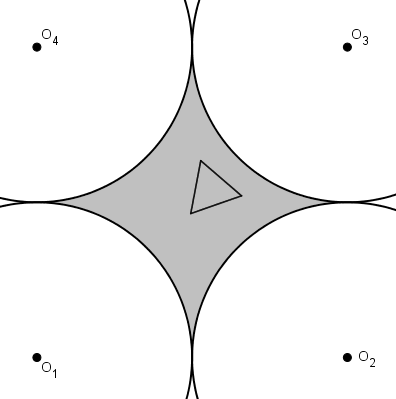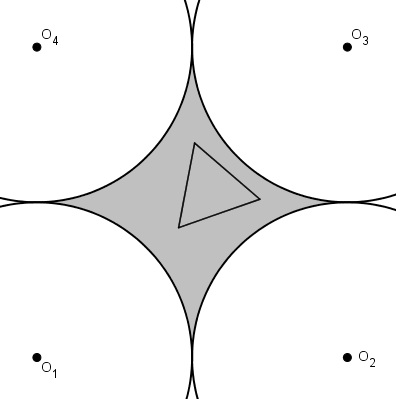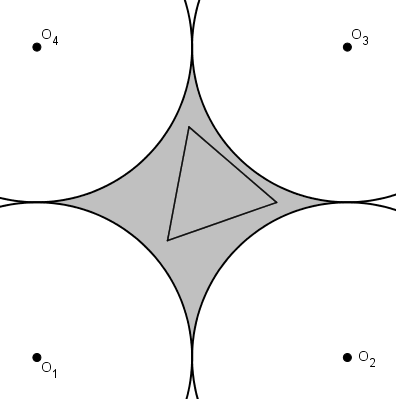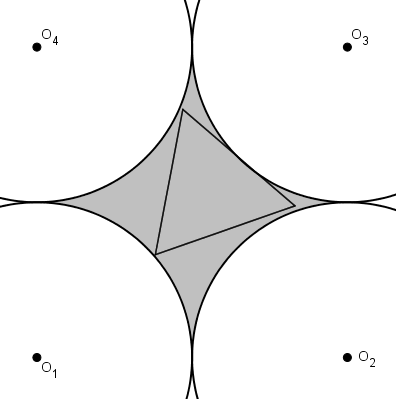

Le triangle équilatéral grossit jusqu’à ce qu’il touche un des grands cercles (par un côté tangent ou par un sommet). Pourrait-il grossir et toucher simultanément deux cercles ? Trois ? Quatre ?

Très vite on se rend compte aussi que la solution optimale sera symétrique. Il est possible que le triangle soit tangent deux cercles.

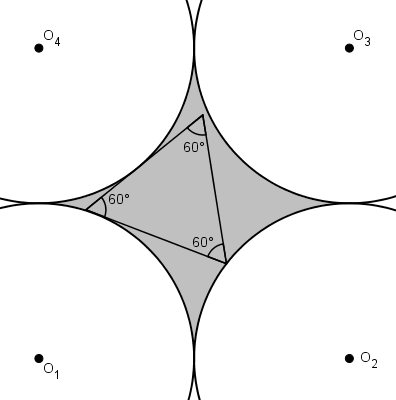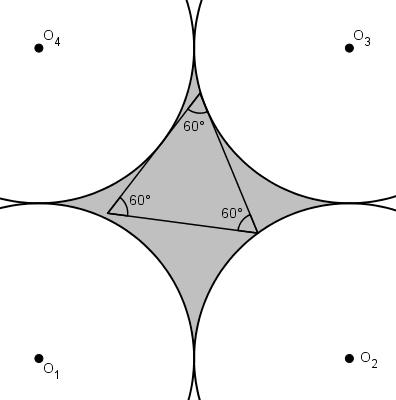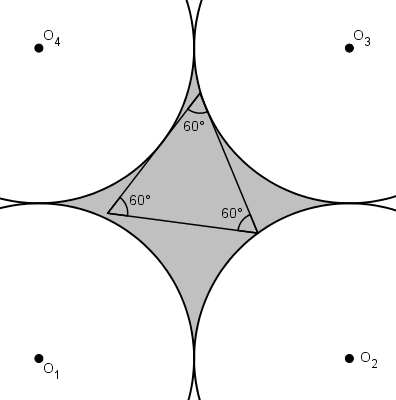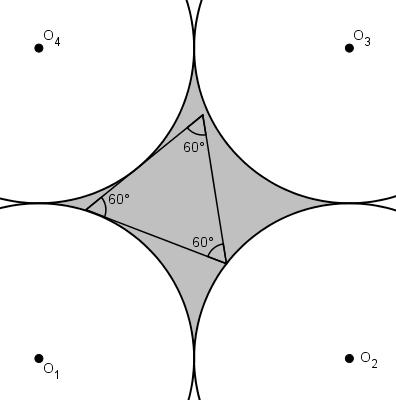
En prolongeant les tangentes, celles-ci croisent les deux autres cercles en deux autres points. En utilisant un de ces points, on peut former un triangle équilatéral.  Pour maximiser l’aire, le triangle cherché aura deux de ses sommets sur les autres cercles.

 

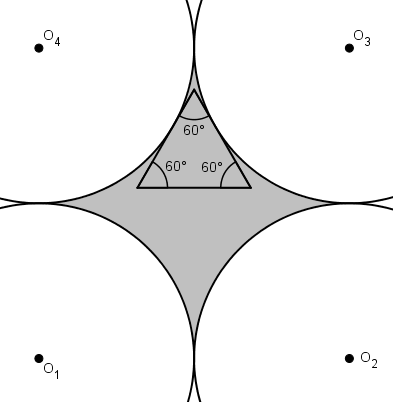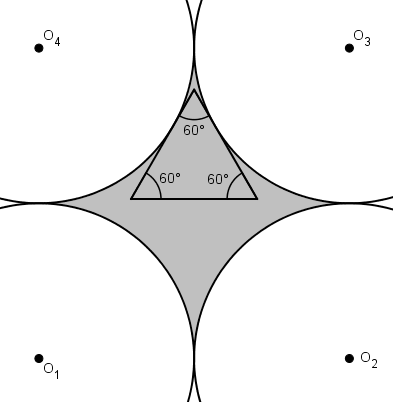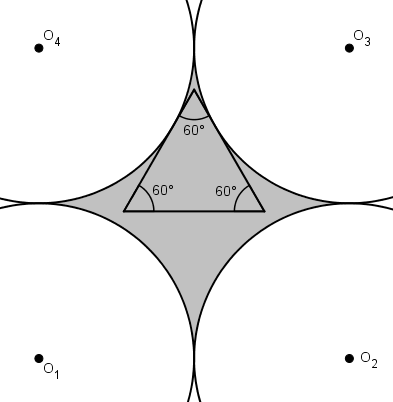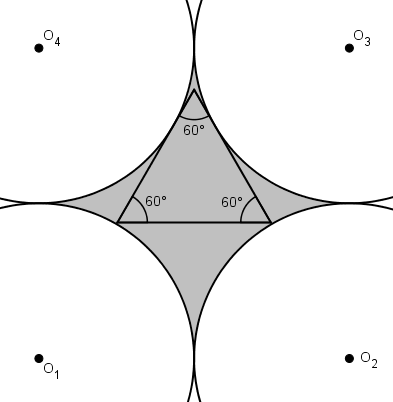
La suite

Ce n’est pas très élégant, mais plaçons le tout dans un plan cartésien, le centre $O_1$ à l’origine. Sans perdre de généralité, le triangle cherché sera tangent en $T_1$ et $T_2$ respectivement aux cercles de centre $O_4$ et de centre $O_3$ et aura deux de ses sommets en $Q$ et en $R$ respectivement sur les cercles de centre $O_1$ et de centre $O_2$. Il s’avère que les côtés du triangle tangents aux cercles du haut passent par les centres $O_1$ et $O_2$ des cercles du bas.

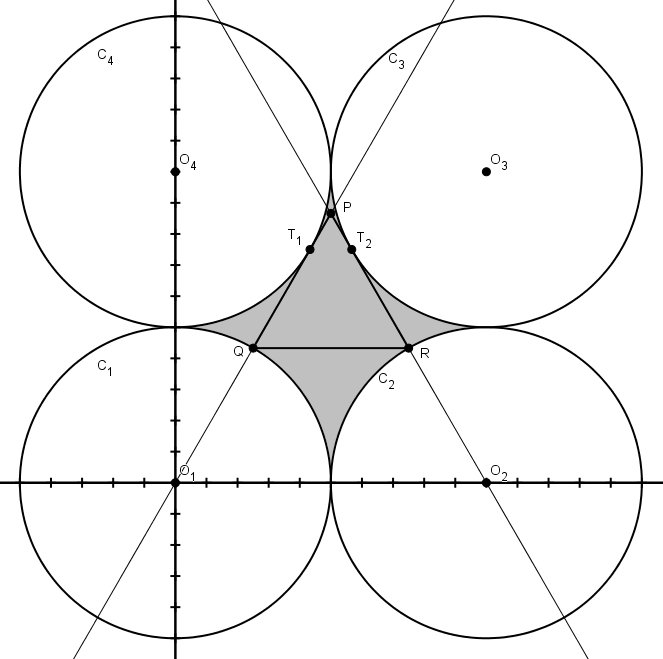
La tangente $P{T}_1$ étant perpendiculaire au rayon $O_4{T}_1$, il peut être éclairant de considérer le triangle rectangle $O_4{T}_1{O}_1$. Puisque$$m\overline{O_1{O}_4}=2m\overline{O_4{T}_1}$$on déduit que $m\mathrm{\angle }{O}_4{O}_1{T}_1={30}^{\circ }$ et donc que son complémentaire est $$m\mathrm{\angle }Q{O}_1{O}_2={60}^{\circ }$$Une démarche semblable nous donne $$m\mathrm{\angle }R{O}_2{O}_1={60}^{\circ }$$Par symétrie, le segment $QR$ étant parallèle à l’axe des abscisses, et les angles alternes-internes étant dans ce cas isométriques, $$m\mathrm{\angle }PQR=m\mathrm{\angle }PRQ={60}^{\circ }$$et on déduit que $$m\mathrm{\angle }QPR={60}^{\circ }$$car la somme des mesures des angles intérieurs d’un triangle est ${180}^{\circ }$. Le triangle équiangle est équilatéral.

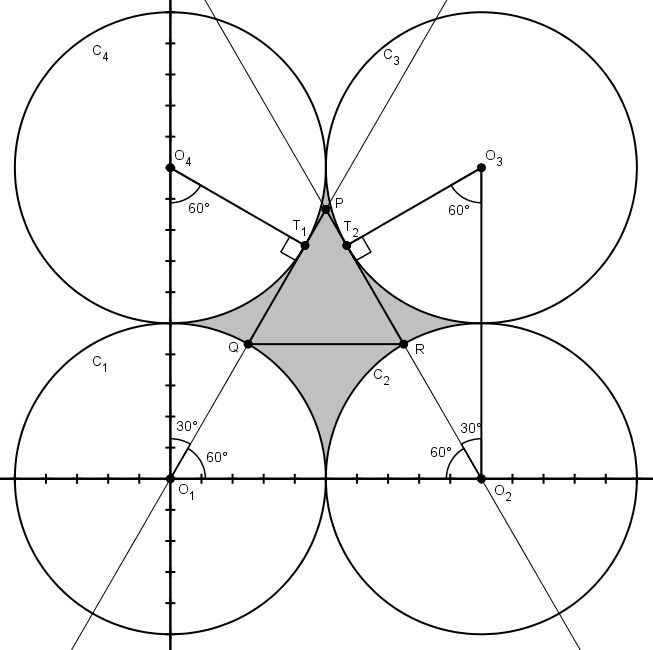
On peut emprunter ici différentes stratégies, certaines plus fines, par exemple celle des triangles semblables, car $$\mathrm{△}P{O}_1{O}_2\sim \mathrm{△}PQR$$mais je résoudrais plutôt platement un système d’équations. Sachant que $$\begin{array}{rl}\tan ({60}^{\circ })& =\frac{\sin ({60}^{\circ })}{\cos ({60}^{\circ })}\\ \\ & =\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}\\ \\ & =\frac{\frac{\sqrt{3}\times 2}{2}}{\frac{1}{2}\times 2}\\ \\ & =\sqrt{3}\end{array}$$on peut trouver l’équation de $O_{1}P$, c’est $$y=\sqrt{3}x$$car la droite passe par l’origine. L’équation de $O_{2}P$ demande un peu plus de travail car on doit déterminer son ordonnée à l’origine. La pente de la droite est $-\sqrt{3}$ et son équation est donc de la forme $$y=-\sqrt{3}x+b$$où $b$ est à déterminer. Puisque la droite passe par $O_2(10,0)$ on remplace $$0=-\sqrt{3}(10)+b$$ce qui fait $$b=10\sqrt{3}$$Son équation est donc $$y=-\sqrt{3}x+10\sqrt{3}$$

Les coordonnées de $P$ se trouvent en résolvant le système d’équations : $$\begin{array}{rl}\sqrt{3}x& =-\sqrt{3}x+10\sqrt{3}\\ \\ 2\sqrt{3}x& =10\sqrt{3}\\ \\ x& =\frac{10\sqrt{3}}{2\sqrt{3}}\\ \\ x& =5\end{array}$$L’abscisse de $P$ est $5$, ce qui, après en tenant compte de la symétrie de la figure, semble évident. L’ordonnée de $P$ est $$\begin{array}{rl}y& =\sqrt{3}(5)=-\sqrt{3}(5)+10\sqrt{5}\\ \\ & =5\sqrt{3}\end{array}$$

 

Par ailleurs, l’équation du cercle de centre $O_1$ est $$x^2+y^2=5^2$$En résolvant le système d’équations formé de l’équation du cercle et de celle de $P{T}_1$, on obtiendra les coordonnées de $Q$. En substituant $$y=\sqrt{3}x$$dans $$x^2+y^2=25$$on obtient $$x^2+{\left(\sqrt{3}x\right)}^2=25$$ce qui fait $$\begin{array}{rl}{x}^2+3x^2& =25\\ \\ 4x^2& =25\\ \\ x^2& =\frac{25}{4}\\ \\ x& =\pm \frac{5}{2}\end{array}$$Le point $Q$ étant dans le premier quadrant, on conserve la solution positive. L’ordonnée de $Q$ est $$y=\sqrt{3}\cdot \frac{5}{2}=\frac{5\sqrt{3}}{2}$$Puisque $5-\frac{5}{2}=\frac{5}{2}$, l’abscisse de $R$ sera $5+\frac{5}{2}=\frac{15}{2}$ et son ordonnée est la même que celle de $Q$, soit $\frac{5\sqrt{3}}{2}$, ce qu’on obtiendrait aussi si on avait résolu l’autre système d’équations composé de l’équation de $P{T}_2$ $$y=-\sqrt{3}x+10\sqrt{3}$$et de celle du cercle de centre $O_2$ $$(x-10{)}^2+y^2=25$$

En outre, cela implique que les côtés du triangle mesurent $5$ cm (comme les rayons des cercles, étonnant !) puisque $$m\overline{QR}=\frac{15}{2}-\frac{5}{2}=\frac{10}{2}=5$$obtenu en calculant la différence entre les abscisses de $Q$ et de $R$. La hauteur issue de $P$ est donc $$5\sqrt{3}-\frac{5\sqrt{3}}{2}=\frac{10\sqrt{3}}{2}-\frac{5\sqrt{3}}{2}=\frac{5\sqrt{3}}{2}$$obtenu en calculant la différence entre les ordonnées de $P$ et de $Q$ (ou $R$) et enfin l’aire du triangle est $$\frac{5\cdot \frac{5\sqrt{3}}{2}}{2}=\frac{25\sqrt{3}}{4}\approx 10,82$$cm².