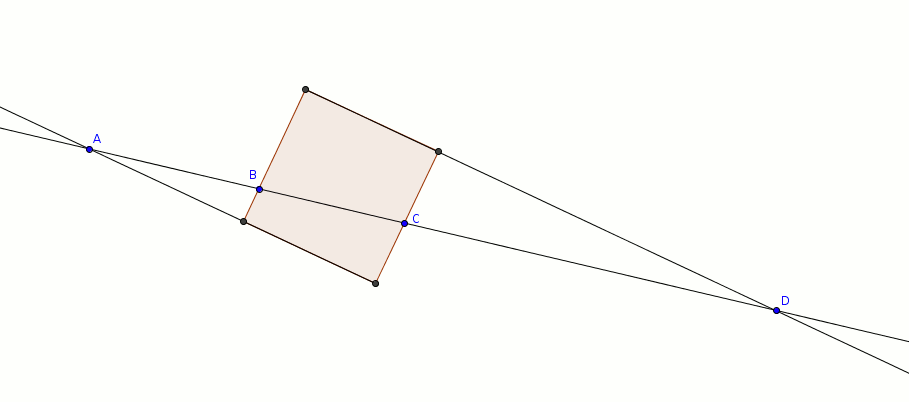
Les quatre points , , et suivants appartiennent aux quatre côtés d’un carré. Il faut reconstruire le carré à la règle et au compas.

Cela semble beaucoup plus facile que ça l’est en réalité. Avant de continuer, je vous encourage à essayer par vous-même.
Examinons premièrement deux de ces points, par exemple les points et . Un peu de géométrie élémentaire nous permet de déduire que le sommet K du carré est forcément sur le cercle de diamètre (de centre , tel qu’illustré ci-dessous).
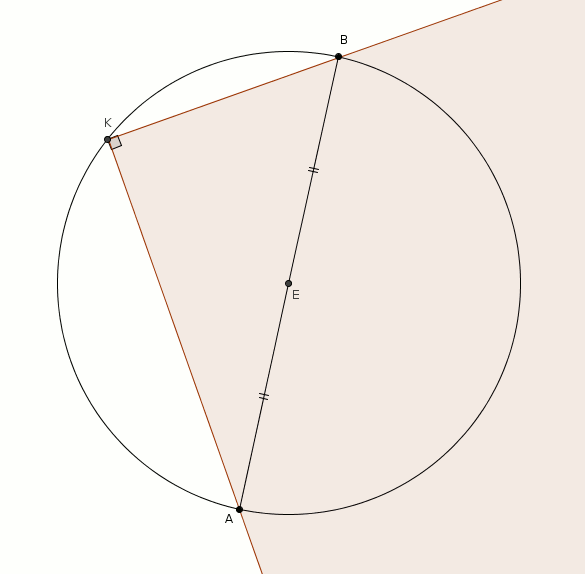
Il faut donc trouver sur ce cercle. Approfondissant notre exploration, on trace la perpendiculaire à passant par . Cette perpendiculaire coupe le cercle en (de l’autre côté de que ). Traçons .
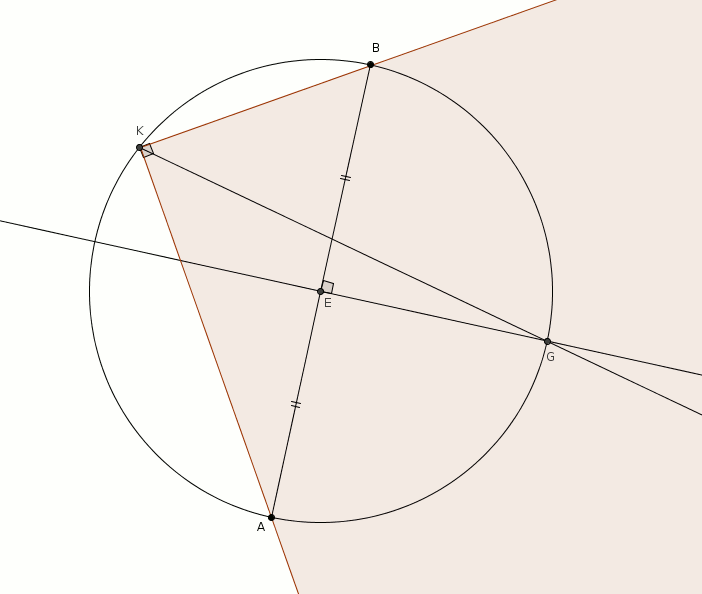
L’angle au centre et l’angle inscrit interceptent le même arc . La mesure de l’angle au centre étant , on en déduit que la mesure de l’angle inscrit est de . La même remarque s’applique aux angles au centre et inscrit . est le sommet recherché et la droite est la bissectrice de l’angle droit . La droite supporte donc la diagonale du carré.
Il ne reste qu’à appliquer ces considérations à notre figure initiale.
 À partir des quatre points initiaux, on trace les cercles de diamètre et de centre et de diamètre et de centre .
À partir des quatre points initiaux, on trace les cercles de diamètre et de centre et de diamètre et de centre .
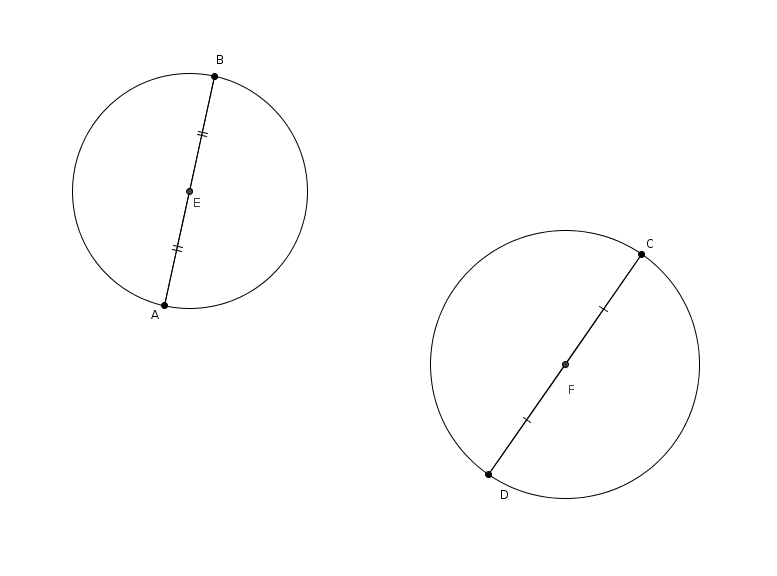 On trace ensuite les perpendiculaires à par et à par . Ces perpendiculaires coupent les cercles respectivement en et et en et (tel qu’illustré ci-dessous).
On trace ensuite les perpendiculaires à par et à par . Ces perpendiculaires coupent les cercles respectivement en et et en et (tel qu’illustré ci-dessous).
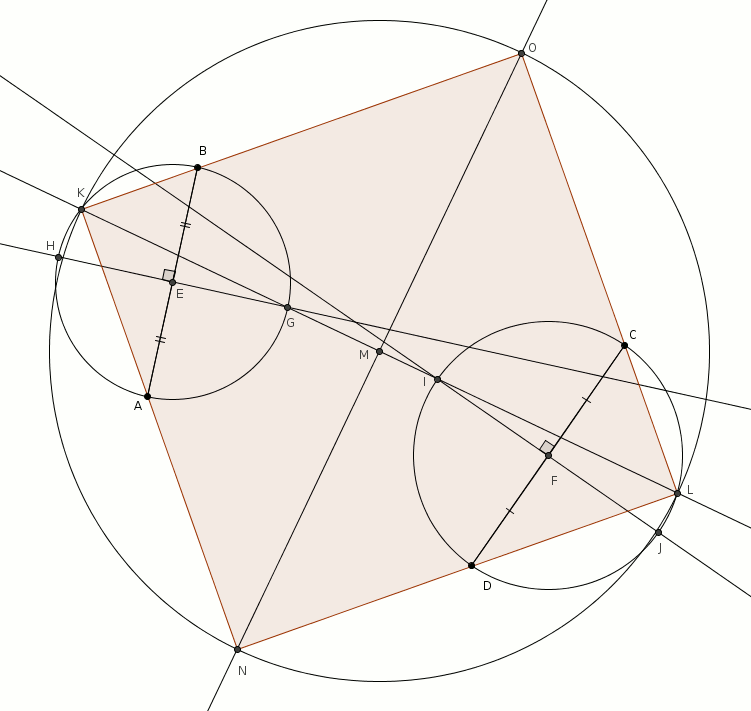
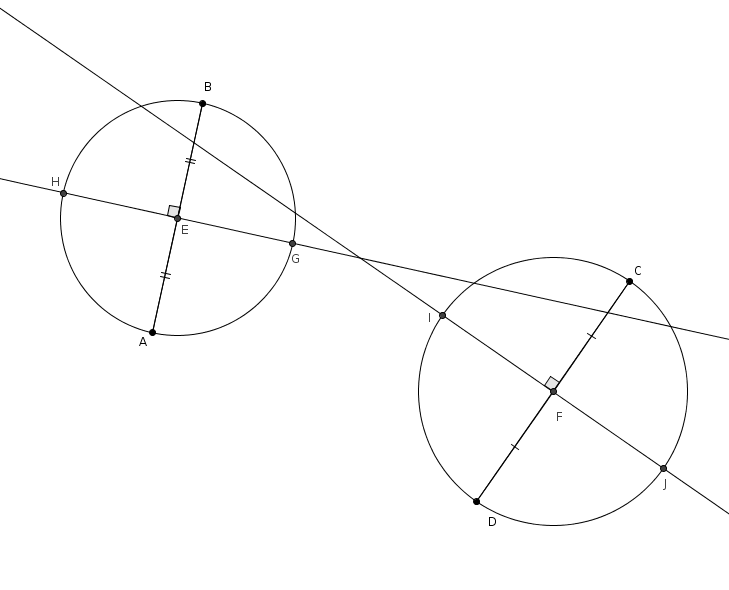 On choisit ensuite deux de ces points de telle sorte que la droite qui passe par ces points coupe les cercles à deux autres endroits. Dans notre exemple, on choisit les points et puisque la droite coupe les deux cercles à deux autres endroits, respectivement en et . Nous avons vu que la droite supportait une diagonale du carré et, dans l’autre cercle, la droite supportait aussi une diagonale du carré. L’astuce est ici de faire coïncider ces deux diagonales qui ne sont en effet qu’une seule : la droite supporte une des deux diagonales du carré… et et sont deux sommets opposés du carré.
On choisit ensuite deux de ces points de telle sorte que la droite qui passe par ces points coupe les cercles à deux autres endroits. Dans notre exemple, on choisit les points et puisque la droite coupe les deux cercles à deux autres endroits, respectivement en et . Nous avons vu que la droite supportait une diagonale du carré et, dans l’autre cercle, la droite supportait aussi une diagonale du carré. L’astuce est ici de faire coïncider ces deux diagonales qui ne sont en effet qu’une seule : la droite supporte une des deux diagonales du carré… et et sont deux sommets opposés du carré.
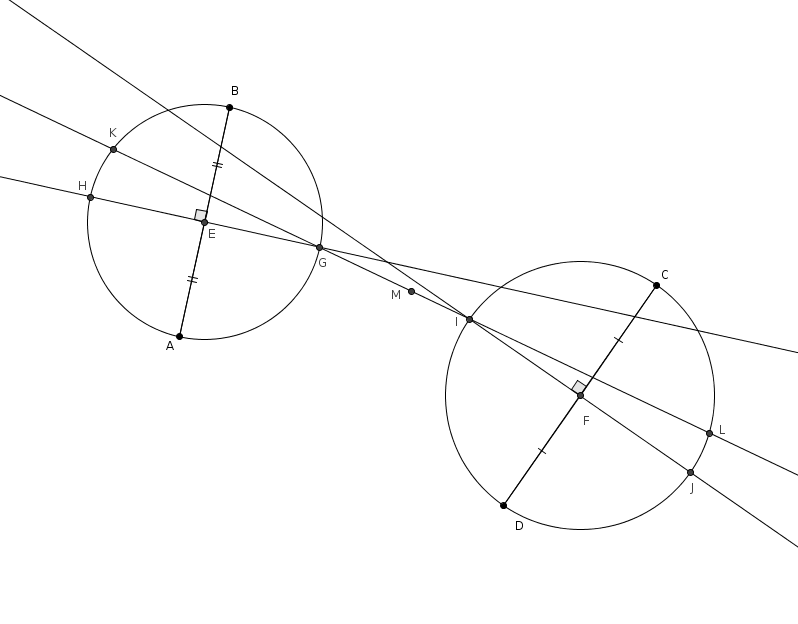
On trouve ensuite les deux autres sommets en traçant l’autre diagonale.
Voilà !
Ce qu’il y a de formidable, avec cette méthode, c’est que si l’on accepte que les points puissent se trouver sur les côtés ou sur les prolongement des côtés du carré, alors il devient toujours possible, à partir de quatre points quelconques, de reconstruire un carré. Même dans les cas les moins intuitifs… Par exemple dans le triangle ci-dessous avec le quatrième point à l’intérieur du triangle, dont voici une solution possible
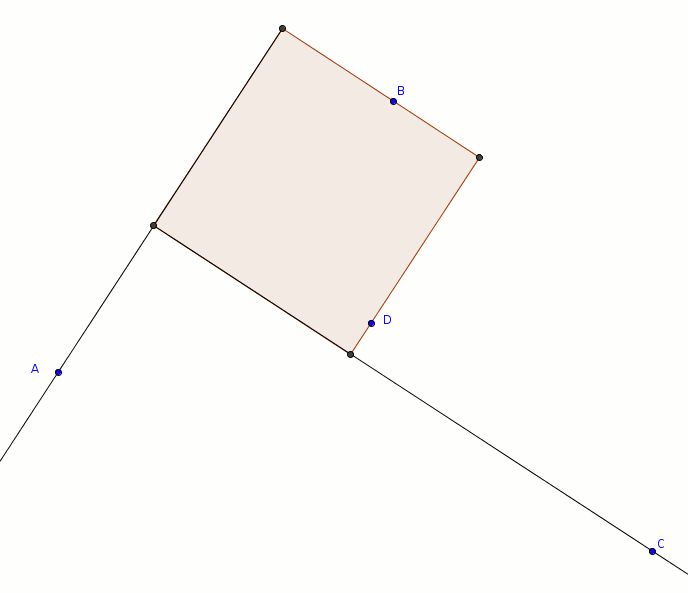 puis une autre avec les mêmes points
puis une autre avec les mêmes points
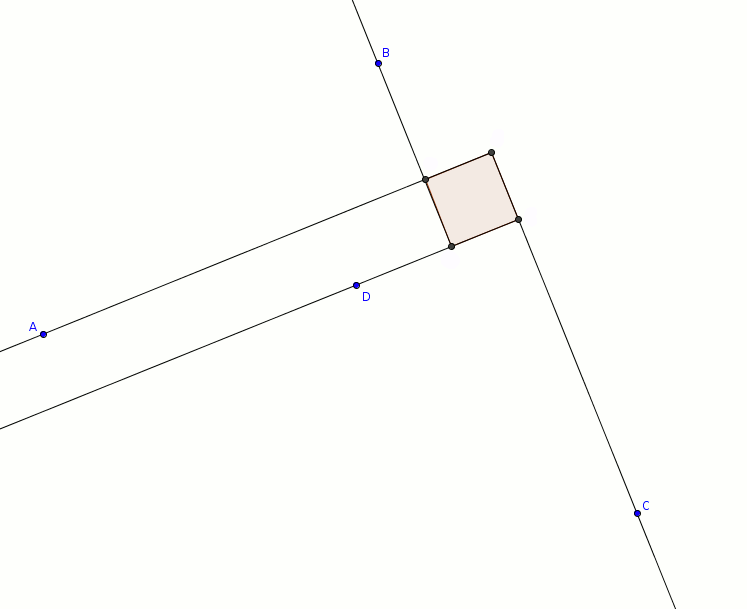 ou encore avec quatre points colinéaires !
ou encore avec quatre points colinéaires !
Inspiré par : The Oral Exam



 À partir des quatre points initiaux, on trace les cercles de diamètre
À partir des quatre points initiaux, on trace les cercles de diamètre 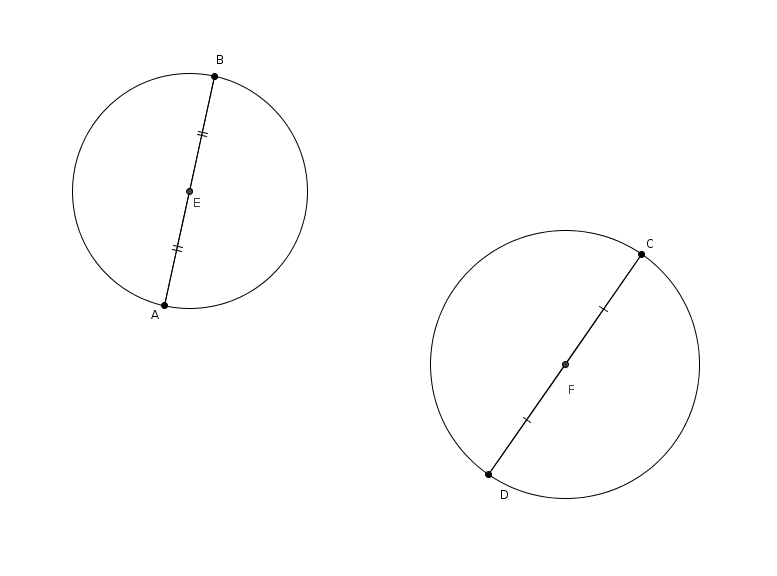 On trace ensuite les perpendiculaires à
On trace ensuite les perpendiculaires à 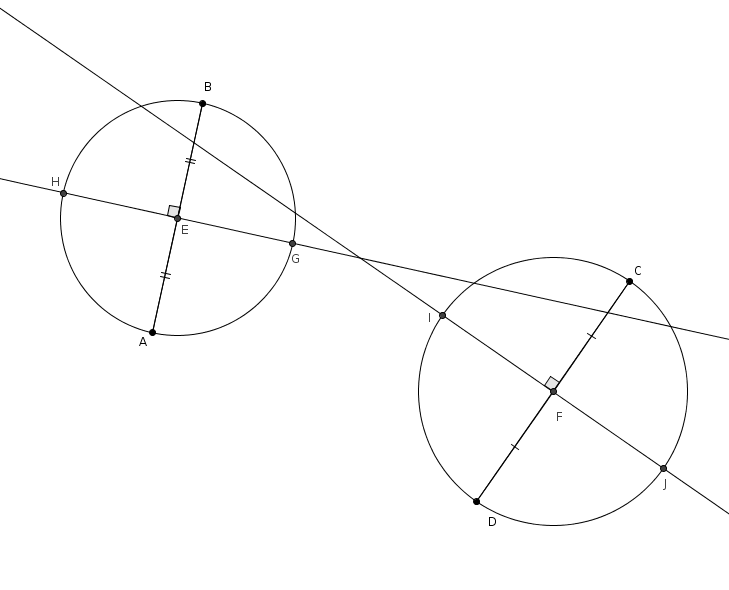 On choisit ensuite deux de ces points de telle sorte que la droite qui passe par ces points coupe les cercles à deux autres endroits. Dans notre exemple, on choisit les points
On choisit ensuite deux de ces points de telle sorte que la droite qui passe par ces points coupe les cercles à deux autres endroits. Dans notre exemple, on choisit les points 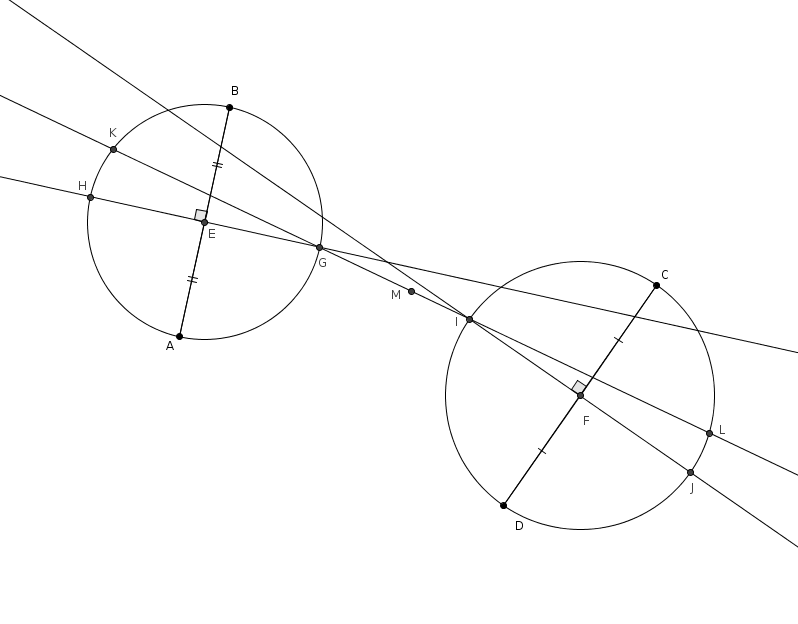

 puis une autre avec les mêmes points
puis une autre avec les mêmes points ou encore avec quatre points colinéaires !
ou encore avec quatre points colinéaires !