On considère le triangle suivant inscrit dans un cercle de rayon \(2a\). L’un des côtés du triangle étant un diamètre, le triangle est rectangle.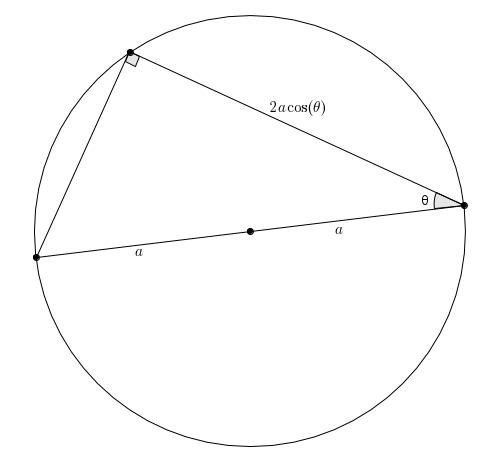
L’angle aigu \(\theta\) de ce triangle rectangle nous permet d’exprimer la longueur de la cathète adjacente à l’angle avec le cosinus. On trace ensuite un autre diamètre tel que
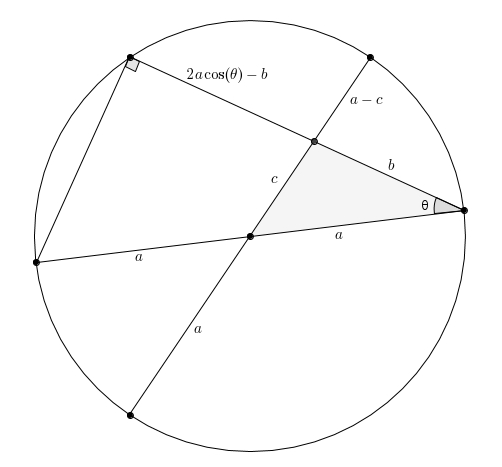Lorsque deux cordes se coupent dans un cercle, le produit des mesures des segments de l’une égale le produit des mesures des segments de l’autre. On a donc \[\left(2a\cos(\theta)-b\right)(b) = (a +c)(a-c)\]En développant, on obtient \[2ab\cos(\theta)-b^{2} = a^{2}-c^{2}\]ce qui donne… (roulement de tambour…)\[c^{2} = a^{2}+b^{2}-2ab\cos(\theta)\]la loi des cosinus (pour des angles aigus) !
Référence : Roger B. Nelson (1993), Proofs Without Words : Exercices in visual thinking