On considère deux angles non nuls
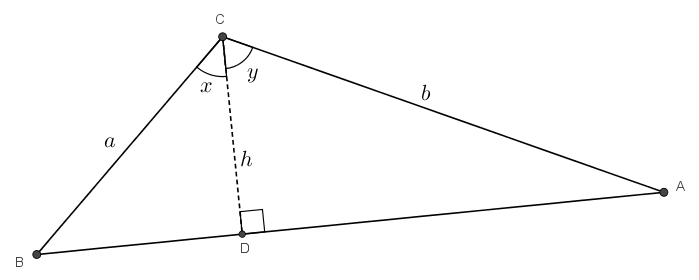
En utilisant la formule trigonométrique de l’aire du triangle, on obtient
Dans le triangle
L’astuce est de remplacer
Il ne reste qu’à diviser les deux côtés par
On considère deux angles non nuls

En utilisant la formule trigonométrique de l’aire du triangle, on obtient
Dans le triangle
L’astuce est de remplacer
Il ne reste qu’à diviser les deux côtés par