Le baseball est certainement le sport par excellence du point de vue de la statistique. Aujourd’hui dans ce billet on s’intéresse plutôt à une autre facette, disons, géométrique de ce sport. Sur la page principale du site de la ligue majeure de baseball (MLB.com), on trouve le livre des règlements officiels (tout en bas de la page, sinon en suivant ce lien).
La section 2.02 et l’Annexe 2 décrivent le marbre (home base ou home plate) et nous indiquent les dimensions qu’il doit posséder. Voici l’extrait en question :
Home Base
Home base shall be marked by a five-sided slab of whitened rubber. It shall be a 17-inch square with two of the corners removed so that one edge is 17 inches long, two adjacent sides are 8½ inches and the remaining two sides are 12 inches and set at an angle to make a point. It shall be set in the ground with the point at the intersection of the lines extending from home base to first base and to third base; with the 17-inch edge facing the pitcher’s plate, and the two 12-inch edges coinciding with the first and third base lines. […] (See drawing D in Appendix 2.)
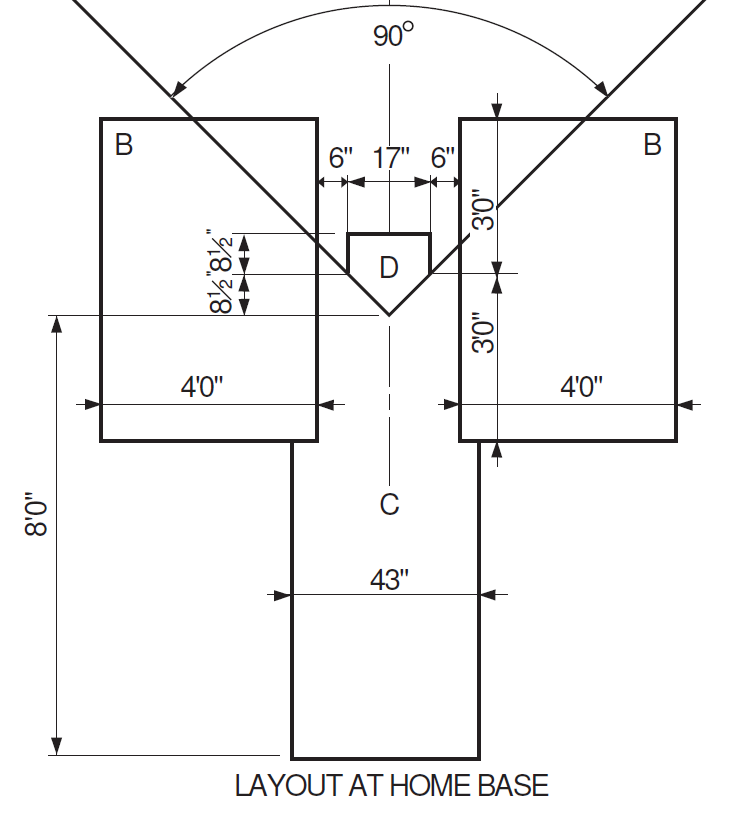
Annexe 2
C’est du sérieux. On utilise un carré de caoutchouc blanc de 17 pouces de côté duquel on retire deux coins (two corners removed) de telle sorte qu’on obtienne un pentagone possédant un côté de 17 pouces, deux côtés de 8½ pouces adjacents au côté de 17 pouces et deux côtés de 12 pouces se rejoignant en un même point et formant un angle. Un coup d’œil à l’Annexe 2 et au règlement concernant la disposition des buts et du marbre sur le terrain nous permet de déduire que cet angle est un angle droit.
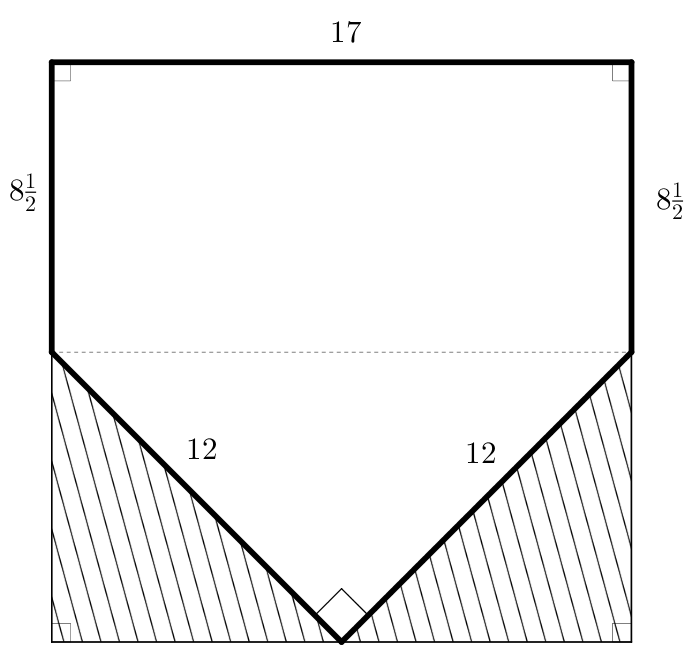
Le carré de 17 pouces et ses deux coins ôtés
En pratique, les instructions sont claires et simples, mais d’un point de vue mathématique cela cause problème. D’abord, si two corners removed suggère qu’on n’enlève que deux triangles rectangles isocèles, des triangles rectangles dont les cathètes mesurent 8½ pouces, alors c’est bien sûr inexact !\begin{align*}\sqrt{\left(8\tfrac{1}{2}\right)^{2}+ \left(8\tfrac{1}{2}\right)^{2}}&=\sqrt{\left(\frac{17}{2}\right)^{2} + \left(\frac{17}{2}\right)^{2}} \\ \\ &=\sqrt{2\left(\frac{17}{2}\right)^{2}} \\ \\ &= \frac{17\sqrt{2}}{2} \\ \\ &\approx 12,\!02\end{align*}Cela produit des côtés dont la mesure est légèrement supérieure à 12 pouces. Oups ! On doit donc enlever un peu plus que deux triangles rectangles ; en d’autres mots, l’intersection des deux côtés de 12 pouces ne coïncide pas avec le côté du carré, elle est légèrement en retrait. Soit.
Supposons qu’on ait bien des côtés de 12 pouces, le règlement suggère alors qu’il existe un triangle rectangle isocèle dont les cathètes mesurent 12 pouces et l’hypoténuse 17 pouces. Hélas ! C’est encore bien sûr impossible. \begin{align*}\sqrt{12^{2}+12^{2}} &= \sqrt{2 \cdot 12^2} \\ \\ &= 12\sqrt{2} \\ \\ &\approx 16,\!97\end{align*}Une valeur légèrement inférieure à 17 pouces. Si près mais si loin en même temps ! Un tel marbre ne peut exister. Scandale !
Un marbre pentagonal qui aurait des côtés de 8½, 17, 8½, 12 et 12 contiendrait un angle \(\theta\) de \begin{align*}17^{2} &= 12^{2}+12^{2}-2(12)(12)\cos(\theta) \\ \\ 289 &= 144 + 144-288\cos(\theta) \\ \\ \cos(\theta) &= -\frac{1}{288} \\ \\ \theta &\approx 90,\!2^{\circ}\end{align*}
Référence :
Office of the Commissioner of Baseball, OFFICIAL BASEBALL RULES, 2023 Edition
Alsina, Claudi et Roger B. Nelsen, A Panoply of Polygons, AMS|MAA Press, 2023