La relation de Pythagore nous dit que dans un triangle rectangle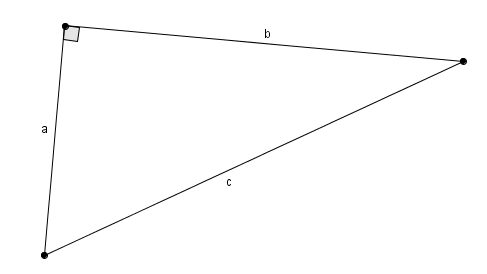
on a \[a^{2}+ b^{2} = c^{2}\]Les résultats du dernier billet, celui sur l’équation de Fermat, nous permet donc de trouver les dimensions de triangles rectangles dont les trois côtés sont des nombres entiers. Il est possible d’établir un autre lien fort intéressant de la même nature.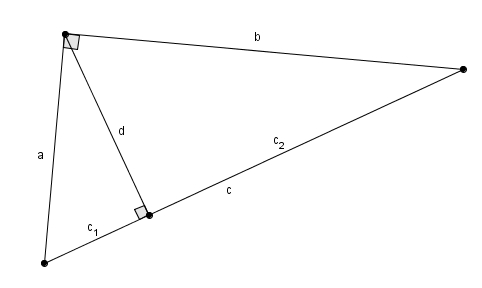
En traçant la hauteur issue de l’angle droit (ou relative à l’hypoténuse), le segment \(d\) sur la figure, on crée des triangles semblables. En considérant le grand triangle rectangle initial et un des deux plus petits triangles rectangles semblables, il nous est possible d’établir cette proportion \[\frac{c}{d} = \frac{b}{d}\]ou de manière équivalente \[c = \frac{ab}{d}\]En élevant au carré on obtient \[c^{2} = \frac{a^{2}b^{2}}{d^{2}}\]ce qui nous permet de remplacer dans l’équation initiale\[a^{2} + b^{2} = \frac{a^{2}b^{2}}{d^{2}}\]En divisant par \(a^{2}b^{2}\) on obtient \[\frac{a^{2}}{a^{2}b^{2}} + \frac{b^{2}}{a^{2}b^{2}}=\frac{1}{d^{2}}\]ce qui fait après simplifications \[\frac{1}{a^{2}} + \frac{1}{b^{2}} = \frac{1}{d^{2}}\]C’est l’équation du dernier billet lorsque l’exposant vaut \(-2\). On pose donc \[a = 2pq\left(p^{2}+q^{2}\right), \quad b=\left(p^{2}+q^{2}\right)\left(p^{2}-q^{2}\right), \quad d = 2pq\left(p^{2}-q^{2}\right)\]avec \(p\) et \(q\) deux entiers premiers entre eux et de parité différente, et \(p>q\). Comme\[c = \frac{ab}{d}\]on a bien \[c=\frac{2pq\left(p^{2}+q^{2}\right) \cdot \left(p^{2}+q^{2}\right)\left(p^{2}-q^{2}\right)}{2pq\left(p^{2}-q^{2}\right)} = \left(p^{2}+q^{2}\right)^{2}\]et \(c\) est un entier ! On peut même trouver que la mesure des segments sur l’hypoténuse déterminés par la hauteur (\(c_1\) et \(c_2\) sur la figure) sont elles aussi entières. Par Pythagore, on a \begin{align*}\left(c_{1}\right)^{2}+d^{2} &= a^{2} \\ \\ \left(c_{1}\right)^{2} + \left(2pq\left(p^{2}-q^{2}\right)\right)^{2} &=\left(2pq\left(p^{2}+q^{2}\right)\right)^{2} \\ \\ \left(c_{1}\right)^{2} &= \left(2pq\left(p^{2}+q^{2}\right)\right)^{2}-\left(2pq\left(p^{2}-q^{2}\right)\right)^{2}\end{align*}et en effectuant une mise en évidence simple puis en factorisant la différence de carrés, on trouve\begin{align*}\left(c_{1}\right)^{2} &=\left(2pq\left(p^{2}+q^{2}\right)\right)^{2}-\left(2pq\left(p^{2}-q^{2}\right)\right)^{2} \\ \\ &=4p^{2}q^{2}\left(\left(p^{2}+q^{2}\right)^{2}-\left(p^{2}-q^{2}\right)^{2}\right) \\ \\ &= 4p^{2}q^{2}\left(p^{2}+q^{2}+\left(p^{2}-q^{2}\right)\right)\left(p^{2}+q^{2}-\left(p^{2}-q^{2}\right)\right) \\ \\ &= 4p^{2}q^{2}\left(2p^{2}\right)\left(2q^{2}\right) \\ \\ &= \left(4p^{2}q^{2}\right)^{2}\end{align*}c’est-à-dire\[c_{1}=4p^{2}q^{2}\]un nombre entier ! Puis la même chose avec \begin{align*}\left(c_{2}\right)^{2} + d^{2} &=b^{2} \\ \\ \left(c_{2}\right)^{2} + \left(2pq\left(p^{2}-q^{2}\right)\right)^{2}&=\left(\left(p^{2}+q^{2}\right)\left(p^{2}-q^{2}\right)\right)^{2} \\ \\ \left(c_{2}\right)^{2}&=\left(\left(p^{2}+q^{2}\right)\left(p^{2}-q^{2}\right)\right)^{2}-\left(2pq\left(p^{2}-q^{2}\right)\right)^{2}\end{align*}et encore une fois après une mise en évidence simple et une factorisation d’une différence de carrés, on a \begin{align*}\left(c_{2}\right)^{2}&=\left(\left(p^{2}+q^{2}\right)\left(p^{2}-q^{2}\right)\right)^{2}-\left(2pq\left(p^{2}-q^{2}\right)\right)^{2} \\ \\ &=\left(p^{2}-q^{2}\right)^{2}\left(\left(p^{2}+q^{2}\right)^{2}-\left(2pq\right)^{2}\right) \\ \\ &=\left(p^{2}-q^{2}\right)^{2}\left(p^{2}+q^{2}+2pq\right)\left(p^{2}+q^{2}-2pq\right) \\ \\ &=\left(p^{2}-q^{2}\right)^{2}\left(p+q\right)^{2}\left(p-q\right)^{2}\end{align*}c’est-à-dire \begin{align*}c_{2}&=\left(p^{2}-q^{2}\right)\left(p+q\right)\left(p-q\right) \\ \\ &=\left(p^{2}-q^{2}\right)\left(p^{2}-q^{2}\right)\end{align*}encore un nombre entier ! Pourquoi arrêter le plaisir ? On peut même vérifier que \begin{align*}c_{1}+c_{2} &= 4p^{2}q^{2}+\left(p^{2}-q^{2}\right)^{2} \\ \\ &=4p^{2}q^{2}+p^{4}-2p^{2}q^{2}+q^{4} \\ \\ &=p^{4}+2p^{2}q^{2}+q^{4} \\ \\ &= \left(p^{2}+q^{2}\right)^{2} \\ \\ &=c\end{align*}Tout fonctionne ! C’est un truc pratique pour tout enseignant voulant que les solutions à son exercice sur les relations métriques dans le triangle rectangle soient « arrangées avec le gars des vues ».