Sur les cotangentes de trois angles complémentaires

On considère un triangle et son cercle inscrit.

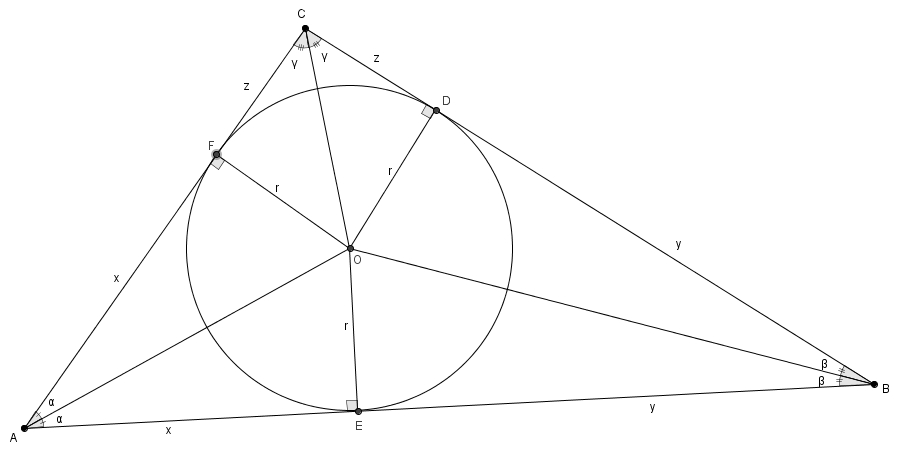
Le centre du cercle est bien sûr l’intersection des bissectrices.  On retrouve dans cette figure trois paires de triangles rectangles isométriques.  On s’intéresse à un triangle de chaque paire.

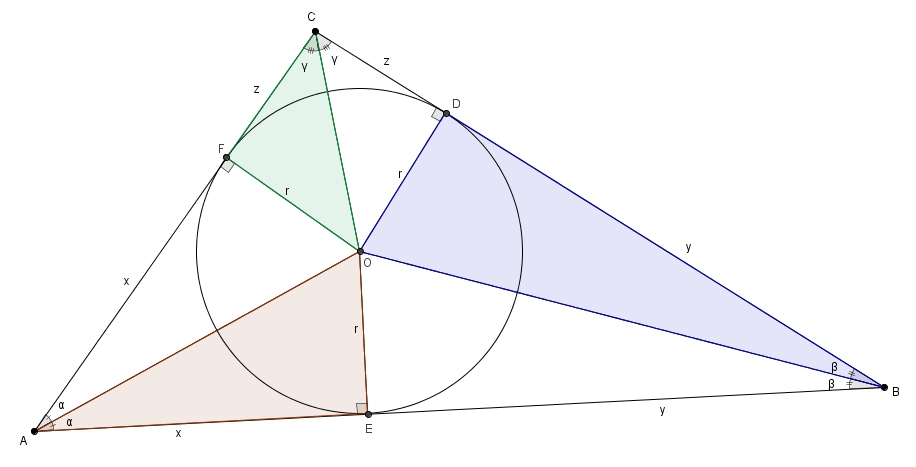
On utilise aussi le fait que $$\alpha +\beta +\gamma =\frac{\pi }{2}$$On choisit en premier lieu un triangle semblable au triangle $AEO$ et dont le rapport de similitude est $yz$.

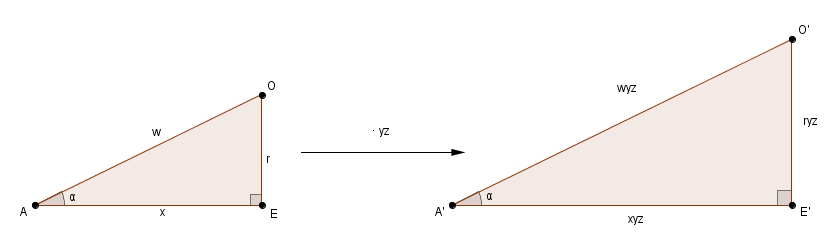
où $$w=\sqrt{r^2+x^2}$$On choisit ensuite un triangle semblable au triangle bleu $BDO$.  La cathète adjacente à l’angle $\beta$ étant $y$, on choisit le rapport de similitude comme étant $wz$

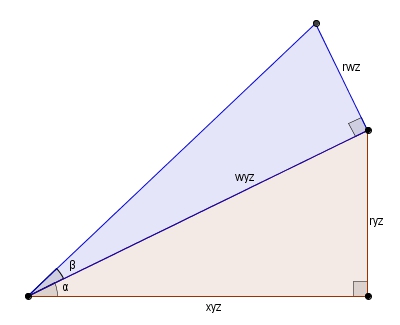
Bien sûr, puisque $$\alpha +\beta +\gamma =\frac{\pi }{2}$$un triangle semblable au triangle vert $CFO$ viendra compléter l’angle droit.  Nous n’avons pas pour le moment le rapport de similitude de ce triangle vert.

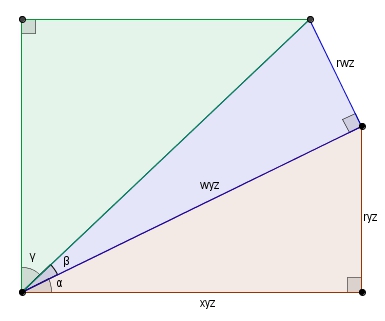
En complétant le rectangle, on remarque que le petit triangle rectangle dont l’hypoténuse est $rwz$ possède un angle $\alpha$. Il est donc semblable au triangle $AEO$. Puisque l’hypoténuse de $AEO$ est $w$, le rapport de similitude est $rz$.

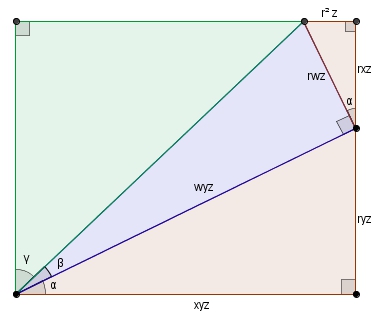
Comme les côtés opposés d’un rectangle sont isométriques, cela implique que la cathète adjacente à l’angle γ dans le triangle vert est $$rxz+ryz=rz(x+y)$$et que le rapport de similitude recherché est donc $r(x+y)$.  On a

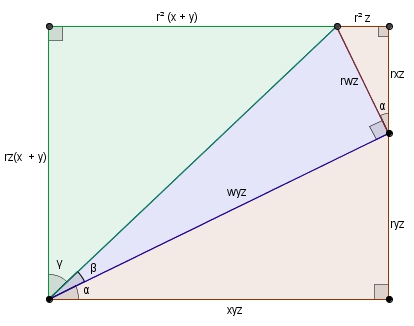
duquel on tire cette jolie égalité $$xyz=r^2(x+y)+r^{2}z$$ou $$xyz=r^2(x+y+z)$$Enfin, en divisant par $r^3$ de chaque côté, on obtient $$\frac{x}{r}\cdot \frac{y}{r}\cdot \frac{z}{r}=\frac{x}{r}+\frac{y}{r}+\frac{z}{r}$$c’est-à-dire que pour $$\alpha +\beta +\gamma =\frac{\pi }{2}$$on a $$\cot (\alpha )\cdot \cot (\beta )\cdot \cot (\gamma )=\cot (\alpha )+\cot (\beta )+\cot (\gamma )$$

Référence : Roger B. Nelsen (2008), Mathematics Magazine Vol. 81, pp. 58-61