Test pour nombres polygonaux

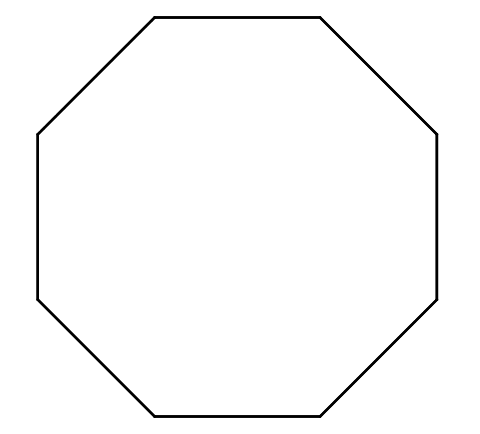
Je viens de voir avec mes élèves de première secondaire comment trouver la somme des mesures des angles intérieurs d’un polygone. Si le polygone est convexe, c’est facile de choisir un sommet et de tracer toutes les diagonales issues de ce sommet (si le polygone est concave c’est plus délicat, il faut tracer des diagonales de plus d’un sommet qui ne se coupent pas).

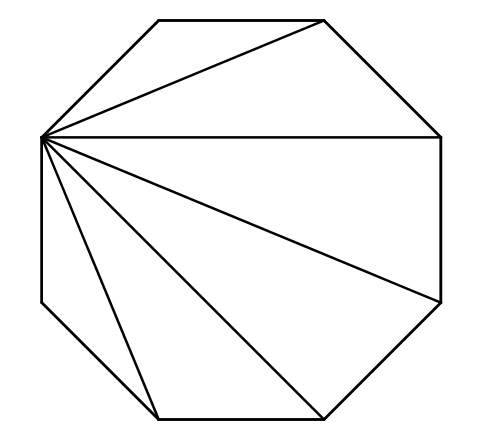
Les diagonales divisent le polygone en triangles. Puisqu’on ne peut relier un sommet à lui-même ni aux deux sommets qui lui sont adjacents, dans un polygone à $n$ côtés, il y a $n-3$ diagonales qui divisent le polygone en $n-2$ triangles.

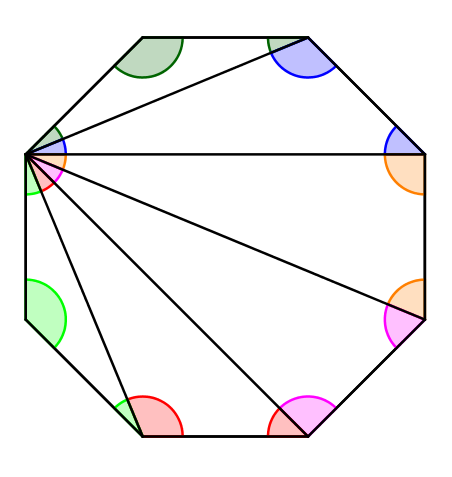
Sachant que la somme des mesures des angles intérieurs d’un triangle est 180°, on réussit à trouver ce qu’on cherche facilement :

$$\underset{n-2\text{ fois}}{\underbrace{{180}^{\circ }+{180}^{\circ }+{180}^{\circ }+\dots +{180}^{\circ }}}$$

La somme des mesures des angles d’un polygone à $n$ côtés est $(n-2)\times {180}^{\circ }$.

Cela m’a fait penser à cette petite astuce dans laquelle on considère les diagonales d’un polygone et les nombres polygonaux. Un nombre polygonal est un nombre qu’on peut représenter avec des points disposés en forme de polygone régulier. Les premiers nombres polygonaux qui nous intéressent sont les nombres triangulaires.

Les nombres triangulaires

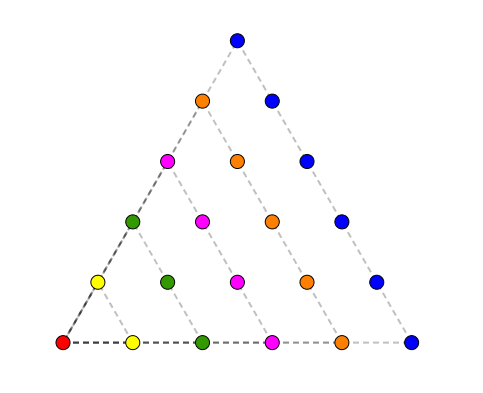
Les nombres triangulaires sont, sans surprise, les nombres qu’on peut représenter avec un triangle. Les nombres triangulaires sont $$1,3,6,10,15,21,28,36,\dots$$

Le $n^{\text{e}}$ nombre triangulaire correspond à la somme des $n$ premiers entiers. Par exemple, le sixième nombre triangulaire est la somme des six premiers entiers $$t_6=1+2+3+4+5+6=21$$On connaît l’histoire, que dis-je, la légende, d’un jeune Gauss qui réussit à calculer de manière très astucieuse la somme des $n$ premiers entiers. L’expression qui correspond à la somme des $n$ premiers entiers est donc aussi celle qui génère les nombres triangulaires. Si $t_n$ représente le $n^{\text{e}}$ nombre triangulaire, alors $$t_n=\frac{n(n+1)}{2}$$

Les autres nombres polygonaux

On s’intéresse ensuite aux autres nombres polygonaux. Dans l’ordre, on retrouverait les nombres carrés.

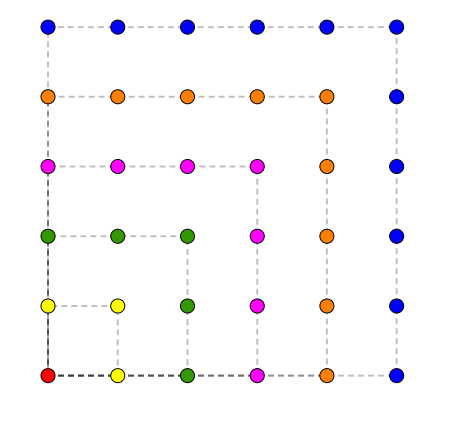
Dans ce cas-ci, on obtient donc la somme des nombres impairs.

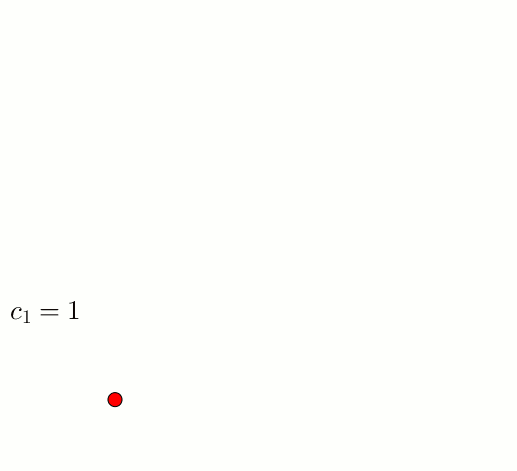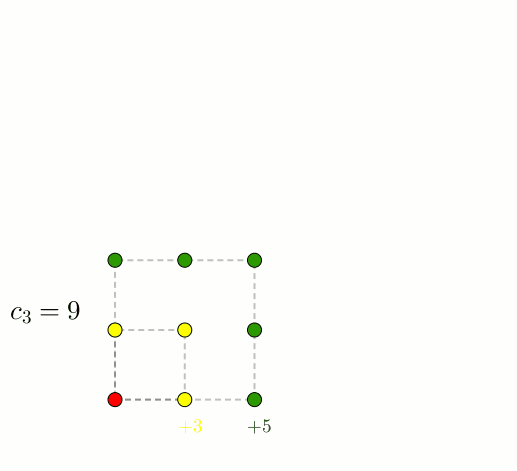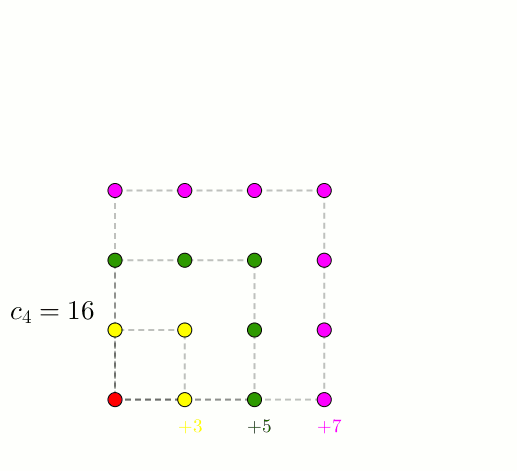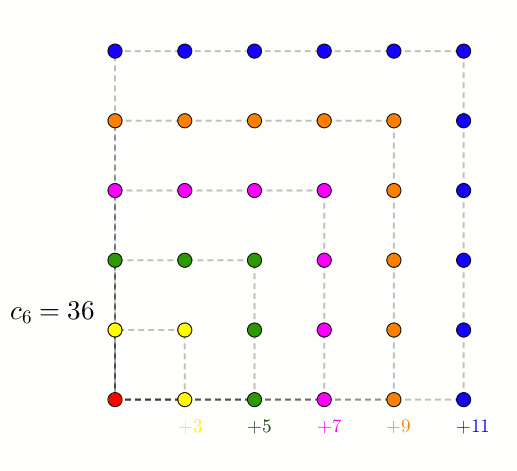
Évidemment, on a $$c_n=n^2$$

Suivent les nombres pentagonaux.

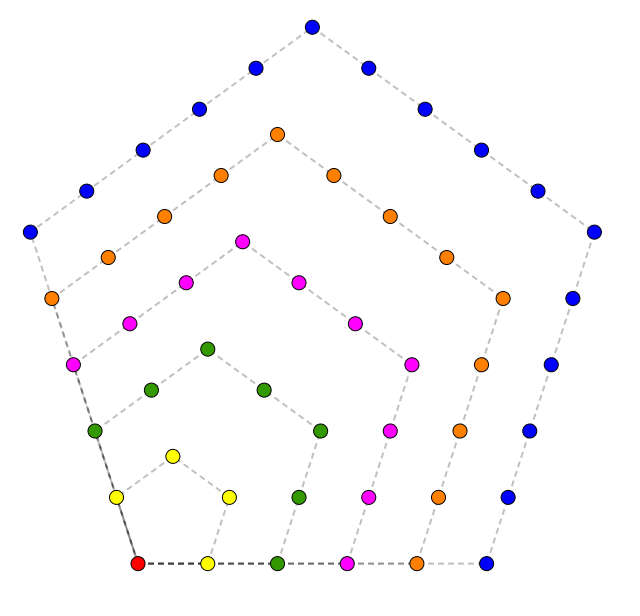
L’expression du $n^{\text{e}}$ nombre pentagonal est $$p_n=\frac{3n^2-n}{2}$$

Puisqu’il faut bien s’arrêter quelque part, on termine avec les nombres hexagonaux.

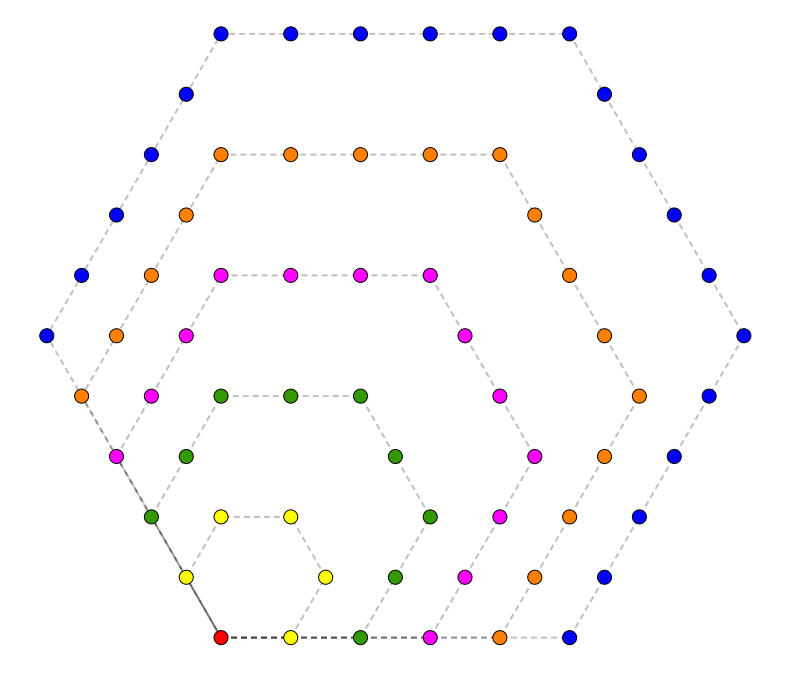
Dans ce cas-ci, c’est $$h_n=2n^2-n$$qui nous donne le $n^{\text{e}}$ nombre hexagonal.

On constate que les règles qui nous donnent le $n^{\text{e}}$ nombre polygonal sont toutes quadratiques. Ce n’est pas surprenant car les nombres polygonaux sont tous des sommes de nombres en progression arithmétique.

• Le $n^{\text{e}}$ nombre triangulaire est la somme des $n$ premiers termes de la suite arithmétique de premier terme $1$ et de raison $1$.
• Le $n^{\text{e}}$ nombre carré est la somme des $n$ premiers termes de la suite arithmétique de premier terme $1$ et de raison $2$.
• Le $n^{\text{e}}$ nombre pentagonal est la somme des $n$ premiers termes de la suite arithmétique de premier terme $1$ et de raison $3$.
• Le $n^{\text{e}}$ nombre hexagonal est la somme des $n$ premiers termes de la suite arithmétique de premier terme $1$ et de raison $4$.
• En général, le $n^{\text{e}}$ nombre $k-$gonal est la somme des $n$ premiers termes de la suite arithmétique de premier terme $1$ et de raison $k-2$.

Si ${\pi }_{(k,n)}$ est le $n^{\text{e}}$ nombre $k-$gonal, alors $${\pi }_{(k,n)}=\sum _{i=0}^{n-1}1+(k-2)i$$

	1	2	3	4	5	6	7	8	9
Nombres triangulaires	1	3	6	10	15	21	28	36	45
Nombres carrés	1	4	9	16	25	36	49	64	81
Nombres pentagonaux	1	5	12	22	35	51	70	92	117
Nombres hexagonaux	1	6	15	28	45	66	91	120	120
Nombres heptagonaux	1	7	18	34	55	81	112	148	189
Nombres octogonaux	1	8	21	40	65	96	133	176	225

 

Les diagonales (bis)

Qu’obtient-on lorsqu’on trace les diagonales issues d’un sommet dans ces polygones ? Des triangles, bien sûr ! Cela nous permet de découvrir une jolie relation qui lie les nombres polygonaux aux nombres triangulaires. Cette relation génère les formules trouvées ci-haut et, avec quelques manipulations algébriques supplémentaires, un test pour savoir si un nombre est $k-$gonal ou non.

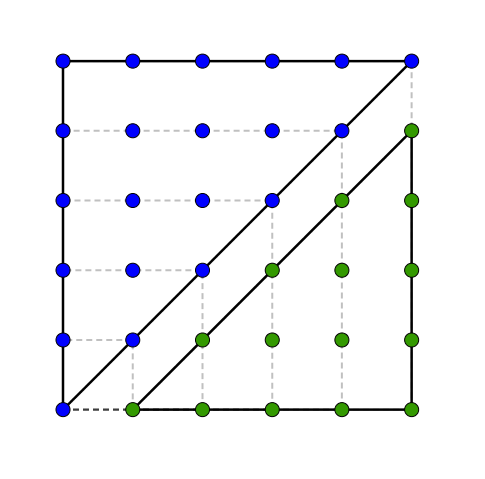
Puisqu’il sera possible d’obtenir deux triangles en traçant la diagonale issue d’un sommet dans un carré, un moment suffit pour nous convaincre que $$c_n=t_n+t_{n-1}$$De manière analogue, on constate que dans le pentagone, on obtiendra trois triangles et que $$p_n=t_n+2t_{n-1}$$

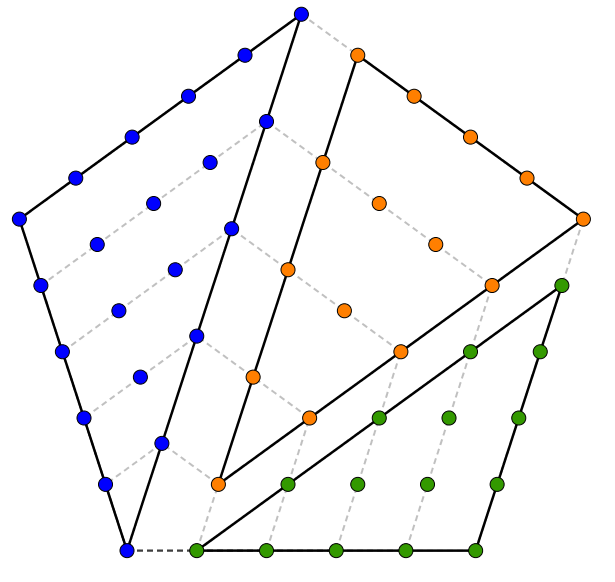
Enfin, le cas de l’hexagone, avec ses quatre triangles,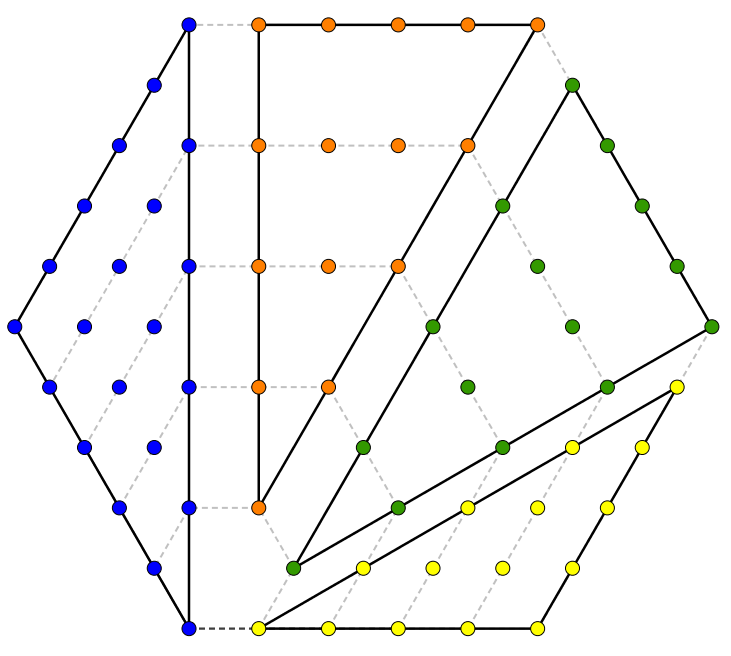

nous permet d’obtenir $$h_n=t_n+3t_{n-1}$$Puisque le $k-$gone se divisera en $k-2$ triangles, on trouve $${\pi }_{(k,n)}=t_n+(k-3)t_{n-1}$$c’est-à-dire un triangle de $t_n$ et $k-3$ triangles de $t_{n-1}$ ce qui fait $k-2$ triangles au total. En se rappelant que $$t_n=\frac{n(n+1)}{2}$$la relation précédente nous permet de trouver une expression générale pour le $n^{\text{e}}$ nombre $k-$gonal.$$\begin{array}{rl}{\pi }_{(k,n)}& =t_n+(k-3)t_{n-1}\\ \\ & =\frac{n(n+1)}{2}+(k-3)\frac{(n-1)(n)}{2}\\ \\ & =\frac{n^2+n}{2}+(k-3)\frac{n^2-n}{2}\\ \\ & =\frac{n^2+n+(k-3)(n^2-n)}{2}\\ \\ & =\frac{n^2+n+k{n}^2-3n^2-kn+3n}{2}\\ \\ & =\frac{(k-2)n^2-(k-4)n}{2}\end{array}$$

Ainsi, si $k=4$, on obtient $$\begin{array}{rl}{\pi }_{(4,n)}& =\frac{(4-2)n^2-(4-4)n}{2}\\ \\ & =\frac{2n^2+(0)n}{2}\\ \\ & =\frac{2n^2}{2}\\ \\ & =n^2\\ \\ & =c_n\end{array}$$

Si $k=5$, on a $$\begin{array}{rl}{\pi }_{(5,n)}& =\frac{(5-2)n^2-(5-4)n}{2}\\ \\ & =\frac{3n^2-n}{2}\\ \\ & =p_n\end{array}$$

Enfin, si $k=6$, $$\begin{array}{rl}{\pi }_{(6,n)}& =\frac{(6-2)n^2-(6-4)n}{2}\\ \\ & =\frac{4n^2-2n}{2}\\ \\ & =2n^2-n\\ \\ & =h_n\end{array}$$ce qu’on avait plus tôt !

 

Le test pour nombres polygonaux

L’expression précédente peut servir de test. Par exemple, le nombre $341$ est-il un nombre octogonal ? On pose $k=8$ et ${\pi }_{(8,n)}=341$ : $$\begin{array}{rl}341& =\frac{(8-2)n^2-(8-4)n}{2}\\ \\ 341& =\frac{6n^2-4n}{2}\\ \\ 341& =3n^2-2n\\ \\ 0& =3n^2-2n-341\\ \\ 0& =3n^2-33n+31n-341\\ \\ 0& =3n(n-11)+31(n-11)\\ \\ 0& =(n-11)(3n+31)\end{array}$$En ignorant la deuxième solution, $n=-\frac{31}{3}$, et en conservant $n=11$, on trouve qu’effectivement, $341$ est le ${11}^{\text{e}}$ nombre octogonal.

Le nombre $219$ est-il un nombre heptagonal ? On pose $k=7$ et ${\pi }_{(7,n)}=219$ : $$\begin{array}{rl}219& =\frac{(7-2)n^2-(7-4)n}{2}\\ \\ 219& =\frac{5n^2-3n}{2}\\ \\ 438& =5n^2–3n\\ \\ 0& =5n^2-3n-438\end{array}$$Ici, on ne peut factoriser aisément. Le calcul du discriminant nous donne $$\begin{array}{rl}\mathrm{\Delta }& =(-3{)}^2–4(5)(-438)\\ \\ & =8769\end{array}$$Puisque $8769>8649={93}^2$ et $8769<8836={94}^2$, le discriminant n’est pas un carré et les solutions sont irrationnelles. Conclusion : le nombre $219$ n’est pas une nombre heptagonal.

Il faut donc résoudre une équation quadratique chaque fois. Et si jamais elle est difficilement factorisable avec la méthode somme-produit, il faut calculer le discriminant et vérifier si celui-ci est un carré ou non. Il est donc souhaitable de faire un peu plus de travail en amont afin que le voyage soit ensuite plus tranquille.

On considère un nombre $x$. On multiplie d’abord chaque côté par $8(k-2)$ puis on complète le carré : $$\begin{array}{rl}x& =\frac{(k-2)n^2-(k-4)n}{2}\\ \\ 8(k-2)x& =\frac{8(k-2{)}^2{n}^2-8(k-2)(k-4)n}{2}\\ \\ 8(k-2)x& =4(k-2)n^2-4(k-4)(k-2)n\\ \\ 8(k-2)x& =(2(k-2)n{)}^2-4(k-4)(k-2)n+(k-4{)}^2-(k-4{)}^2\\ \\ 8(k-2)x& ={(2(k-2)n–(k-4))}^2-(k-4{)}^2\\ \\ 8(k-2)x+(k-4{)}^2& ={(2(k-2)n–(k-4))}^2\end{array}$$

À quoi tout cela rime ? Si $x$ est un nombre $k-$gonal, alors $8(k-2)x+(k-4{)}^2$ est un carré parfait. On peut aussi trouver son rang facilement. En gardant la racine positive à la deuxième étape, on obtient $$\begin{array}{rl}8(k-2)x+(k-4{)}^2& ={(2(k-2)n-(k-4))}^2\\ \\ \sqrt{8(k-2)x+(k-4{)}^2}& =2(k-2)n-(k-4)\\ \\ \sqrt{8(k-2)x+(k-4{)}^2}+(k-4)& =2(k-2)n\\ \\ \frac{\sqrt{8(k-2)x+(k-4{)}^2}+(k-4)}{2(k-2)}& =n\end{array}$$

Pour terminer, deux derniers exemples. Le nombre $1001$ est-il pentagonal ? Je le multiplie par $8(k-2)=8(5-2)=8(3)=24$ et j’ajoute $(k-4{)}^2=(5-4{)}^2=1^2=1$.$$24(1001)+1=24024+1=24025$$Est-ce que $24025$ est un nombre carré ? Oui ! $$24025={155}^2$$Cela veut dire que $1001$ est un nombre pentagonal. Pour trouver le rang, j’ajoute $k-4=5-4=1$ et je divise par $2(k-2)=2(5-2)=2(3)=6$$$\frac{155+1}{6}=\frac{156}{6}=26$$Ainsi, $1001$ est le ${26}^{\text{e}}$ nombre pentagonal.

Le nombre $1125$ est-il un nombre hexagonal ? Je le multiple par $8(k-2)=8(6-2)=8(4)=32$ et j’ajoute $(k-4{)}^2=(6-4{)}^2=2^2=4$.$$32(1125)+4=36000+4=36004$$Ce nombre est-il un carré ? Puisque ${189}^2=35721$ et ${190}^2=36100$ et que $35721<36004<36100$, non, ce n’est pas un carré ! Ainsi, le nombre $1125$ n’est pas un nombre hexagonal.

Référence :

NELSON, Roger B., Nuggets of Number Theory : A visual Approach, MAA Press 2010