Un homme de principe

Le principe de Cavalieri (ou méthode des indivisibles) est le suivant : si les figures planes déterminées par les intersections de deux solides avec tout plan parallèle à un plan fixe donné ont la même aire, alors les deux solides ont le même volume.

Pour appliquer le principe, il ne suffit donc pas d’avoir des solides de même volume : ces solides doivent aussi être orientés correctement. On comprend aussi qu’une fois orientés, les solides doivent nécessairement avoir la même hauteur. Enfin, il est évidemment possible de trouver des solides de même volume mais dont les coupes transversales n’ont pas la même aire, qu’importe l’orientation des solides.

Le principe est nommé en l’honneur de Bonaventura Cavalieri (1598-1647) qui l’énonce et tente d’en fournir une preuve. Le principe en soi n’est cependant pas nouveau à cette époque. Archimède utilise une idée semblable 16 siècles auparavant pour établir des relations entre les volumes de différents solides. Et dans ses écrits il crédite Exodus et Democrite pour l’utilisation de cette méthode, bien avant, dans leur découverte du volume du cône. Liu Hui, au 3^ième siècle, utilise le principe de Cavalieri pour trouver le volume du cylindre.

Au 17^ième siècle, Cavalieri redécouvre le principe et l’utilise pour trouver lui aussi des expressions pour le volume de différents solides. Cependant, contrairement à ceux qui le précèdent, il s’intéresse également au principe de manière plus générale, pour des solides quelconques. Il essaie aussi de fournir une preuve rigoureuse du principe en utilisant la méthode d’exhaustion d’Archimède. Plus tard, le développement du calcul intégral permet aux mathématiciens d’accéder à cette rigueur.

L’idée fondamentale du principe de Cavalieri n’est pas de calculer directement des volumes, mais de les comparer : l’astuce consiste à trouver quels sont les solides appropriés à comparer.

Le volume de la boule

Une des plus belles applications du principe est la suivante : trouver une expression pour le volume de la boule. Pour ce faire, on utilise un solide qui possède des coupes transversales équivalentes aux coupes de la boule : bien évidemment, ce solide est plus facile à mesurer, plus « simple », que la boule elle-même.

On considère une boule de rayon 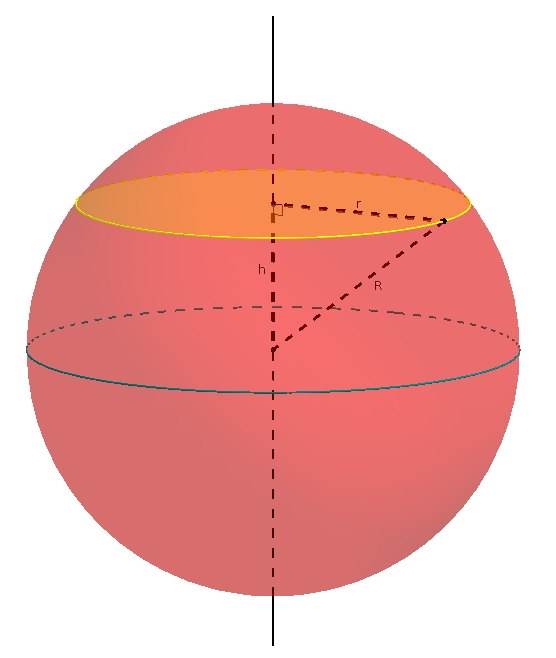$R$ et on fixe un équateur et le plan qui supporte cet équateur. On coupe ensuite la boule avec un plan parallèle au plan qui supporte l’équateur et à une hauteur $h$ de celui-ci. L’intersection du plan et de la boule est un disque de rayon $r$ (en jaune sur la figure). Lorsque $h$ vaut zéro, le disque est ce qu’on appelle un grand disque de la boule : un disque qui passe par son centre et son rayon à ce moment est $R$. Puis, dans l’hémisphère nord, lorsque $h$ augmente, le rayon du disque diminue, jusqu’à ce que le disque dégénère en un seul point lorsque $h=R$. Par symétrie, on observe un phénomène semblable dans l’hémisphère sud.L’aire de ce disque est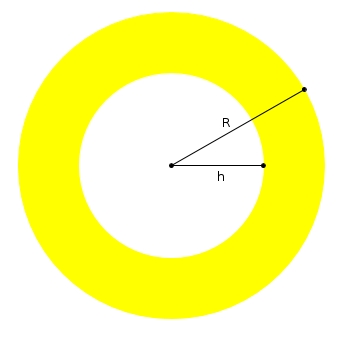 $$A=\pi r^2$$De quelle manière le rayon $r$ du disque diminue-t-il en fonction de la hauteur $h$ ? On considère le triangle rectangle dont les cathètes mesurent $r$ et $h$ et l’hypoténuse $R$, le rayon de la boule. Avec Pythagore, on trouve $$r^2+h^2=R^2$$ ce qui donne en soustrayant $h^2$ $$r^2=R^2-h^2$$En substituant, on peut donc exprimer l’aire du disque comme $$A=\pi (R^2-h^2)$$Cette expression algébrique peut être interprétée géométriquement de belle manière : elle correspond aussi à l’aire de la région comprise entre deux disques de rayon $R$ et $h$. Cette région s’appelle une couronne (annulus en latin).

L’aire de cette couronne est $A=\pi (R^2-h^2)$ 

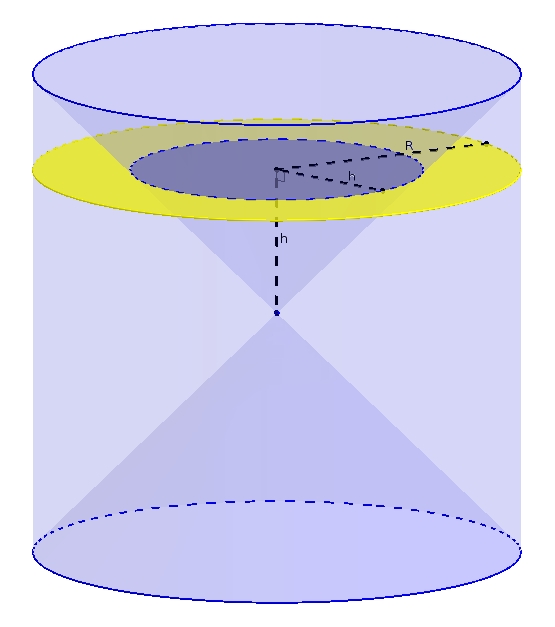
L’extraordinaire coup de génie consiste à trouver un solide qui possède de telles couronnes comme coupes transversales : un cylindre duquel on a enlevé deux cônes.

La hauteur de ce cylindre est $2R$, son rayon est $R$. La hauteur de chaque cône est donc \(R\) et leur rayon est le même que celui du cylindre. On sait que le cône occupe le tiers du cylindre de même base et de même hauteur, c’est donc dire que le solide qui possède le même volume que la boule correspond au $\frac{2}{3}$ du cylindre.

Ainsi, on a $$V_{\text{boule}}=\frac{2}{3}\cdot V_{\text{cylindre}}$$c’est-à-dire $$V_{\text{boule}}=\frac{2}{3}(\pi \cdot R^2\cdot 2R)$$ce qui est équivalent à la formule bien connue $$V_{boule}=\frac{4\pi R^3}{3}$$

Référence : Paul Lockhart (2012), Measurement

Tom Apostol and Mamikon Mnatsakanian (2013),  New Horizons in Geometry