Une méthode pour les remplacer toutes…

Un Anneau pour les gouverner tous ^[1]

Les élèves de quatrième et cinquième secondaire ont régulièrement à trouver l’équation d’une fonction quadratique, que cela soit sous la forme générale, $$f(x)=a{x}^2+bx+c$$la forme canonique, $$f(x)=a(x-h{)}^2+k$$ou, dans certains cas, la forme factorisée, $$f(x)=a(x-x_1)(x-x_2)$$Il est normal de choisir la forme selon les données fournies dans le problème. Si on connaît les deux zéros de la fonction et un autre couple appartenant à la fonction, la forme factorisée est préférée. Si on connaît le couple qui contient l’extrémum de la fonction et un autre couple appartenant à la fonction, c’est la forme canonique qui est préférée.

Petit aparté : il y a souvent une confusion entre la fonction et ses représentations, en particulier sa représentation graphique. La représentation graphique d’une fonction quadratique est une parabole. Ainsi, « connaître le couple qui contient l’extrémum de la fonction et un autre couple appartenant à la fonction », revient à « connaître les coordonnées du sommet de la parabole qui représente la fonction quadratique dans le plan cartésien ainsi que les coordonnées d’un autre point sur cette parabole ». Un petit abus de langage plus tard et on laisse tomber « qui représente la fonction quadratique ». Un autre plus tard et on obtient : « le sommet de la fonction quadratique ». Vous m’excuserez si jamais je me rends coupable de tels abus de langage plus loin dans le texte.

Il existe aussi d’autres cas, dans lesquels on doit parfois résoudre des systèmes d’équations à deux inconnues. Par exemple, si on connaît deux couples possédant la même ordonnée et un autre couple appartenant à la fonction, on peut déduire l’abscisse $h$ du sommet de la parabole et utiliser la forme canonique ; on résout ensuite le système d’équations linéaires à deux variables pour trouver les valeurs de $a$ et $k$.

Tous ces cas sont couverts dans les manuels ou les ressources en ligne, par exemple ici.

Absent de cette liste est le cas où on connaît trois couples quelconques appartenant à la fonction : quelconque voulant dire ici qu’on ne connaît ni les zéros, ni l’ordonnée à l’origine, ni l’extrémum, etc. Dans ce cas, il faut résoudre un système d’équations à trois inconnues $a$, $b$ et $c$ en utilisant la forme générale. Puisque de tels systèmes à trois inconnues ne sont pas au programme de quatrième ni de cinquième secondaire, ce cas n’est habituellement pas abordé en classe. 

 

Un exemple

Quelle est l’équation de la fonction quadratique possédant les couples suivants : $$(2,-10)(5,-16)(11,80)$$

On remplace trois fois dans $f(x)=a{x}^2+bx+c$ : $$\begin{array}{rl}-10& =a(2{)}^2+b(2)+c\\ \\ -16& =a(5{)}^2+b(5)+c\\ \\ 80& =a(11{)}^2+b(11)+c\end{array}$$ce qui fait $$\begin{array}{rl}-10& =4a+2b+c\\ \\ -16& =25a+5b+c\\ \\ 80& =121a+11b+c\end{array}$$L’astuce, puisque le coefficient de $c$ et $1$ dans chaque équation, est de soustraire l’une des équations aux deux autres. Par exemple, si on soustrait la première aux deux autres, on obtient $$\begin{array}{rl}-10& =4a+2b+c\\ \\ -6& =21a+3b\\ \\ 90& =117a+9b\end{array}$$On se concentre ensuite sur les deux dernières équations. Dans ce cas particulier, si on divise la première par $3$ et la deuxième par $9$, on obtient $$\begin{array}{rl}-2& =7a+b\\ \\ 10& =13a+b\end{array}$$Les coefficients de $b$ étant tous les deux $1$, soustraire la première à la deuxième nous permet d’obtenir la valeur de $a$ : $$12=6a$$ et donc $$2=a$$On remplace ensuite dans l’une ou l’autre des équations pour trouver la valeur de $b$ : $$-2=7(2)+b$$ ce qui fait $$-16=b$$ ou $$10=13(2)+b$$ ce qui fait aussi, sans surprise, $$-16=b$$Enfin, on utilise l’une des équations de départ et on calcule $$\begin{array}{rl}-10& =4(2)+2(-16)+c\\ \\ -10& =8+(-32)+c\end{array}$$pour obtenir $$c=14$$L’équation est donc $$f(x)=2x^2-16x+14$$

Voilà donc pour la postérité ! L’utilisation des matrices, aux niveaux supérieurs, allège bien sûr la tâche et simplifie l’écriture, mais il n’en reste pas moins que l’exercice est un peu fastidieux.

La méthode

Pourtant, nul besoin de résoudre de tels systèmes à plusieurs inconnues. À la rigueur, nul besoin, même, des autres cas. En effet, il suffit simplement… d’écrire l’équation. Directement. Ah oui ? 

Reprenons. 

Quelle est l’équation de la fonction quadratique possédant les couples suivants : $$(2,-10)(5,-16)(11,80)$$

Puisqu’il s’agit d’une fonction quadratique, son équation peut être exprimée avec un polynôme du deuxième degré. Celui-ci peut être le résultat d’un produit de deux facteurs du premier degré ou d’une somme de produits d’au plus deux facteurs du premier degré. Soit. On peut construire l’équation de la manière suivante. On cherchera trois termes. $$f(x)=\dots +\dots +\dots$$D’abord, on écrit $$f(x)=?\cdot \frac{(x-5)(x-11)}{?}+?\cdot \frac{(x-2)(x-11)}{?}+?\cdot \frac{(x-2)(x-5)}{?}$$Il est évident que si $x=2$, les deux derniers termes sont nuls, seul le premier terme subsiste. De manière analogue, si $x=5$, ce sont le premier et le dernier terme qui sont nuls, mais pas le deuxième, alors que si $x=11$, ce sont les deux premiers termes qui sont nuls, mais pas le dernier ! On complète le premier terme de cette manière : si $x$ prend la valeur de $2$, on voudrait que le premier terme non-nul soit $-10$. Or, $$2-5=-3$$ et $$2-11=-9$$Ainsi, le premier terme sera $$f(x)=-10\cdot \frac{(x-5)(x-11)}{(-3)(-9)}+?\cdot \frac{(x-2)(x-11)}{?}+?\cdot \frac{(x-2)(x-5)}{?}$$Je construis le deuxième et le troisième terme de la même manière. Si $x=5$, on voudrait que le deuxième terme soit $-16$. Or, $$5-2=3$$ et $$5-11=-6$$On obtient $$f(x)=-10\cdot \frac{(x-5)(x-11)}{(-3)(-9)}+(-16)\cdot \frac{(x-2)(x-11)}{(3)(-6)}+?\cdot \frac{(x-2)(x-5)}{?}$$Enfin, si $x=11$, on voudrait que le troisième terme soit $80$. Sachant que $$11-2=9$$ et $$11-5=6$$ on obtient $$f(x)=-10\cdot \frac{(x-5)(x-11)}{(-3)(-9)}+(-16)\cdot \frac{(x-2)(x-11)}{(3)(-6)}+80\cdot \frac{(x-2)(x-5)}{(9)(6)}$$Voilà ! C’est tout ! Cela nous assure que $$\begin{array}{rl}f(2)& =-10\cdot \frac{(2-5)(2-11)}{(-3)(-9)}+(-16)\cdot \frac{(2-2)(2-11)}{(3)(-6)}+80\cdot \frac{(2-2)(2-5)}{(9)(6)}\\ \\ & =-10\cdot \frac{(-3)(-9)}{(-3)(-9)}+0+0\\ \\ & =-10\cdot 1+0+0\\ \\ & =-10\\ \\ \\ \\ f(5)& =-10\cdot \frac{(5-5)(5-11)}{(-3)(-9)}+(-16)\cdot \frac{(5-2)(5-11)}{(3)(-6)}+80\cdot \frac{(5-2)(5-5)}{(9)(6)}\\ \\ & =0+(-16)\cdot \frac{(3)(-6)}{(3)(-6)}+0\\ \\ & =0+(-16)\cdot 1+0\\ \\ & =-16\\ \\ \\ \\ f(11)& =-10\cdot \frac{(11-5)(11-11)}{(-3)(-9)}+(-16)\cdot \frac{(11-2)(11-11)}{(3)(-6)}+80\cdot \frac{(11-2)(11-5)}{(9)(6)}\\ \\ & =0+0+80\cdot \frac{(9)(6)}{(9)(6)}\\ \\ & =0+0+80\cdot 1\\ \\ & =80\end{array}$$et que le résultat sera un polynôme du deuxième degré. De petits calculs additionnels nous permettent d’écrire : $$\begin{array}{rl}f(x)& =-10\cdot \frac{(x-5)(x-11)}{(-3)(-9)}+(-16)\cdot \frac{(x-2)(x-11)}{(3)(-6)}+80\cdot \frac{(x-2)(x-5)}{(9)(6)}\\ \\ & =-10\cdot \frac{(x-5)(x-11)}{27}+(-16)\cdot \frac{(x-2)(x-11)}{-18}+80\cdot \frac{(x-2)(x-5)}{54}\\ \\ & =-\frac{10}{27}(x-5)(x-11)+\frac{8}{9}(x-2)(x-11)+\frac{40}{27}(x-2)(x-5)\end{array}$$

D’ailleurs, $$\begin{array}{rl}f(x)& =-\frac{10}{27}(x-5)(x-11)+\frac{8}{9}(x-2)(x-11)+\frac{40}{27}(x-2)(x-5)\\ \\ \\ & =-\frac{10}{27}(x^2-16x+55)+\frac{24}{27}(x^2-13x+22)+\frac{40}{27}(x^2-7x+10)\\ \\ \\ & =\frac{-10x^2+160x-550+24x^2-312x+528+40x^2-280x+400}{27}\\ \\ \\ & =\frac{54x^2-432x+378}{27}\\ \\ \\ & =2x^2-16x+14\end{array}$$ce qu’on avait trouvé plus tôt. Dans certains problèmes, il n’est souvent pas nécessaire d’effectuer les dernières étapes afin d’obtenir une des trois formes mentionnées au début du billet (ici la forme générale) : parfois on cherche simplement la valeur de la fonction pour certaines valeurs de $x$. Il suffit alors de remplacer et calculer.

En général, pour la fonction quadratique …

Ainsi, si les couples $$(x_1,y_1)(x_2,y_2)(x_3,y_3)$$appartiennent à la fonction quadratique $f$, alors $$f(x)=\frac{y_1(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}+\frac{y_2(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}+\frac{y_3(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)}$$ 

… et peu importe le degré

Sans surprise, la méthode s’applique sans grande modification aux fonctions polynomiales de degrés quelconques. Elle fonctionne aussi bien pour les fonctions affines que pour les fonction polynomiales de degrés supérieurs à deux.

Un exemple (bis) : une fonction cubique

Quelle est l’équation de la fonction cubique possédant les couples 

$$(-3,-1)(-2,2)(1,-5)(3,37)?$$

Un petit instant de réflexion nous permet d’écrire directement

$$\begin{array}{rl}f(x)=& \phantom{+}(-1)\cdot \frac{(x+2)(x-1)(x-3)}{(-1)(-4)(-6)}\\ \\ & +2\cdot \frac{(x+3)(x-1)(x-3)}{(1)(-3)(-5)}\\ \\ & +(-5)\cdot \frac{(x+3)(x+2)(x-3)}{(4)(3)(-2)}\\ \\ & +37\cdot \frac{(x+3)(x+2)(x-1)}{(6)(5)(2)}\end{array}$$

Génial non ? 

À l’instar de ce qu’on a fait plus tôt avec la fonction quadratique, on trouve l’équation d’une fonction cubique possédant les couples $(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$ et $(x_4,y_4)$. On obtient $$\begin{array}{rl}f(x)=& \phantom{+}\frac{y_1(x-x_2)(x-x_3)(x-x_4)}{(x_1-x_2)(x_1-x_3)(x_1-x_4)}\\ \\ & +\frac{y_2(x-x_1)(x-x_3)(x-x_4)}{(x_2-x_1)(x_2-x_3)(x_2-x_4)}\\ \\ & +\frac{y_3(x-x_1)(x-x_2)(x-x_4)}{(x_3-x_1)(x_3-x_2)(x_3-x_4)}\\ \\ & +\frac{y_4(x-x_1)(x-x_2)(x-x_3)}{(x_4-x_1)(x_4-x_2)(x_4-x_3)}\end{array}$$

La fonction affine

En utilisant la même méthode, on peut trouver l’équation de la fonction affine possédant les couples $(x_1,y_1)$ et $(x_2,y_2)$.

$$f(x)=\frac{y_1(x-x_2)}{(x_1-x_2)}+\frac{y_2(x-x_1)}{(x_2-x_1)}$$ce qui est un peu différent (mais parfaitement équivalent) à la forme trouvée en utilisant le taux de variation $a=\frac{y_2-y_1}{x_2-x_1}$ et en résolvant ensuite pour trouver la valeur de $b$ dans $$f(x)=ax+b$$

Enfin… toutes ! 

Waring, Euler et Lagrange ^[2]

Il est possible de généraliser davantage. On considère une fonction polynomiale de degré $n$ définie par $n+1$ couples $(x_i,y_i)$. Encore une fois, un petit moment de réflexion nous permet de déduire que $$f(x)=\sum _{i=1}^{n+1}(y_i\cdot \prod _{\begin{array}{c}j=1\\ j\ne i\end{array}}^{n+1}\frac{x-x_j}{x_i-x_j})$$ou, si on veut éviter la notation $\prod$, $$f(x)=\sum _{i=1}^{n+1}\frac{y_i(x-x_1)(x-x_2)\cdot \dots \cdot (x-x_{i-1})(x-x_{i+1})\cdot \dots \cdot (x-x_{n+1})}{(x_i-x_1)(x_i-x_2)\cdot \dots \cdot (x_i-x_{i-1})(x_i-x_{i+1})\cdot \dots \cdot (x_i-x_{n+1})}$$ou, encore, si on veut en plus éviter la notation $\sum$, $$\begin{array}{rl}f(x)=& \phantom{+}\frac{y_1(x-x_2)(x-x_3)\cdot \dots \cdot (x-x_{n+1})}{(x_1-x_2)(x_1-x_3)\cdot \dots \cdot (x_1-x_{n+1})}\\ \\ & +\frac{y_2(x-x_1)(x-x_3)\cdot \dots \cdot (x-x_{n+1})}{(x_2-x_1)(x_2-x_3)\cdot \dots \cdot (x_2-x_{n+1})}\\ \\ & +\dots \\ \\ & +\frac{y_i(x-x_1)(x-x_2)\cdot \dots \cdot (x-x_{i-1})(x-x_{i+1})\cdot \dots \cdot (x-x_{n+1})}{(x_i-x_1)(x_i-x_2)\cdot \dots \cdot (x_i-x_{i-1})(x_i-x_{i+1})\cdot \dots \cdot (x_i-x_{n+1})}\\ \\ & +\dots \\ \\ & +\frac{y_{n+1}(x_{n+1}-x_1)(x_{n+1}-x_2)\cdot \dots \cdot (x_{n+1}-x_n)}{(x_{n+1}-x_1)(x_{n+1}-x_2)\cdot \dots \cdot (x_{n+1}-x_n)}\end{array}$$Le lecteur initié aura reconnu qu’il s’agit d’un polynôme de Lagrange.

Un petit problème

En terminant, pour s’amuser un peu, tout cette discussion m’a fait pensé à ce petit problème de Jean-Paul Delahaye, paru dans le magazine Accromath, Volume 13.2 – été-automne 2018 ^[3]. 

Considérons l’équation suivante : 

$$\frac{(x-a)(x-b)}{(c-a)(c-b)}+\frac{(x-b)(x-c)}{(a-b)(a-c)}+\frac{(x-a)(x-c)}{(b-a)(b-c)}=1$$

Le membre de gauche est une somme de termes qui sont eux-mêmes des produits de deux facteurs du premier degré. Si on développe, on devrait obtenir un trinôme du deuxième degré. Cette équation ne devrait avoir au maximum que deux solutions. Pourtant, lorsque $x=a$, on a $$\begin{array}{rl}\frac{(a-a)(a-b)}{(c-a)(c-b)}+\frac{(a-b)(a-c)}{(a-b)(a-c)}+\frac{(a-a)(a-c)}{(b-a)(b-c)}& =1\\ \\ 0+1+0& =1\\ \\ 1& =1\end{array}$$De la même manière, si $x=b$, $$\begin{array}{rl}\frac{(b-a)(b-b)}{(c-a)(c-b)}+\frac{(b-b)(b-c)}{(a-b)(a-c)}+\frac{(b-a)(b-c)}{(b-a)(b-c)}& =1\\ \\ 0+0+1& =1\\ \\ 1& =1\end{array}$$et si $x=c$, $$\begin{array}{rl}\frac{(c-a)(c-b)}{(c-a)(c-b)}+\frac{(c-b)(c-c)}{(a-b)(a-c)}+\frac{(c-a)(c-c)}{(b-a)(b-c)}& =1\\ \\ 1+0+0& =1\\ \\ 1& =1\end{array}$$Il y a trois solutions : $a$, $b$ et $c$ ! Comment cela est-il possible ? 

Annexe

Autre petit aparté : l’étude des fonctions, en particulier des fonctions quadratiques, n’est pas toujours facile pour les élèves. Certains se sentent rassurés lorsqu’ils utilisent des méthodes familières, à la rigueur routinières. D’autres préfèrent utiliser des formules.

Exemple typique :

Tracer la parabole d’équation $$y=2(x-8)(x+4)+54$$

Comme la forme de l’équation ne correspond à aucune des trois mentionnées ci-dessus, l’approche privilégiée dans les manuels serait de transformer l’équation en l’une des trois formes, de préférence la forme canonique, pour tracer la parabole. On peut y arriver en effectuant quelques étapes algébriques. D’abord, $$\begin{array}{rl}y& =2(x-8)(x-4)+54\\ \\ & =2(x^2-8x+4x-32)+54\\ \\ & =2(x^2-4x-32)+54\end{array}$$Il est à noter que plusieurs élèves continueraient ici à développer jusqu’à la forme générale. C’est inutile. On complète le carré : $$\begin{array}{rl}y& =2(x^2-4x+4-4-32)+54\\ \\ & =2((x-2{)}^2-4-32)+54\\ \\ & =2((x-2{)}^2-36)+54\\ \\ & =2(x-2{)}^2-72+54\\ \\ & =2(x-2{)}^2-18\end{array}$$

Le sommet de la parabole est donc en $(2,-18)$ et la parabole est ouverte vers le haut car $a>0$.  On peut ensuite calculer les zéros et l’ordonnée à l’origine pour un peu plus de précision.

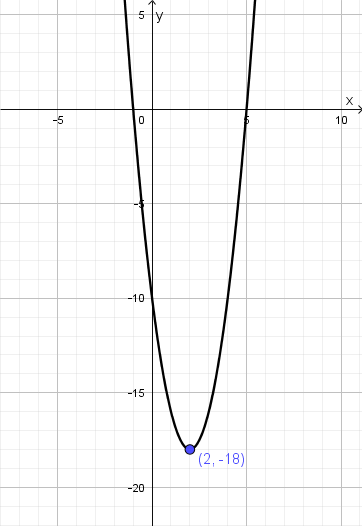
Alternative : Nul besoin de compléter le carré ! ^[4] Clairement, on voit en examinant l’équation sous cette forme$$y=2(x-8)(x+4)+54$$que $$f(8)=f(-4)=54$$Puisque la parabole possède un axe de symétrie qui passe par son sommet, les points $(8,54)$ et $(-4,54)$ sont situés à la même distance de part et d’autre de cet axe. On peut déduire l’abscisse du sommet est $$\frac{8+(-4)}{2}=2$$L’ordonnée du sommet est donnée par $$\begin{array}{rl}y& =2(2-8)(2+4)+54\\ \\ & =2(-6)(6)+54\\ \\ & =-72+54\\ \\ & =-18\end{array}$$La parabole a pour sommet $(2,-18)$ et elle est ouverte vers le haut ; en prime, on sait qu’elle passe par $(8,54)$ et $(-4,54)$. On peut calculer l’ordonnée à l’origine facilement pour plus de précision.

[1] ^{https://commons.wikimedia.org/wiki/File:One_Ring_Blender_Render.png}

[2] ^{https://commons.wikimedia.org/wiki/File:%D0%9B%D0%B0%D0%B3%D1%80%D0%B0%D0%BD%D0%B6.jpg}

[3] Vous pouvez trouver l’original ici : https://accromath.uqam.ca/wp-content/uploads/2018/09/Paradoxes_13_2.pdf

[4] La complétion du carré en fait trembler plusieurs. Il est pourtant essentiel qu’ils la maîtrisent pour la suite. Le but n’est pas d’éviter à tout prix la complétion du carré, mais d’encourager la compréhension de ce qu’implique l’équation, peu importe la forme.