« Volumetric » « area »

Les compagnies de livraison ont des règlements très particuliers pour les dimensions des colis qu’elles acceptent. Elles se basent toutes sur une variation d’un même concept (que la compagnie anglaise myHermes avait baptisé volumetric area, avec beaucoup de sérieux, bien qu’on ne parle ni de volume, ni d’aire, mais bien d’une longueur. myHermes a depuis retiré le terme de leur site.) On considère à titre d’exemple les restrictions de l’une de ces compagnies, certainement une des plus connues, mais qu’on gardera néanmoins anonyme.

UPS ? Postes Canada ? USPS ? Mystère !

Elle définit le plus long côté du colis comme la “longueur” du colis.

• La longueur du colis ne doit pas dépasser 108 po.
• Si on fait la somme des mesures des deux plus petits côtés, qu’on double cette somme (on obtient « le tour de taille ») et qu’on ajoute ensuite la mesure de la longueur, le total (la somme du « tour de taille » et de la longueur) doit être inférieur ou égal à 165 po.

On peut traduire ces contraintes de manière formelle. On considère le prisme droit à base rectangulaire suivant, avec $x\le y\le z$.

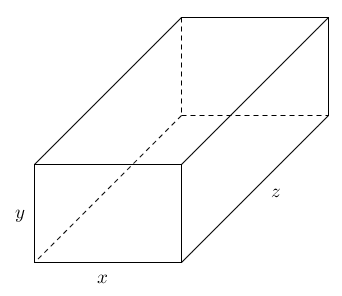
On a donc $$z\le 108$$ et $$2(x+y)+z\le 165$$La question est la suivante : quelles sont les dimensions d’une boîte qui satisfasse ces contraintes et qui possède le volume maximal (et quel est ce volume) ?

_{Divulgâcheur : ce n’est pas un cube !}

The inégalité

Bien que cela soit un calcul d’optimisation (on maximise le volume sous certaines contraintes), on peut s’en tirer, avec un peu d’astuce et notre inégalité des moyennes arithmétique et géométrique, sans calcul différentiel (rien de personnel, calcul différentiel). L’inégalité pour 3 nombres stipule que $$\sqrt[3]{abc}\le \frac{a+b+c}{3}$$ou, de manière équivalente, $$abc\le {\left(\frac{a+b+c}{3}\right)}^3$$Dans notre cas, on a, d’une part $$2x+2y+z\le 165$$et, d’autre par,$$V=xyz$$On cherche bien sûr à maximiser $V$, le volume en po³. Il suffit de faire apparaître $2x$ et $2y$ dans le calcul de $V$$$\begin{array}{rl}V& =x\cdot y\cdot z\\ \\ & =\frac{2x}{2}\cdot \frac{2y}{2}\cdot z\\ \\ & =\frac{1}{4}(2x\cdot 2y\cdot z)\end{array}$$puis d’appliquer l’inégalité$$\begin{array}{rl}V& =\frac{1}{4}(2x\cdot 2y\cdot z)\\ \\ & \le \frac{1}{4}{\left(\frac{2x+2y+z}{3}\right)}^3\end{array}$$En utilisant $$2x+2y+z=165$$on obtient$$V\le \frac{1}{4}{\left(\frac{2x+2y+z}{3}\right)}^3=\frac{1}{4}{\left(\frac{165}{3}\right)}^3=\frac{166375}{4}=41593,75$$Le volume maximal est donc 41 593,75 po³ et ce maximum est atteint lorsqu’on a $2x=2y=z$. Ainsi, la boîte a pour dimensions$$27,5\times 27,5\times 55$$ce qui correspond à deux cubes dont les arêtes mesurent 27,5 po, collés l’un contre l’autre.