La somme des inverses des entiers naturels non-nuls (la série harmonique) tend vers l’infini (voir ici pour la preuve de Nicole Oresme). On dit que la série est divergente. Ainsi, \[\lim_{n\to \infty}\sum_{i=1}^{n}\frac{1}{i}=\infty\]Le grand Euler a montré (une première fois à vingt-huit ans dans une preuve particulièrement eulérienne en 1735, puis à nouveau avec une preuve plus rigoureuse en 1741) que la somme des inverses des carrés des entiers naturels non-nuls converge vers une valeur, aussi surprenante soit-elle d’ailleurs, cette valeur. C’est le problème de Bâle. On écrit \[\lim_{n\to \infty}\sum_{i=1}^{n}\frac{1}{i^{2}}= \frac{\pi^{2}}{6}\]Deux séries intimement liées, l’une divergente, l’autre convergente. Avec cette malice toute mathématique, on décide d’accoler un carré de côté \(1\) et d’aire \(1\) à un carré de côté \(\frac{1}{2}\) et d’aire \(\frac{1}{4}\). On accole ensuite un carré de côté \(\frac{1}{3}\) et d’aire \(\frac{1}{9}\). Puis on accole un carré de côté \(\frac{1}{4}\) et d’aire \(\frac{1}{16}\). On continue le processus aussi longtemps qu’on le souhaite tel qu’illustré dans l’image ci-dessous …
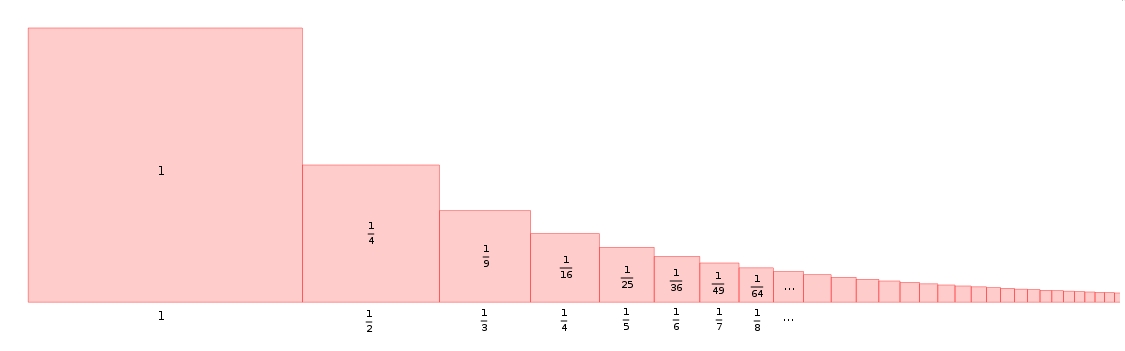
Et il se trouve qu’en continuant le processus aussi longtemps que désiré, la mesure d’un côté de cette figure, le côté inférieur, tend vers l’infini (c’est la série harmonique) alors que son aire tend vers un nombre bien fini, bien tangible (c’est le problème de Bâle).
C’est aussi le problème un peu gênant du pauvre peintre qui a besoin d’une quantité finie de peinture pour peindre l’intérieur des carrés mais d’une quantité infinie de peinture pour seulement en tracer les contours.
Référence : A harmonic serie paradox via Let’s play math